2018-2019学年安徽省合肥四十五中九年级(上)期中数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年安徽省合肥四十五中九年级(上)期中数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 07:30:08 | ||
图片预览



文档简介
2018-2019学年安徽省合肥四十五中九年级(上)期中数学试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.将二次函数的图象向左平移1个单位,则平移后的二次函数的解析式为
A. B. C. D.
2.如果反比例函数的图象经过点,,则的值是
A. B. C. D.
3.已知,则下列比例式成立的是
A. B. C. D.
4.若△,相似比为,则与△的面积的比为
A. B. C. D.
5.二次函数,若,则其图象经过点
A. B. C. D.
6.如图,中,是中线,,,则线段的长是
A.8 B. C.12 D.
7.如图,平面直角坐标系中,点是轴上任意一点,平行于轴,分别交、的图象于、两点,若的面积为2,则值为
A. B.1 C. D.
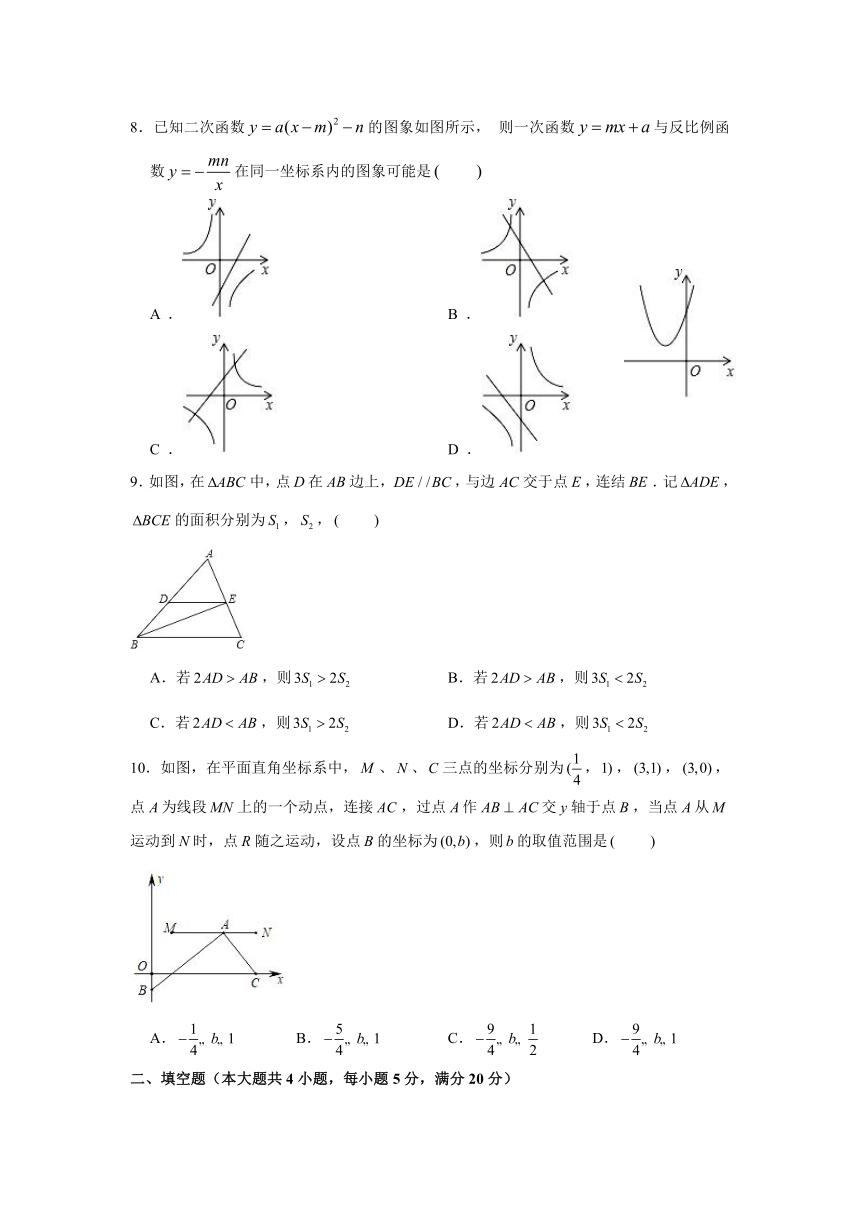
8.已知二次函数的图象如图所示, 则一次函数与反比例函数在同一坐标系内的图象可能是
A . B .
C . D .
9.如图,在中,点在边上,,与边交于点,连结.记,的面积分别为,,
A.若,则 B.若,则
C.若,则 D.若,则
10.如图,在平面直角坐标系中,、、三点的坐标分别为,,,,点为线段上的一个动点,连接,过点作交轴于点,当点从运动到时,点随之运动,设点的坐标为,则的取值范围是
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,为的黄金分割点,如果的长度为,那么的长度为 .
12.已知点、、在抛物线上,则、、的大小关系是 (用“”联结).
13.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
14.二次函数,若当时,,则当时,函数值的取值范围为 .
三、(本大题共2小题,每小题8分,满分16分)
15.已知抛物线过点.
(1)求的值;
(2)求该抛物线顶点的坐标.
16.如图,已知在中,,,,,.求:四边形的周长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图, 已知是坐标原点,,两点的坐标分别为,.
(1) 以点为位似中心在轴的左侧将放大到两倍, 画出图形;
(2) 分别写出,两点的对应点,的坐标;
(3) 求△的面积 .
18.某施工地在道路拓宽施工时,遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为90米的三角形绿化地,由于马路拓宽绿地被占去了一部分,变成了四边形且,原绿化地一边的长由原来的30米缩短成为18米.求被占去的部分面积有多大?它的周长是多少?
五、(本大题共2小题,每小题10分,满分20分)
19.如图,一次函数和反比例函数交于点与点.
(1)求反比例函数和一次函数的解析式;
(2)求的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.
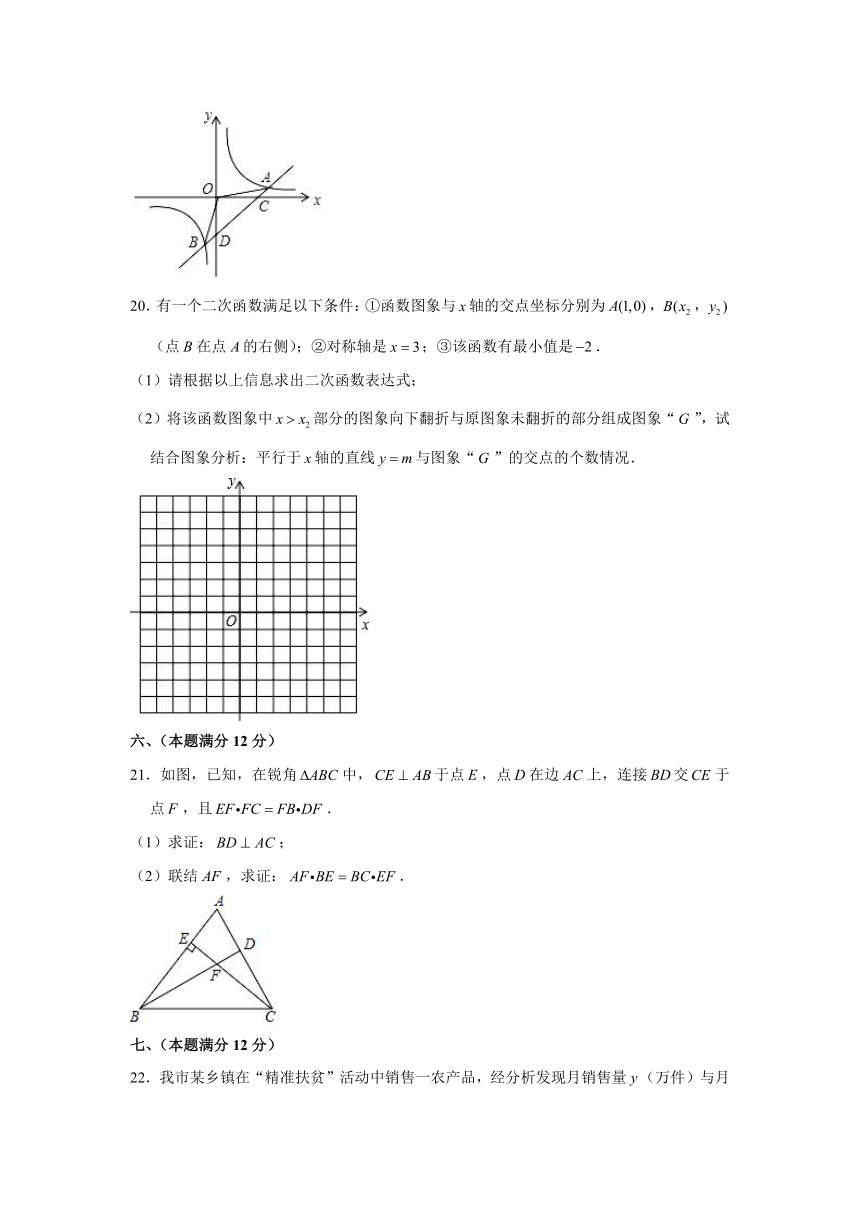
20.有一个二次函数满足以下条件:①函数图象与轴的交点坐标分别为,,(点在点的右侧);②对称轴是;③该函数有最小值是.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象中部分的图象向下翻折与原图象未翻折的部分组成图象“”,试结合图象分析:平行于轴的直线与图象“”的交点的个数情况.
六、(本题满分12分)
21.如图,已知,在锐角中,于点,点在边上,连接交于点,且.
(1)求证:;
(2)联结,求证:.
七、(本题满分12分)
22.我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量(万件)与月份(月的关系为:,每件产品的利润(元与月份(月的关系如下表:
1 2 3 4 5 6 7 8 9 10 11 12
19 18 17 16 15 14 13 12 11 10 10 10
(1)请你根据表格求出每件产品利润(元与月份(月的关系式;
(2)若月利润(万元)当月销售量(万件)当月每件产品的利润(元,求月利润(万元)与月份(月的关系式;
(3)当为何值时,月利润有最大值,最大值为多少?
八、(本题满分14分)
23.我们知道,三角形三个内角平分线的交点叫做三角形的内心,已知点为的内心.
(1)如图1,连接并延长交于点,若,,求的长;
(2)如图2,过点作直线交于点,交于点.
①若,求证:;
②如图3,交于点,若,,求的值.
2018-2019学年安徽省合肥四十五中九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1.将二次函数的图象向左平移1个单位,则平移后的二次函数的解析式为
A. B. C. D.
【解答】解:由题意,得
的图象向左平移1个单位,则平移后的二次函数的解析式为,
故选:.
2.如果反比例函数的图象经过点,,则的值是
A. B. C. D.
【解答】解:反比例函数的图象经过点,,
.
故选:.
3.已知,则下列比例式成立的是
A. B. C. D.
【解答】解:、由得,故本选项正确;
、由得,故本选项错误;
、由得,故本选项错误;
、由 得,故本选项错误.
故选:.
4.若△,相似比为,则与△的面积的比为
A. B. C. D.
【解答】解:△,相似比为,
与△的面积的比为.
故选:.
5.二次函数,若,则其图象经过点
A. B. C. D.
【解答】解:当时,,
而,
时,,
二次函数的图象经过点.
6.如图,中,是中线,,,则线段的长是
A.8 B. C.12 D.
【解答】解:是中线,,
,
,,
,
故选:.
7.如图,平面直角坐标系中,点是轴上任意一点,平行于轴,分别交、的图象于、两点,若的面积为2,则值为
A. B.1 C. D.
【解答】解:连接、,如图,
轴,
,
而,
,
而,
.
故选:.
8.已知二次函数的图象如图所示, 则一次函数与反比例函数在同一坐标系内的图象可能是
A . B .
C . D .
【解答】解:抛物线开口向上,
,
由图可知,,,
,
一次函数的图象过第一、 二、 四象限, 反比例函数分布在第二、 四象限 .
故选:.
9.如图,在中,点在边上,,与边交于点,连结.记,的面积分别为,,
A.若,则 B.若,则
C.若,则 D.若,则
【解答】解:如图,在中,,
,
,
若,即时,,
此时,而.但是不能确定与的大小,
故选项不符合题意,选项不符合题意.
若,即时,,
此时,
故选项不符合题意,选项符合题意.
故选:.
10.如图,在平面直角坐标系中,、、三点的坐标分别为,,,,点为线段上的一个动点,连接,过点作交轴于点,当点从运动到时,点随之运动,设点的坐标为,则的取值范围是
A. B. C. D.
【解答】解:如图,延长交轴于点,则轴.连接.
在与中,
,
,
,
设,则,设,
,
,
,,
时,有最大值,此时,
时,有最小值0,此时,
的取值范围是.
故选:.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,为的黄金分割点,如果的长度为,那么的长度为 .
【解答】解:为的黄金分割点,
,
.
故答案为.
12.已知点、、在抛物线上,则、、的大小关系是 (用“”联结).
【解答】解:抛物线的对称轴为直线,
,
抛物线开口方向向下,
.
故答案为:.
13.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
【解答】解:如图1,四边形是正方形,
,,
设,则,,
,
,,
,
,
,
,
如图2,四边形是正方形,
过作于,交于,
设,
,
,
,
同理得:,
,
,
,
该直角三角形能容纳的正方形边长最大是(步,
故答案为:.
14.二次函数,若当时,,则当时,函数值的取值范围为 .
【解答】解:
△
抛物线的对称轴为,或1时,
当时,
当时,
当时,
当时,函数值的取值范围为
故答案为:.
三、(本大题共2小题,每小题8分,满分16分)
15.已知抛物线过点.
(1)求的值;
(2)求该抛物线顶点的坐标.
【解答】解:(1)把代入得,
解得;
(2)抛物线解析式为
,
所以抛物线的顶点坐标为,.
16.如图,已知在中,,,,,.求:四边形的周长.
【解答】解:,,
四边形是平行四边形,
,,
,
,
,
,
,,即,
四边形的周长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图, 已知是坐标原点,,两点的坐标分别为,.
(1) 以点为位似中心在轴的左侧将放大到两倍, 画出图形;
(2) 分别写出,两点的对应点,的坐标;
(3) 求△的面积 .
【解答】解: (1) 如图;
(2),,
,,
,两点的对应点,的坐标为
,;
(3)
,
.
18.某施工地在道路拓宽施工时,遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为90米的三角形绿化地,由于马路拓宽绿地被占去了一部分,变成了四边形且,原绿化地一边的长由原来的30米缩短成为18米.求被占去的部分面积有多大?它的周长是多少?
【解答】解:由题意可得:,
则,
故,
的长由原来的30米缩短成长18米,
,
即,
解得:,
,
解得:.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,一次函数和反比例函数交于点与点.
(1)求反比例函数和一次函数的解析式;
(2)求的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.
【解答】(1)解:点与点在反比例函数图象上,
,即反比例函数的解析式为,
当时,,即,
点与点在一次函数图象上,
,解得:
一次函数解析式为;
(2)解:对于,当时,,
;
(3)解:由图象可得,当或时,一次函数的值大于反例函数的值.
20.有一个二次函数满足以下条件:①函数图象与轴的交点坐标分别为,,(点在点的右侧);②对称轴是;③该函数有最小值是.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象中部分的图象向下翻折与原图象未翻折的部分组成图象“”,试结合图象分析:平行于轴的直线与图象“”的交点的个数情况.
【解答】解:(1)由上述信息可知该函数图象的顶点坐标为:,
设二次函数的表达式为:.
该函数图象经过点,
,
解得
二次函数解析式为:.
(2)如图所示:
当时,直线与有一个交点;
当时,直线与有两个交点;
当时,直线与有三个交点;
当时,直线与有两个交点;
当时,直线与有一个交点.
六、(本题满分12分)
21.如图,已知,在锐角中,于点,点在边上,连接交于点,且.
(1)求证:;
(2)联结,求证:.
【解答】证明:(1),
.
,
.
.
,
.
.
.
(2),
.
,
.
.
.
.
,
.
,
.
七、(本题满分12分)
22.我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量(万件)与月份(月的关系为:,每件产品的利润(元与月份(月的关系如下表:
1 2 3 4 5 6 7 8 9 10 11 12
19 18 17 16 15 14 13 12 11 10 10 10
(1)请你根据表格求出每件产品利润(元与月份(月的关系式;
(2)若月利润(万元)当月销售量(万件)当月每件产品的利润(元,求月利润(万元)与月份(月的关系式;
(3)当为何值时,月利润有最大值,最大值为多少?
【解答】解;(1)当时,设每件产品利润(元与月份(月的关系式为,
,得,
即当时,每件产品利润(元与月份(月的关系式为,
当时,,
由上可得,;
(2)当时,
,
当时,
,
当时,
,
由上可得,;
(3)当时,,
当时,取得最大值,此时;
当时,,
当时,,
则当时,取得最大值,此时,
由上可得,当为8时,月利润有最大值,最大值144万元.
八、(本题满分14分)
23.我们知道,三角形三个内角平分线的交点叫做三角形的内心,已知点为的内心.
(1)如图1,连接并延长交于点,若,,求的长;
(2)如图2,过点作直线交于点,交于点.
①若,求证:;
②如图3,交于点,若,,求的值.
【解答】解:(1)如图1中,作于.设.
,平分,
,,
在中,,
,,,
,
,,,
在中,,
,
,
.
(2)如图2中,连接、.
是内心,
,
,
,
,
,
,
,
设,,
,
,
,
,
,
,
,
,
.
(3)过点作交的延长线于.
,
,,
,
,
,
.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.将二次函数的图象向左平移1个单位,则平移后的二次函数的解析式为
A. B. C. D.
2.如果反比例函数的图象经过点,,则的值是
A. B. C. D.
3.已知,则下列比例式成立的是
A. B. C. D.
4.若△,相似比为,则与△的面积的比为
A. B. C. D.
5.二次函数,若,则其图象经过点
A. B. C. D.
6.如图,中,是中线,,,则线段的长是
A.8 B. C.12 D.
7.如图,平面直角坐标系中,点是轴上任意一点,平行于轴,分别交、的图象于、两点,若的面积为2,则值为
A. B.1 C. D.
8.已知二次函数的图象如图所示, 则一次函数与反比例函数在同一坐标系内的图象可能是
A . B .
C . D .
9.如图,在中,点在边上,,与边交于点,连结.记,的面积分别为,,
A.若,则 B.若,则
C.若,则 D.若,则
10.如图,在平面直角坐标系中,、、三点的坐标分别为,,,,点为线段上的一个动点,连接,过点作交轴于点,当点从运动到时,点随之运动,设点的坐标为,则的取值范围是
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,为的黄金分割点,如果的长度为,那么的长度为 .
12.已知点、、在抛物线上,则、、的大小关系是 (用“”联结).
13.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
14.二次函数,若当时,,则当时,函数值的取值范围为 .
三、(本大题共2小题,每小题8分,满分16分)
15.已知抛物线过点.
(1)求的值;
(2)求该抛物线顶点的坐标.
16.如图,已知在中,,,,,.求:四边形的周长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图, 已知是坐标原点,,两点的坐标分别为,.
(1) 以点为位似中心在轴的左侧将放大到两倍, 画出图形;
(2) 分别写出,两点的对应点,的坐标;
(3) 求△的面积 .
18.某施工地在道路拓宽施工时,遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为90米的三角形绿化地,由于马路拓宽绿地被占去了一部分,变成了四边形且,原绿化地一边的长由原来的30米缩短成为18米.求被占去的部分面积有多大?它的周长是多少?
五、(本大题共2小题,每小题10分,满分20分)
19.如图,一次函数和反比例函数交于点与点.
(1)求反比例函数和一次函数的解析式;
(2)求的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.
20.有一个二次函数满足以下条件:①函数图象与轴的交点坐标分别为,,(点在点的右侧);②对称轴是;③该函数有最小值是.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象中部分的图象向下翻折与原图象未翻折的部分组成图象“”,试结合图象分析:平行于轴的直线与图象“”的交点的个数情况.
六、(本题满分12分)
21.如图,已知,在锐角中,于点,点在边上,连接交于点,且.
(1)求证:;
(2)联结,求证:.
七、(本题满分12分)
22.我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量(万件)与月份(月的关系为:,每件产品的利润(元与月份(月的关系如下表:
1 2 3 4 5 6 7 8 9 10 11 12
19 18 17 16 15 14 13 12 11 10 10 10
(1)请你根据表格求出每件产品利润(元与月份(月的关系式;
(2)若月利润(万元)当月销售量(万件)当月每件产品的利润(元,求月利润(万元)与月份(月的关系式;
(3)当为何值时,月利润有最大值,最大值为多少?
八、(本题满分14分)
23.我们知道,三角形三个内角平分线的交点叫做三角形的内心,已知点为的内心.
(1)如图1,连接并延长交于点,若,,求的长;
(2)如图2,过点作直线交于点,交于点.
①若,求证:;
②如图3,交于点,若,,求的值.
2018-2019学年安徽省合肥四十五中九年级(上)期中数学试卷
参考答案与试题解析
一、选择题(本大题共10小题,每小题4分,满分40分)
1.将二次函数的图象向左平移1个单位,则平移后的二次函数的解析式为
A. B. C. D.
【解答】解:由题意,得
的图象向左平移1个单位,则平移后的二次函数的解析式为,
故选:.
2.如果反比例函数的图象经过点,,则的值是
A. B. C. D.
【解答】解:反比例函数的图象经过点,,
.
故选:.
3.已知,则下列比例式成立的是
A. B. C. D.
【解答】解:、由得,故本选项正确;
、由得,故本选项错误;
、由得,故本选项错误;
、由 得,故本选项错误.
故选:.
4.若△,相似比为,则与△的面积的比为
A. B. C. D.
【解答】解:△,相似比为,
与△的面积的比为.
故选:.
5.二次函数,若,则其图象经过点
A. B. C. D.
【解答】解:当时,,
而,
时,,
二次函数的图象经过点.
6.如图,中,是中线,,,则线段的长是
A.8 B. C.12 D.
【解答】解:是中线,,
,
,,
,
故选:.
7.如图,平面直角坐标系中,点是轴上任意一点,平行于轴,分别交、的图象于、两点,若的面积为2,则值为
A. B.1 C. D.
【解答】解:连接、,如图,
轴,
,
而,
,
而,
.
故选:.
8.已知二次函数的图象如图所示, 则一次函数与反比例函数在同一坐标系内的图象可能是
A . B .
C . D .
【解答】解:抛物线开口向上,
,
由图可知,,,
,
一次函数的图象过第一、 二、 四象限, 反比例函数分布在第二、 四象限 .
故选:.
9.如图,在中,点在边上,,与边交于点,连结.记,的面积分别为,,
A.若,则 B.若,则
C.若,则 D.若,则
【解答】解:如图,在中,,
,
,
若,即时,,
此时,而.但是不能确定与的大小,
故选项不符合题意,选项不符合题意.
若,即时,,
此时,
故选项不符合题意,选项符合题意.
故选:.
10.如图,在平面直角坐标系中,、、三点的坐标分别为,,,,点为线段上的一个动点,连接,过点作交轴于点,当点从运动到时,点随之运动,设点的坐标为,则的取值范围是
A. B. C. D.
【解答】解:如图,延长交轴于点,则轴.连接.
在与中,
,
,
,
设,则,设,
,
,
,,
时,有最大值,此时,
时,有最小值0,此时,
的取值范围是.
故选:.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,为的黄金分割点,如果的长度为,那么的长度为 .
【解答】解:为的黄金分割点,
,
.
故答案为.
12.已知点、、在抛物线上,则、、的大小关系是 (用“”联结).
【解答】解:抛物线的对称轴为直线,
,
抛物线开口方向向下,
.
故答案为:.
13.《九章算术》是我国古代数学名著,书中有下列问题:“今有勾五步,股十二步,问勾中容方几何?”其意思为:“今有直角三角形,勾(短直角边)长为5步,股(长直角边)长为12步,问该直角三角形能容纳的正方形边长最大是多少步?”该问题的答案是 步.
【解答】解:如图1,四边形是正方形,
,,
设,则,,
,
,,
,
,
,
,
如图2,四边形是正方形,
过作于,交于,
设,
,
,
,
同理得:,
,
,
,
该直角三角形能容纳的正方形边长最大是(步,
故答案为:.
14.二次函数,若当时,,则当时,函数值的取值范围为 .
【解答】解:
△
抛物线的对称轴为,或1时,
当时,
当时,
当时,
当时,函数值的取值范围为
故答案为:.
三、(本大题共2小题,每小题8分,满分16分)
15.已知抛物线过点.
(1)求的值;
(2)求该抛物线顶点的坐标.
【解答】解:(1)把代入得,
解得;
(2)抛物线解析式为
,
所以抛物线的顶点坐标为,.
16.如图,已知在中,,,,,.求:四边形的周长.
【解答】解:,,
四边形是平行四边形,
,,
,
,
,
,
,,即,
四边形的周长.
四、(本大题共2小题,每小题8分,满分16分)
17.如图, 已知是坐标原点,,两点的坐标分别为,.
(1) 以点为位似中心在轴的左侧将放大到两倍, 画出图形;
(2) 分别写出,两点的对应点,的坐标;
(3) 求△的面积 .
【解答】解: (1) 如图;
(2),,
,,
,两点的对应点,的坐标为
,;
(3)
,
.
18.某施工地在道路拓宽施工时,遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为90米的三角形绿化地,由于马路拓宽绿地被占去了一部分,变成了四边形且,原绿化地一边的长由原来的30米缩短成为18米.求被占去的部分面积有多大?它的周长是多少?
【解答】解:由题意可得:,
则,
故,
的长由原来的30米缩短成长18米,
,
即,
解得:,
,
解得:.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,一次函数和反比例函数交于点与点.
(1)求反比例函数和一次函数的解析式;
(2)求的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值的的取值范围.
【解答】(1)解:点与点在反比例函数图象上,
,即反比例函数的解析式为,
当时,,即,
点与点在一次函数图象上,
,解得:
一次函数解析式为;
(2)解:对于,当时,,
;
(3)解:由图象可得,当或时,一次函数的值大于反例函数的值.
20.有一个二次函数满足以下条件:①函数图象与轴的交点坐标分别为,,(点在点的右侧);②对称轴是;③该函数有最小值是.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象中部分的图象向下翻折与原图象未翻折的部分组成图象“”,试结合图象分析:平行于轴的直线与图象“”的交点的个数情况.
【解答】解:(1)由上述信息可知该函数图象的顶点坐标为:,
设二次函数的表达式为:.
该函数图象经过点,
,
解得
二次函数解析式为:.
(2)如图所示:
当时,直线与有一个交点;
当时,直线与有两个交点;
当时,直线与有三个交点;
当时,直线与有两个交点;
当时,直线与有一个交点.
六、(本题满分12分)
21.如图,已知,在锐角中,于点,点在边上,连接交于点,且.
(1)求证:;
(2)联结,求证:.
【解答】证明:(1),
.
,
.
.
,
.
.
.
(2),
.
,
.
.
.
.
,
.
,
.
七、(本题满分12分)
22.我市某乡镇在“精准扶贫”活动中销售一农产品,经分析发现月销售量(万件)与月份(月的关系为:,每件产品的利润(元与月份(月的关系如下表:
1 2 3 4 5 6 7 8 9 10 11 12
19 18 17 16 15 14 13 12 11 10 10 10
(1)请你根据表格求出每件产品利润(元与月份(月的关系式;
(2)若月利润(万元)当月销售量(万件)当月每件产品的利润(元,求月利润(万元)与月份(月的关系式;
(3)当为何值时,月利润有最大值,最大值为多少?
【解答】解;(1)当时,设每件产品利润(元与月份(月的关系式为,
,得,
即当时,每件产品利润(元与月份(月的关系式为,
当时,,
由上可得,;
(2)当时,
,
当时,
,
当时,
,
由上可得,;
(3)当时,,
当时,取得最大值,此时;
当时,,
当时,,
则当时,取得最大值,此时,
由上可得,当为8时,月利润有最大值,最大值144万元.
八、(本题满分14分)
23.我们知道,三角形三个内角平分线的交点叫做三角形的内心,已知点为的内心.
(1)如图1,连接并延长交于点,若,,求的长;
(2)如图2,过点作直线交于点,交于点.
①若,求证:;
②如图3,交于点,若,,求的值.
【解答】解:(1)如图1中,作于.设.
,平分,
,,
在中,,
,,,
,
,,,
在中,,
,
,
.
(2)如图2中,连接、.
是内心,
,
,
,
,
,
,
,
设,,
,
,
,
,
,
,
,
,
.
(3)过点作交的延长线于.
,
,,
,
,
,
.
同课章节目录
