人教版七年级上册数学4.3.3余角和补角的概念与性质 课件(共18张PPT)
文档属性
| 名称 | 人教版七年级上册数学4.3.3余角和补角的概念与性质 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 850.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 16:56:02 | ||
图片预览





文档简介
(共18张PPT)
1
2
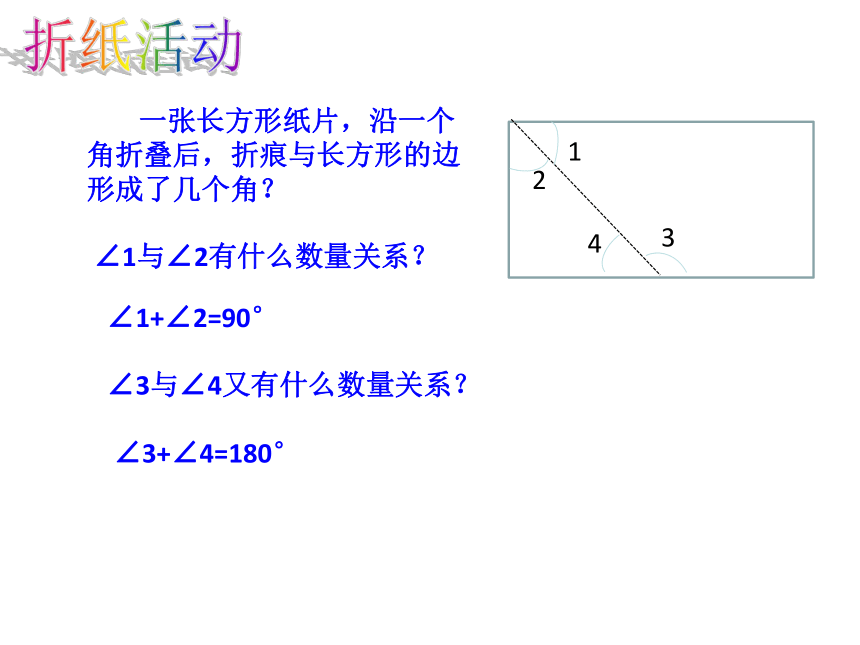
一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了几个角?
3
4
∠1与∠2有什么数量关系?
∠3与∠4又有什么数量关系?
∠1+∠2=90°
∠3+∠4=180°
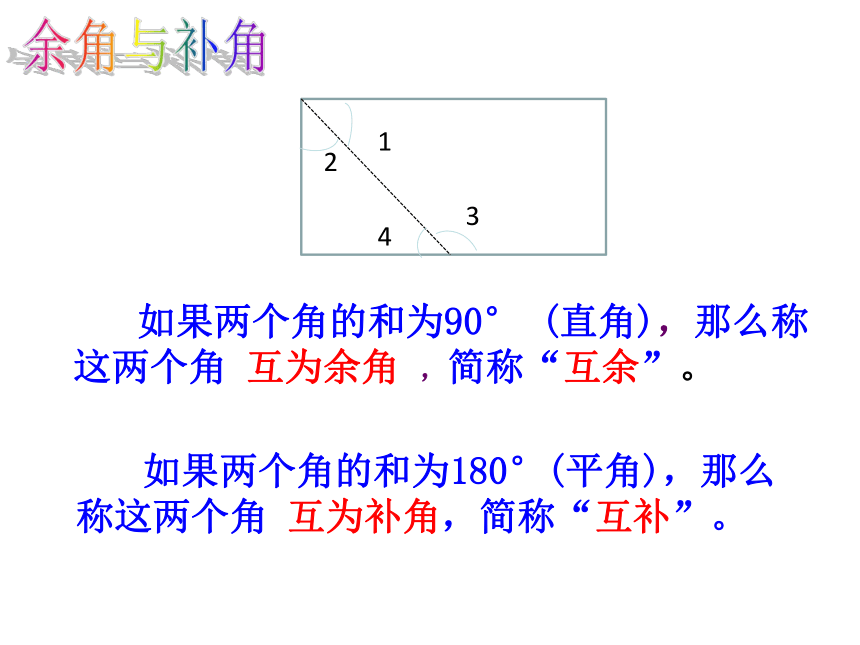
如果两个角的和为90° (直角),那么称这两个角 互为余角 ,简称“互余”。
1
2
3
4
如果两个角的和为180°(平角),那么称这两个角 互为补角,简称“互补”。
(1)定义中的“互为”一词如何理解?
(2)互余、互补的两角是否一定有公共顶点或公共边?
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
提问答疑,理解定义
如果?1与?2互余,那么?1的余角是?2 ,同样?2的余角是?1 ;如果?1与?2互补,那么?1的补角是?2 , 同样?2的补角是?1。
两角互余或互补,只与角的度数有关,与位置无关。
不能,互余或互补是两个角之间的数量关系。
练习:
练习:
2、一个角的补角是它的余角的4倍,求这个
角的余角是多少度?
C
练习:
3
2
你能试画出图中∠1的余角和补角吗?
4
5
同角的补角相等
同角的余角相等
∠2= ∠ 3
∠4= ∠ 5
探究性质
理由:∵∠1与∠2互余 ∴∠1=90o-∠2 ∵∠3与∠1互余 ∴∠3=90o-∠1 ∴∠2=∠3
理由:∵∠1与∠4互补 ∴∠4=180o-∠1 ∵∠1与∠5互补 ∴∠5=90o-∠1 ∴∠4=∠5
等角的余角相等
理由:∵∠1与∠2互余 ∴∠1=90o-∠2 ∵∠3与∠4互余 ∴∠3=90o-∠4 又∵∠2=∠4 ∴∠1=∠3
等角的补角相等
性质:同角或等角的余角相等。
同角或等角的补角相等。
几何语言:
∵ ∠1+ ∠ 2= 900
∠ 1+∠ 3 = 900
∴ ∠ 2 = ∠ 3
(同角的余角相等)
几何语言:
∵ ∠1+ ∠ 2= 900
∠ 3+ ∠ 4 = 900
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
(等角的余角相等)
归纳性质
(2)图中哪几对角是相等的角(直角除外)?
(1)图中有哪几对互余的角?
∠A与∠B互余 ,∠A与∠2互余
∠1与∠B互余 ,∠1与∠2互余
∠B=∠2
∠A=∠1
(同角的余角相等)
(同角的余角相等)
认真观察下面的图形,回答下列问题:
说明它们相等的原因。
性质的应用
1
2
3
4
性质的应用
解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC∠BOC,
所以∠3 +∠2= ∠AOC+ ∠BOC
= (∠AOC+ ∠BOC)
=90°
所以, ∠3 和∠2互为余角,
同理, ∠4 和∠1,∠4 和∠2,∠3 和∠1互为余角.
例3 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?_________.
∠2
,∠4
∠3
,∠1
∠BOD
性质的应用
变式练习
同角或等角的
余角相等
同角或等角的
补角相等
互余 互补
两角间的数量
关系
对应
图形
性质
判断
(5)如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角互为余角. ( )
(3)一个角的补角一定比这个角大。( )
(4)互余的两个角一定都是锐角,两个锐角一定互余. ( )
(2)一个角的补角必为钝角。 ( )
(1)一个角的余角必为锐角。 ( )
×
√
×
×
×
巩固练习
巩固练习
1
2
一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了几个角?
3
4
∠1与∠2有什么数量关系?
∠3与∠4又有什么数量关系?
∠1+∠2=90°
∠3+∠4=180°
如果两个角的和为90° (直角),那么称这两个角 互为余角 ,简称“互余”。
1
2
3
4
如果两个角的和为180°(平角),那么称这两个角 互为补角,简称“互补”。
(1)定义中的“互为”一词如何理解?
(2)互余、互补的两角是否一定有公共顶点或公共边?
(3)∠1 + ∠2 + ∠3 = 90°(180°),能说∠1 、∠2、 ∠3 互余(互补)吗?
提问答疑,理解定义
如果?1与?2互余,那么?1的余角是?2 ,同样?2的余角是?1 ;如果?1与?2互补,那么?1的补角是?2 , 同样?2的补角是?1。
两角互余或互补,只与角的度数有关,与位置无关。
不能,互余或互补是两个角之间的数量关系。
练习:
练习:
2、一个角的补角是它的余角的4倍,求这个
角的余角是多少度?
C
练习:
3
2
你能试画出图中∠1的余角和补角吗?
4
5
同角的补角相等
同角的余角相等
∠2= ∠ 3
∠4= ∠ 5
探究性质
理由:∵∠1与∠2互余 ∴∠1=90o-∠2 ∵∠3与∠1互余 ∴∠3=90o-∠1 ∴∠2=∠3
理由:∵∠1与∠4互补 ∴∠4=180o-∠1 ∵∠1与∠5互补 ∴∠5=90o-∠1 ∴∠4=∠5
等角的余角相等
理由:∵∠1与∠2互余 ∴∠1=90o-∠2 ∵∠3与∠4互余 ∴∠3=90o-∠4 又∵∠2=∠4 ∴∠1=∠3
等角的补角相等
性质:同角或等角的余角相等。
同角或等角的补角相等。
几何语言:
∵ ∠1+ ∠ 2= 900
∠ 1+∠ 3 = 900
∴ ∠ 2 = ∠ 3
(同角的余角相等)
几何语言:
∵ ∠1+ ∠ 2= 900
∠ 3+ ∠ 4 = 900
又∵ ∠ 1 = ∠ 3
∴ ∠ 2 = ∠ 4
(等角的余角相等)
归纳性质
(2)图中哪几对角是相等的角(直角除外)?
(1)图中有哪几对互余的角?
∠A与∠B互余 ,∠A与∠2互余
∠1与∠B互余 ,∠1与∠2互余
∠B=∠2
∠A=∠1
(同角的余角相等)
(同角的余角相等)
认真观察下面的图形,回答下列问题:
说明它们相等的原因。
性质的应用
1
2
3
4
性质的应用
解:因为A,O,B在同一直线上,
所以∠AOC和∠BOC互为补角.
又因为射线OD和射线OE分别平分∠AOC∠BOC,
所以∠3 +∠2= ∠AOC+ ∠BOC
= (∠AOC+ ∠BOC)
=90°
所以, ∠3 和∠2互为余角,
同理, ∠4 和∠1,∠4 和∠2,∠3 和∠1互为余角.
例3 如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角?
如图∠AOC= ∠BOC=∠DOE=90°,则
图中与∠3互余的角是_________,
图中与∠4互余的角是_________,
图中有与∠3互补的角吗?_________.
∠2
,∠4
∠3
,∠1
∠BOD
性质的应用
变式练习
同角或等角的
余角相等
同角或等角的
补角相等
互余 互补
两角间的数量
关系
对应
图形
性质
判断
(5)如果∠1=30°,∠2=25°,∠3=35°,那么∠1、∠2、∠3这三个角互为余角. ( )
(3)一个角的补角一定比这个角大。( )
(4)互余的两个角一定都是锐角,两个锐角一定互余. ( )
(2)一个角的补角必为钝角。 ( )
(1)一个角的余角必为锐角。 ( )
×
√
×
×
×
巩固练习
巩固练习
