3.2.3(整数值)随机数的产生教案
文档属性
| 名称 | 3.2.3(整数值)随机数的产生教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 188.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 10:14:03 | ||
图片预览


文档简介
3.2.3 (整数值)随机数的产生
一、教学目标
1、了解产生随机数的两种方法:
(1)由试验产生随机数;
(2)用计算器或计算机产生随机数
2、会用模拟方法估计概率.
二、课时安排
1课时
三、教学重点
模拟方法估计概率.
四、教学难点
设计和运用模拟方法近似计算概率.
五、教学过程
(一)情景导入
历史上一些掷硬币的试验结果:
这样不断地重复试验花费的时间太多,有没有其他方法可以代替试验呢?
我们可以用随机模拟试验,代替大量复杂的重复动手试验,以便求得随机事件的频率、概率.
(二)讲授新课
1.由试验(如摸球或抽签)产生随机数
例:产生1—25之间的随机整数.
①将25个大小形状相同的小球分别标1,2, …, 24, 25,放入一个袋中,充分搅拌
②从中摸出一个球,这个球上的数就是随机数
2.由计算器或计算机产生随机数
计算器或计算机产生的随机数是根据确定的算法产生的,具有周期性(周期很长),具有类似随机数的性质,但并不是真正的随机数,故叫伪随机数
由计算器或计算机模拟试验的方法为 随机模拟方法或蒙特卡罗方法
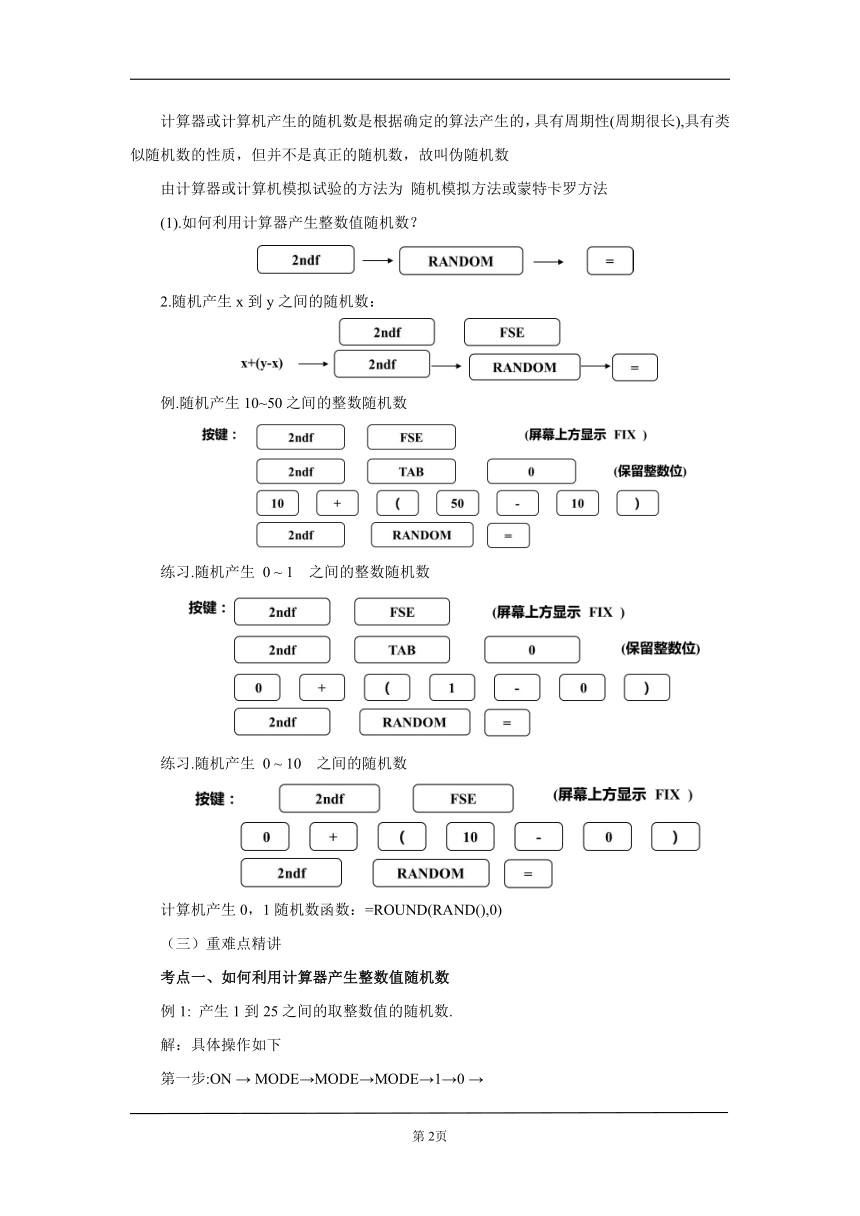
(1).如何利用计算器产生整数值随机数?
2.随机产生x到y之间的随机数:
例.随机产生10~50之间的整数随机数
练习.随机产生 0 ~ 1 之间的整数随机数
练习.随机产生 0 ~ 10 之间的随机数
计算机产生0,1随机数函数:=ROUND(RAND(),0)
(三)重难点精讲
考点一、如何利用计算器产生整数值随机数
例1: 产生1到25之间的取整数值的随机数.
解:具体操作如下
第一步:ON → MODE→MODE→MODE→1→0 →
第二步:25 →SHIFT→RAN#→+ → 0.5 → =
第三步:以后每次按“=”都会产生一个1到25的取整数值的随机数.
若要产生[M,N]的随机整数,操作如下:
第一步:ON → MODE→MODE→MODE→1→0 →
第二步:N-M+1→SHIFT→RAN#→+ → M-0.5 → =
第三步:以后每次按“=”都会产生一个M到N的取整数值的随机数.
温馨提示:
(1)第一步,第二步的操作顺序可以互换;
(2)如果已进行了一次随机整数的产生,再做类似的操作,第一步可省略;
(3)将计算器的数位复原:MODE → MODE → MODE → 3 → 1
练一练
练习:设计用计算器模拟掷硬币的实验20次,统计出现正面的频数和频率
解:(1)规定0表示反面朝上,1表示正面朝上
(2)用计算器产生随机数0,1,操作过程如下:
MODE→MODE→MODE→1→0 → SHIFT → RAN#=
(3)以后每次按“=”直到产生20随机数,并统计出1的个数n
(4)频率f=n/20
用这个频率估计出来的概率精确度如何?误差大吗?
考点二、如何利用计算机产生整数值随机数
用Excel演示: (掷100次硬币正面朝上的频率)
(1)选定A1格,键人“=RANDBETWEEN(0,1)”,按Enter键,则在此格中的数是随机产生的0或1;
(2)选定A1格,点击复制,然后选定要产生随机数的格,比如A2至A100,点击粘贴,则在A2至A100的数均为随机产生的0或1,这样我们就很快就得到了100个随机产生的0或1 ,相当于做了100次随机试验.
(3)选定C1格,键入频数函数“=FREQUENCY(A1:A100,0.5)”,按Enter键,则此格中是数是统计A1至A100中,比0.5小的数的个数,即0出现的频数,也就是反面朝上的频数。
(4)选定D1格,键入“=1-C1/100”,按Enter键,在此格中是数是这100次试验中出现1的频率,即正面朝上的频率。
同时还可以画频率折线图,它更直观地告诉我们:频率在概率附近波动.
例2 .天气预报说,在今后的三天中,每一天下雨的概率均为40%,这三天中恰有两天下雨的概率是多少?
分析:
(1)设计概率模型
利用计算机(计算器)产生0~9之间的(整数值)随机数
约定用1、2、3、4表示下雨,5、6、7、8、9、0表示不下雨以体现下雨的概率是40%.
模拟三天的下雨情况:连续产生三个随机数为一组,作为三天的模拟结果.
(2)进行模拟试验
例如产生20组随机数
(3)统计试验结果
解:我们通过设计模拟试验的方法来解决问题,利用计算器或计算机可以产生0到9之间去整数值的随机数,我们用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,这样可以体现下雨的概率是40%。因为是3天,所以每三个随机数作为一组。
例如,产生20组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
就相当于作了20次试验。在这组数中,如果恰有两个数在1,2,3,4中,则表示恰有两天下雨,他们分别是191,271,932,612,393,即共有5个数。我们得到三天中恰有两天下雨的概率近似为=25%
小结:随机模拟的方法得到的仅是20次试验中恰有2天下雨的频率或概率的近似值,而不是概率.在学过二项分布后,可以计算得到三天中恰有两天下雨的概率:
练一练
天气预报说,在今后的三天中每一天下雨的概率均为30%,用随机模拟的方法进行试验,由1,2,3表示下雨,由4,5,6,7,8,9,0表示不下雨,利用计算器中的随机函数产生0~9之间随机整数的20组数据如下:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
通过以上数据可知三天都不下雨的概率近似为( )
A.0.05 B.0.35
C.0.4 D.0.7
[正解] 选B.由题意知利用计算器模拟求三天都不下雨的概率,产生的20组随机模拟数据中代表三天都不下雨的随机数,应该由4,5,6,7,8,9,0中的三个组成,这样的随机数有:907,966,458,569,556,488,989,共7组随机数,所以所求概率为=0.35,故选B.
(四)归纳小结
随机数具有广泛的应用,可以帮助我们安排和模拟一些试验,这样可以代替我们自己做大量重复试验。通过本节课的学习,我们要熟练掌握随机数产生的方法以及随机模拟试验的步骤:
(1)设计概率模型
(2)进行模拟试验
(3)统计试验结果
(五)随堂检测
1.随机函数RANDBETWEEN(1,2010))产生从整数________ 到整数________的取整数值的随机数.
[答案] 1, 2010
2.一个袋中有7个大小、形状相同的小球,6个白球,1个红球,现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取,试设计一个模拟试验计算恰好第三次摸到红球的概率.
[分析] 根据题意可知所求概率的事件不是古典概型,所以要设计模拟试验来估计其概率,关键是弄清楚用哪些数字来表示题目中红球或白球,然后利用计算机或计算器产生若干组随机数进行估算.
[解析] 用1,2,3,4,5,6表示白球,7表示红球,利用计算器或计算机产生1到7之间取整数值的随机数,因为要求恰好第三次摸到红球的概率,所以每三个随机数作为一组.例如,产生20组随机数.
就相当于做了20次试验,在这组数中,前两个数字不是7,第三个数字恰好是7,就表示第一次、第二次摸的是白球,第三次恰好是红球,它们分别是567和117共两组,因此恰好第三次摸到红球的概率约为=0.1.
六、板书设计
3.2.3 (整数值)随机数的产生
新知探索 例一: 例二: 学生板演练习
七、作业布置
本课同步练习
八、教学反思
第1页
一、教学目标
1、了解产生随机数的两种方法:
(1)由试验产生随机数;
(2)用计算器或计算机产生随机数
2、会用模拟方法估计概率.
二、课时安排
1课时
三、教学重点
模拟方法估计概率.
四、教学难点
设计和运用模拟方法近似计算概率.
五、教学过程
(一)情景导入
历史上一些掷硬币的试验结果:
这样不断地重复试验花费的时间太多,有没有其他方法可以代替试验呢?
我们可以用随机模拟试验,代替大量复杂的重复动手试验,以便求得随机事件的频率、概率.
(二)讲授新课
1.由试验(如摸球或抽签)产生随机数
例:产生1—25之间的随机整数.
①将25个大小形状相同的小球分别标1,2, …, 24, 25,放入一个袋中,充分搅拌
②从中摸出一个球,这个球上的数就是随机数
2.由计算器或计算机产生随机数
计算器或计算机产生的随机数是根据确定的算法产生的,具有周期性(周期很长),具有类似随机数的性质,但并不是真正的随机数,故叫伪随机数
由计算器或计算机模拟试验的方法为 随机模拟方法或蒙特卡罗方法
(1).如何利用计算器产生整数值随机数?
2.随机产生x到y之间的随机数:
例.随机产生10~50之间的整数随机数
练习.随机产生 0 ~ 1 之间的整数随机数
练习.随机产生 0 ~ 10 之间的随机数
计算机产生0,1随机数函数:=ROUND(RAND(),0)
(三)重难点精讲
考点一、如何利用计算器产生整数值随机数
例1: 产生1到25之间的取整数值的随机数.
解:具体操作如下
第一步:ON → MODE→MODE→MODE→1→0 →
第二步:25 →SHIFT→RAN#→+ → 0.5 → =
第三步:以后每次按“=”都会产生一个1到25的取整数值的随机数.
若要产生[M,N]的随机整数,操作如下:
第一步:ON → MODE→MODE→MODE→1→0 →
第二步:N-M+1→SHIFT→RAN#→+ → M-0.5 → =
第三步:以后每次按“=”都会产生一个M到N的取整数值的随机数.
温馨提示:
(1)第一步,第二步的操作顺序可以互换;
(2)如果已进行了一次随机整数的产生,再做类似的操作,第一步可省略;
(3)将计算器的数位复原:MODE → MODE → MODE → 3 → 1
练一练
练习:设计用计算器模拟掷硬币的实验20次,统计出现正面的频数和频率
解:(1)规定0表示反面朝上,1表示正面朝上
(2)用计算器产生随机数0,1,操作过程如下:
MODE→MODE→MODE→1→0 → SHIFT → RAN#=
(3)以后每次按“=”直到产生20随机数,并统计出1的个数n
(4)频率f=n/20
用这个频率估计出来的概率精确度如何?误差大吗?
考点二、如何利用计算机产生整数值随机数
用Excel演示: (掷100次硬币正面朝上的频率)
(1)选定A1格,键人“=RANDBETWEEN(0,1)”,按Enter键,则在此格中的数是随机产生的0或1;
(2)选定A1格,点击复制,然后选定要产生随机数的格,比如A2至A100,点击粘贴,则在A2至A100的数均为随机产生的0或1,这样我们就很快就得到了100个随机产生的0或1 ,相当于做了100次随机试验.
(3)选定C1格,键入频数函数“=FREQUENCY(A1:A100,0.5)”,按Enter键,则此格中是数是统计A1至A100中,比0.5小的数的个数,即0出现的频数,也就是反面朝上的频数。
(4)选定D1格,键入“=1-C1/100”,按Enter键,在此格中是数是这100次试验中出现1的频率,即正面朝上的频率。
同时还可以画频率折线图,它更直观地告诉我们:频率在概率附近波动.
例2 .天气预报说,在今后的三天中,每一天下雨的概率均为40%,这三天中恰有两天下雨的概率是多少?
分析:
(1)设计概率模型
利用计算机(计算器)产生0~9之间的(整数值)随机数
约定用1、2、3、4表示下雨,5、6、7、8、9、0表示不下雨以体现下雨的概率是40%.
模拟三天的下雨情况:连续产生三个随机数为一组,作为三天的模拟结果.
(2)进行模拟试验
例如产生20组随机数
(3)统计试验结果
解:我们通过设计模拟试验的方法来解决问题,利用计算器或计算机可以产生0到9之间去整数值的随机数,我们用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨,这样可以体现下雨的概率是40%。因为是3天,所以每三个随机数作为一组。
例如,产生20组随机数
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
就相当于作了20次试验。在这组数中,如果恰有两个数在1,2,3,4中,则表示恰有两天下雨,他们分别是191,271,932,612,393,即共有5个数。我们得到三天中恰有两天下雨的概率近似为=25%
小结:随机模拟的方法得到的仅是20次试验中恰有2天下雨的频率或概率的近似值,而不是概率.在学过二项分布后,可以计算得到三天中恰有两天下雨的概率:
练一练
天气预报说,在今后的三天中每一天下雨的概率均为30%,用随机模拟的方法进行试验,由1,2,3表示下雨,由4,5,6,7,8,9,0表示不下雨,利用计算器中的随机函数产生0~9之间随机整数的20组数据如下:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
通过以上数据可知三天都不下雨的概率近似为( )
A.0.05 B.0.35
C.0.4 D.0.7
[正解] 选B.由题意知利用计算器模拟求三天都不下雨的概率,产生的20组随机模拟数据中代表三天都不下雨的随机数,应该由4,5,6,7,8,9,0中的三个组成,这样的随机数有:907,966,458,569,556,488,989,共7组随机数,所以所求概率为=0.35,故选B.
(四)归纳小结
随机数具有广泛的应用,可以帮助我们安排和模拟一些试验,这样可以代替我们自己做大量重复试验。通过本节课的学习,我们要熟练掌握随机数产生的方法以及随机模拟试验的步骤:
(1)设计概率模型
(2)进行模拟试验
(3)统计试验结果
(五)随堂检测
1.随机函数RANDBETWEEN(1,2010))产生从整数________ 到整数________的取整数值的随机数.
[答案] 1, 2010
2.一个袋中有7个大小、形状相同的小球,6个白球,1个红球,现任取1个,若为红球就停止,若为白球就放回,搅拌均匀后再接着取,试设计一个模拟试验计算恰好第三次摸到红球的概率.
[分析] 根据题意可知所求概率的事件不是古典概型,所以要设计模拟试验来估计其概率,关键是弄清楚用哪些数字来表示题目中红球或白球,然后利用计算机或计算器产生若干组随机数进行估算.
[解析] 用1,2,3,4,5,6表示白球,7表示红球,利用计算器或计算机产生1到7之间取整数值的随机数,因为要求恰好第三次摸到红球的概率,所以每三个随机数作为一组.例如,产生20组随机数.
就相当于做了20次试验,在这组数中,前两个数字不是7,第三个数字恰好是7,就表示第一次、第二次摸的是白球,第三次恰好是红球,它们分别是567和117共两组,因此恰好第三次摸到红球的概率约为=0.1.
六、板书设计
3.2.3 (整数值)随机数的产生
新知探索 例一: 例二: 学生板演练习
七、作业布置
本课同步练习
八、教学反思
第1页
