2019-2020学年沪教版八年级(上)数学期末考试模拟试卷(解析版)
文档属性
| 名称 | 2019-2020学年沪教版八年级(上)数学期末考试模拟试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-23 17:25:34 | ||
图片预览




文档简介
2019-2020学年沪教版八年级(上)数学期末考试模拟试卷
一.选择题(共6小题,满分18分,每小题3分)
1.在根式,,,中,最简二次根式的个数
A.1个 B.2个 C.3个 D.4个
2.下列方程中是一元二次方程的是
A. B. C. D.
3.已知反比例函数的图象上有三个点,、,、,,若,则下列关系是正确的是
A. B. C. D.
4.用配方法解方程,下列变形正确的是
A. B. C. D.
5.观察下列几个命题:①相等的角是对顶角;②同位角都相等;③三个角相等的三角形是等边三角形;④两直线平行,内错角相等;⑤若,则.其中真命题的个数有
A.0个 B.1个 C.2个 D.3个
6.如图,把一张长方形的纸片沿着折叠,点、分别落在、的位置,且.则
A. B. C. D.
二.填空题(共12小题,满分24分,每小题2分)
7.函数的自变量取值范围是 .
8.不等式的解是 .
9.在实数范围内因式分解: .
10.一元二次方程的根是 .
11.如图,在矩形中,,,点是对角线上的一个动点,连接,以为斜边作的直角三角形,使点和点位于两侧,点从点到点的运动过程中,点的运动路径长是 .
12.元旦晚会,全班同学互赠贺卡,若每两个同学都相互赠送一张贺卡,小明统计全班共送了1640张贺卡,那么全班有多少人?设全班有人,则根据题意可以列出方程 .
13.已知反比例函数的图象在第二、四象限,则的取值范围是 .
14.已知点是直线上的点,且到轴的距离等于3,则点的坐标为 .
15.若关于的方程有实数根, 则的取值范围是 .
16.已知一直角三角形的两直角边长分别为6和8,则斜边上中线的长度是 .
17.如图,在中,,平分交于点,若,点到边的距离为3,则的长是 .
18.如图,三角形纸片中,,,.沿过点的直线折叠这个三角形,使点落在边上的点处,折痕为,则的周长是 .
三.解答题(共4小题,满分24分,每小题6分)
19.计算:
(1)
(2)
20.解下列方程
(1)
(2)
21.甲、乙两车从地开往地,甲车比乙车早出发2小时,并且在途中休息了0.5小时,休息前后速度相同,如图是甲、乙两车行驶的距离与时间的函数图象.解答下列问题:
(1)图中的值为 ;
(2)当时,求甲车行驶路程与时间的函数关系式;
(3)当甲车行驶多长时间后,两车恰好相距?
22.已知:,并且与成正比例,与成反比例.当时,;当时,.
(1)求关于的函数解析式;
(2)求当时的函数值.
四.解答题(共4小题,满分34分)
23.已知:如图,是的高,的垂直平分线分别交,于点,.
(1)求证:;
(2)若添加条件:.求证:.
24.已知,如图,,,分别是,的中点.
求证:①;②.
25.如图,是反比例函数在第一象限图象上一点,连接,过作轴,截取在右侧),连接,交反比例函数的图象于点.
(1)求反比例函数的表达式;
(2)求点的坐标及所在直线解析式;
(3)求的面积.
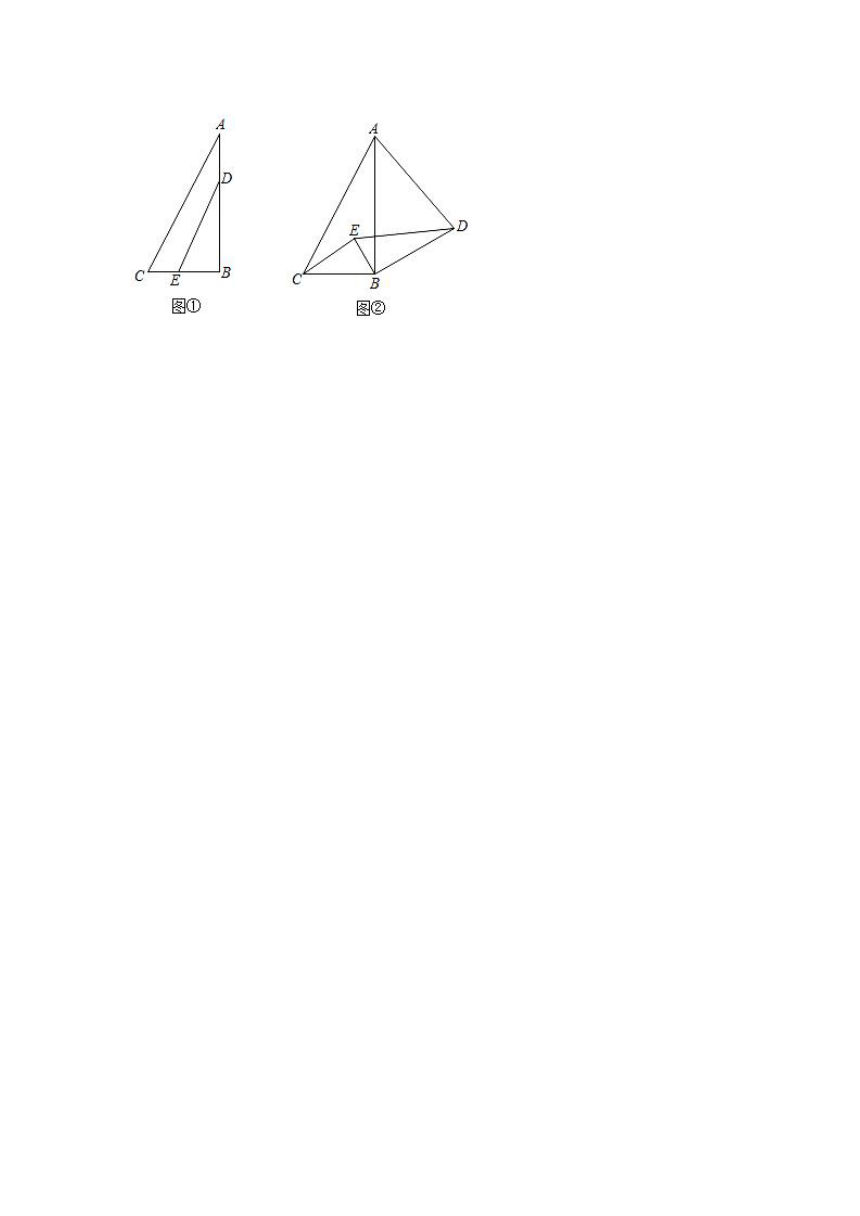
26.如图①,和重叠放置在一起,,且,.
(1)观察猜想:
图①中线段与的数量关系是 ,位置关系是 ;
(2)探究证明:
把绕点顺时针旋转到图②的位置,连接,,判断线段与的数量关系和位置关系如何,并说明理由;
(3)拓展延伸:
若,,当旋转角时,请直接写出线段的长度.
2019-2020学年沪教版八年级(上)数学期末考试模拟试卷
参考答案与试题解析
一.选择题(共6小题,满分18分,每小题3分)
1.在根式,,,中,最简二次根式的个数
A.1个 B.2个 C.3个 D.4个
【解答】解:,,都不是最简二次根式,
,是最简二次根式,
故选:.
2.下列方程中是一元二次方程的是
A. B. C. D.
【解答】解:.分母中含有未知数,不符合一元二次方程的定义,项错误,
.整理得:,属于一元一次方程,不符合一元二次方程的定义,项错误,
.含有两个未知数,不符合一元二次方程的定义,项错误,
.符合一元二次方程的定义,项正确,
故选:.
3.已知反比例函数的图象上有三个点,、,、,,若,则下列关系是正确的是
A. B. C. D.
【解答】解:反比例函数,
函数图象在第二、四象限,且在每个象限内,随的增大而增大,
函数的图象上有三个点,,,、,,且,
,
故选:.
4.用配方法解方程,下列变形正确的是
A. B. C. D.
【解答】解:,
,
则,即,
故选:.
5.观察下列几个命题:①相等的角是对顶角;②同位角都相等;③三个角相等的三角形是等边三角形;④两直线平行,内错角相等;⑤若,则.其中真命题的个数有
A.0个 B.1个 C.2个 D.3个
【解答】解:①相等的角不一定是对顶角,①是假命题;
②只有在两线平行时,同位角相等,②是假命题;
③三个角相等的三角形是等边三角形,③是真命题;
④两直线平行,内错角相等,④是真命题;
⑤若,则,⑤是假命题.
故选:.
6.如图,把一张长方形的纸片沿着折叠,点、分别落在、的位置,且.则
A. B. C. D.
【解答】解:由折叠的性质可得:,
,
设,则,
,
,
解得:,
.
故选:.
二.填空题(共12小题,满分24分,每小题2分)
7.函数的自变量取值范围是 .
【解答】解:根据题意得:,
解得:.
故答案为:.
8.不等式的解是 .
【解答】解:
,
,
故答案为:.
9.在实数范围内因式分解: .
【解答】解:设,
解得:或,
,
故答案为:.
10.一元二次方程的根是 , .
【解答】解:,
,
,,
,,
故答案为:,.
11.如图,在矩形中,,,点是对角线上的一个动点,连接,以为斜边作的直角三角形,使点和点位于两侧,点从点到点的运动过程中,点的运动路径长是 .
【解答】解:的运动路径是的长;
,,
,
当与点重合时,
在中,,,,
,,
当与重合时,,
,,
在中,;
故答案为.
12.元旦晚会,全班同学互赠贺卡,若每两个同学都相互赠送一张贺卡,小明统计全班共送了1640张贺卡,那么全班有多少人?设全班有人,则根据题意可以列出方程 .
【解答】解:设全班有人.根据题意,得
,
故答案是:.
13.已知反比例函数的图象在第二、四象限,则的取值范围是 .
【解答】解:反比例函数的图象在第二、四象限,
,
解得,
故答案为.
14.已知点是直线上的点,且到轴的距离等于3,则点的坐标为 或 .
【解答】解:点是直线上的点,且到轴的距离等于3,
点的横坐标为2,纵坐标为,
点的坐标为或.
故答案为:或.
15.若关于的方程有实数根, 则的取值范围是 .
【解答】解: 当时,
原方程可整理得:, (符 合题意) ,
当时,
关于的方程有实数根,
△,
解得:,
综上可知:的取值范围为:,
故答案为:.
16.已知一直角三角形的两直角边长分别为6和8,则斜边上中线的长度是 5 .
【解答】解:在直角三角形中,两直角边长分别为6和8,
则斜边长,
斜边中线长为,
故答案为 5.
17.如图,在中,,平分交于点,若,点到边的距离为3,则的长是 9 .
【解答】解:如图,过作于,
点到边的距离为3,
,
,平分,,
,
,
,
,
故答案为:9.
18.如图,三角形纸片中,,,.沿过点的直线折叠这个三角形,使点落在边上的点处,折痕为,则的周长是 11 .
【解答】解:由折叠的性质可知,,,
,
,
的周长,
即的周长为.
故答案为:11.
三.解答题(共4小题,满分24分,每小题6分)
19.计算:
(1)
(2)
【解答】解:(1)原式
;
(2)原式
.
20.解下列方程
(1)
(2)
【解答】解:(1),,,
△,
则,
即,;
(2)将方程整理成一般式得,
,,,
△,
则,
即,.
21.甲、乙两车从地开往地,甲车比乙车早出发2小时,并且在途中休息了0.5小时,休息前后速度相同,如图是甲、乙两车行驶的距离与时间的函数图象.解答下列问题:
(1)图中的值为 40 ;
(2)当时,求甲车行驶路程与时间的函数关系式;
(3)当甲车行驶多长时间后,两车恰好相距?
【解答】解:(1)从图上看,甲用小时走了,则1小时走,
故答案为:40;
(2)当时,设与之间的函数关系式为,其中,
将,代入上式得:,解得 ,
.
(3)乙车1.5小时走120米,故其速度为80,
则设乙车行驶的过程与时间之间的解析式为,
将代入上式并解得:,
.
当时,解得.
当时,解得.
甲车行驶1小时(或小时)或小时或小时,两车恰好相距40 .
22.已知:,并且与成正比例,与成反比例.当时,;当时,.
(1)求关于的函数解析式;
(2)求当时的函数值.
【解答】解:(1)由题意可设,,,
.
把,;,代入可得:,
解得,
关于的函数解析式为;
(2)当时,.
四.解答题(共4小题,满分34分)
23.已知:如图,是的高,的垂直平分线分别交,于点,.
(1)求证:;
(2)若添加条件:.求证:.
【解答】(1)证明:是的中垂线,
,,
在和中,
,
.,
是的高,
,
,
.
(2)证明:由(1)得:,,
,,
,分别是,的斜边,上的中线,
,.
,
,
.
24.已知,如图,,,分别是,的中点.
求证:①;②.
【解答】(1)证明:如图,连接、,
,是的中点,
,
;
(2)点是的中点,,
.
25.如图,是反比例函数在第一象限图象上一点,连接,过作轴,截取在右侧),连接,交反比例函数的图象于点.
(1)求反比例函数的表达式;
(2)求点的坐标及所在直线解析式;
(3)求的面积.
【解答】解:(1)将点代入,
得:,
则反比例函数解析式为;
(2)如图,过点作轴于点,
则、,
,
轴,且,
点的坐标为;
设所在直线解析式为,
将点代入得,
所在直线解析式为;
(3)联立解析式:
解得:,
可得点坐标为,
过点作轴,延长交于点,连接,
则点坐标为,
,,,
则的面积.
26.如图①,和重叠放置在一起,,且,.
(1)观察猜想:
图①中线段与的数量关系是 ,位置关系是 ;
(2)探究证明:
把绕点顺时针旋转到图②的位置,连接,,判断线段与的数量关系和位置关系如何,并说明理由;
(3)拓展延伸:
若,,当旋转角时,请直接写出线段的长度.
【解答】解:(1),,
,
,
,
,
,
,
,
,
故答案为:,;
(2),,
理由:把绕点顺时针旋转到图②的位置,
,
,.
,
,
,,
,
延长交于,
,
,
,
,
,
;
(3)如图③,
过作于,
由(2)知,,
,,
,,
,,
,
,,
,
,
,
,,
,
.
同课章节目录
