人教版七年级上册数学4.3.3余角、补角的概念与性质课件(共21张PPT)
文档属性
| 名称 | 人教版七年级上册数学4.3.3余角、补角的概念与性质课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 431.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 07:27:21 | ||
图片预览

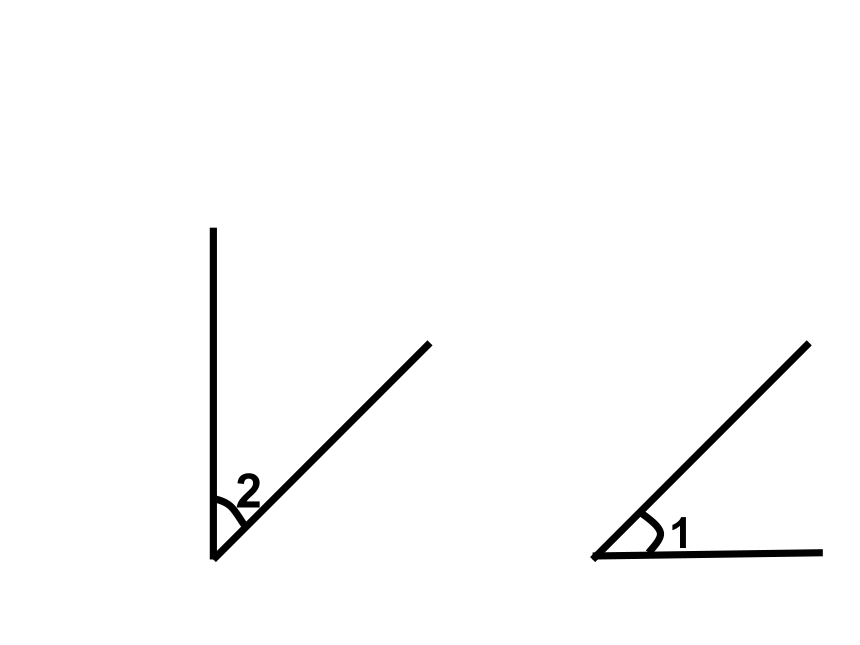




文档简介
(共21张PPT)
余角和补角
2
1
1
2
互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
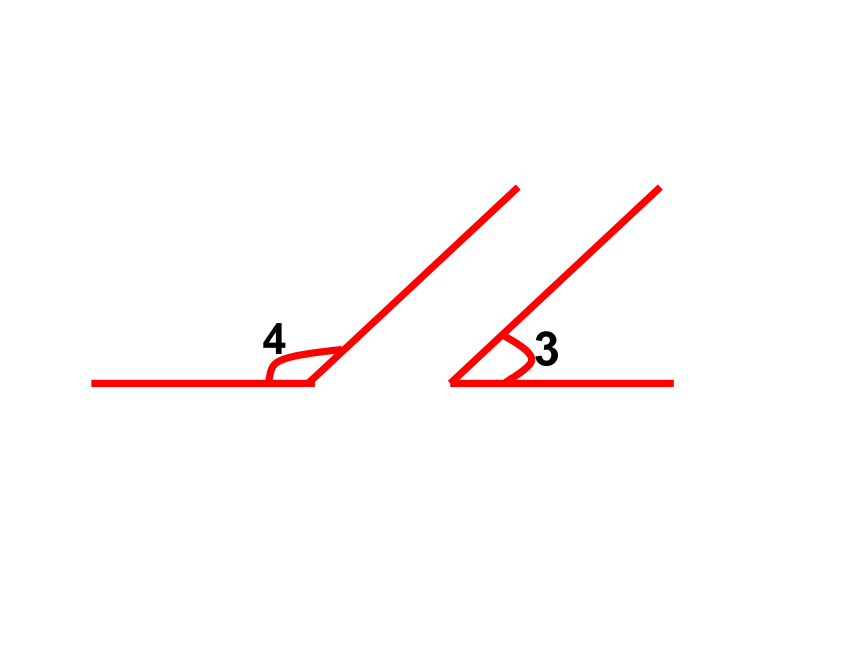
3
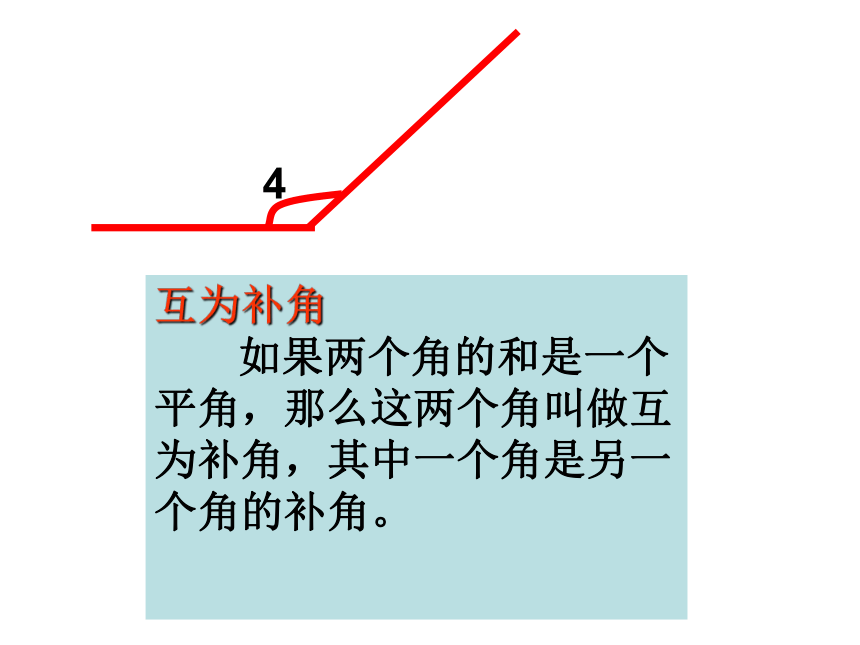
4
3
4
互为补角
如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另一个角的补角。
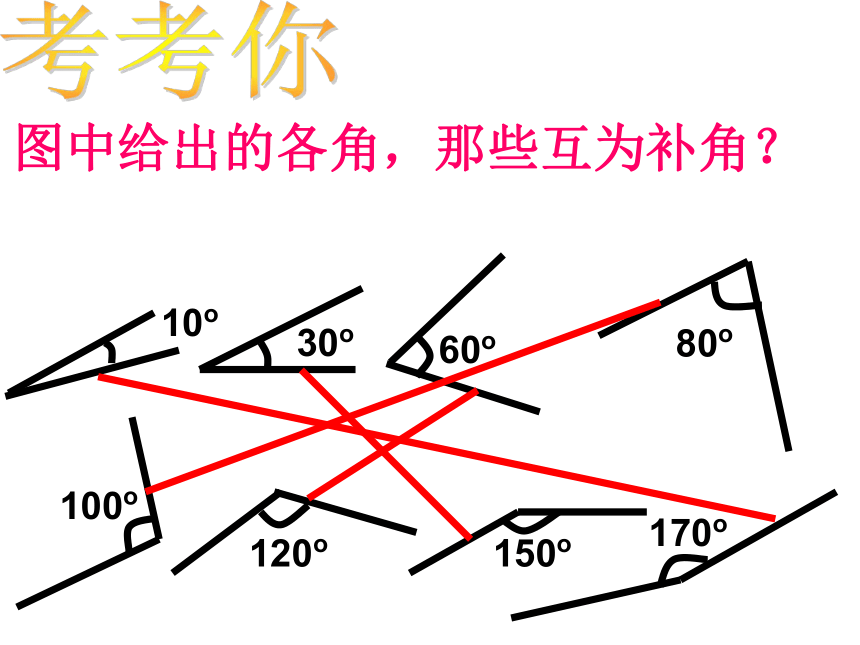
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
我来试一试:
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
x
练习
一、填空
1、70°的余角是 ,补角是 。
2、 ∠ ? ( ∠ ? <90 ° )的余角是 ,它的补角是 。
110 °
20°
90°- ∠ ?
180°- ∠ ?
重要提醒:(如何表示一个角的余角和补角)
锐角∠?的余角是(90 °—∠ ? )
∠?的补角是(180 °—∠ ? )
例1 若一个角的补角等于它的余角的
4 倍,求这个角的度数。
解: 设这个角是x °,则它的补角是 ( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180-x)= 4 (90-x)
解得: x =60
答:这个角的度数是60 °。
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究:余角和补角的性质
例2 如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
解:∠2与∠4相等。
因为∠1与∠2互补;∠3与∠4互补,
所以∠2=180°-∠1;∠4=180°-∠3,
又因为∠1=∠3,
所以∠2=∠4。
补角性质:
等角的补角相等
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
探究:余角和补角的性质
余角性质:
等角的余角相等
∠1+∠2=90°
∠1+∠2=180°
等角的余角相等
等角的补角相等.
互 余 互 补
数量
关系
对
应
图
形
性
质
同角或等角的补角相等
同角或等角的余角相等.
若∠1 + ∠2 =180 °,
则 .( )
若∠1和∠2互补,
则 .( )
若∠3 + ∠4 =90 °,则 .( )
若∠3和∠4互余,
则 .( )
3
1
2
∠1和∠2互补
互补定义
∠1 + ∠2 =180 °
互补定义
∠3和∠4互余
互余定义
∠3 + ∠4 =90 °
互余定义
补角性质:
同角或等角的补角相等。
余角性质:
同角或等角的余角相等。
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2
A
O
B
C
D
(同角的余角相等)
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等。
同角或等角的补角相等。
互为余角 互为补角
对应图形
数量关系
性 质
余角和补角
2
1
1
2
互为余角
如果两个角的和是一个直角,那么这两个角叫做互为余角,其中一个角是另一个角的余角。
图中给出的各角,那些互为余角?
10o
30o
60o
80o
50o
40o
3
4
3
4
互为补角
如果两个角的和是一个平角,那么这两个角叫做互为补角,其中一个角是另一个角的补角。
图中给出的各角,那些互为补角?
10o
30o
60o
80o
100o
120o
150o
170o
我来试一试:
27°37′
117°37′
85°
175°
58°
148°
45°
135°
103°
13°
∠α ∠α的余角 ∠α的补角
5°
32°
45°
77°
62°23′
x
练习
一、填空
1、70°的余角是 ,补角是 。
2、 ∠ ? ( ∠ ? <90 ° )的余角是 ,它的补角是 。
110 °
20°
90°- ∠ ?
180°- ∠ ?
重要提醒:(如何表示一个角的余角和补角)
锐角∠?的余角是(90 °—∠ ? )
∠?的补角是(180 °—∠ ? )
例1 若一个角的补角等于它的余角的
4 倍,求这个角的度数。
解: 设这个角是x °,则它的补角是 ( 180°-x°),余角是(90°-x°) 。
根据题意得:
(180-x)= 4 (90-x)
解得: x =60
答:这个角的度数是60 °。
如图∠1 与∠2互补,∠3 与∠4互补 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
2
1
4
3
探究:余角和补角的性质
例2 如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
解:∠2与∠4相等。
因为∠1与∠2互补;∠3与∠4互补,
所以∠2=180°-∠1;∠4=180°-∠3,
又因为∠1=∠3,
所以∠2=∠4。
补角性质:
等角的补角相等
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
4
3
探究:余角和补角的性质
余角性质:
等角的余角相等
∠1+∠2=90°
∠1+∠2=180°
等角的余角相等
等角的补角相等.
互 余 互 补
数量
关系
对
应
图
形
性
质
同角或等角的补角相等
同角或等角的余角相等.
若∠1 + ∠2 =180 °,
则 .( )
若∠1和∠2互补,
则 .( )
若∠3 + ∠4 =90 °,则 .( )
若∠3和∠4互余,
则 .( )
3
1
2
∠1和∠2互补
互补定义
∠1 + ∠2 =180 °
互补定义
∠3和∠4互余
互余定义
∠3 + ∠4 =90 °
互余定义
补角性质:
同角或等角的补角相等。
余角性质:
同角或等角的余角相等。
如图∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
答: ∠1 = ∠2
因为∠1+ ∠BOD = 90 °
∠2+ ∠BOD = 90 °
所以∠1 = ∠2
A
O
B
C
D
(同角的余角相等)
1
2
∠1+ ∠2 = 90 °
∠1+ ∠2 = 180 °
同角或等角的余角相等。
同角或等角的补角相等。
互为余角 互为补角
对应图形
数量关系
性 质
