2019-2020学年上海市八年级(上)数学期末考试模拟试卷(含解析)
文档属性
| 名称 | 2019-2020学年上海市八年级(上)数学期末考试模拟试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 871.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-29 21:45:16 | ||
图片预览




文档简介
2019-2020学年上海市八年级(上)数学期末考试模拟试卷
一.选择题(共6小题,满分18分)
1.下列各式中能与是合并的是( )
A. B. C. D.
2.设某矩形的面积为S,相邻的两条边长分别为x和y.那么当S一定时,给出以下四个结论:
①x是y的正比例函数;②y是x的正比例函数;③x是y的反比例函数;④y是x的反比例函数
其中正确的为( )
A.①,② B.②,③ C.③,④ D.①,④
3.若三角形的三边长为下列各组数:①5,12,13;②11,12,15;③9,40,41;④15,20,25,则其中直角三角形有( )个.
A.l B.2 C.3 D.4
4.已知函数中,在每个象限内,y随x的增大而增大,那么它和函数y=kx(k≠0)在同一直角坐标平面内的大致图象是( )
A. B.
C. D.
5.下列说法正确的是( )
A.一个定理的逆命题就是这个定理的逆定理
B.原命题和逆命题同真同假
C.到角的两边距离相等的点的轨迹是这个角的平分线
D.如果CA=CB,则过点C垂直AB的直线必平分线段AB
6.已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
A. B. C. D.
二.填空题(共12小题,满分36分,每小题3分)
7.若a,b都是实数,b=+﹣2,则ab的值为 .
8.计算:= ;|﹣|= .
9.已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a= .
10.关于x的一元二次方程x2﹣2x+m=0有两个实数根,则m的取值范围是 .
11.在实数范围内因式分解:9x2﹣5= .
12.正比例函数中,y随着x的增大而 .
13.反比例函数的图象在第一、三象限,则m的取值范围是 .
14.用20cm长的绳子围成一个等腰三角形,设它的底边长ycm,腰长为xcm,则y与x之间的函数关系式为 (写出自变量x的取值范围).
15.把命题“等角的补角相等”改写成“如果…那么…”的形式是 .
16.如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是 度.
17.如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有 对全等三角形.
18.一道作图题如下:
已知:如图1,∠ABC,及BC边上一点D.求作:一点P,使点P到∠ABC两边的距离相等,且到B,D两点的距离相等.
下面是一位同学的作图过程(图2):
(1)作∠ABC的平分线BE;
(2)作线段BD的垂直平分线l,与BE交于点P.
所以点P就是所求作的点.则该作图的依据是 .
三.解答题(共3小题,满分24分,每小题8分)
19.计算:﹣4﹣2(﹣1).
20.(2y+1)2+3(2y+1)+2=0.
21.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣x+3交AB,BC分别于点M,N,反比例函数y=的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
四.解答题(共4小题,满分42分)
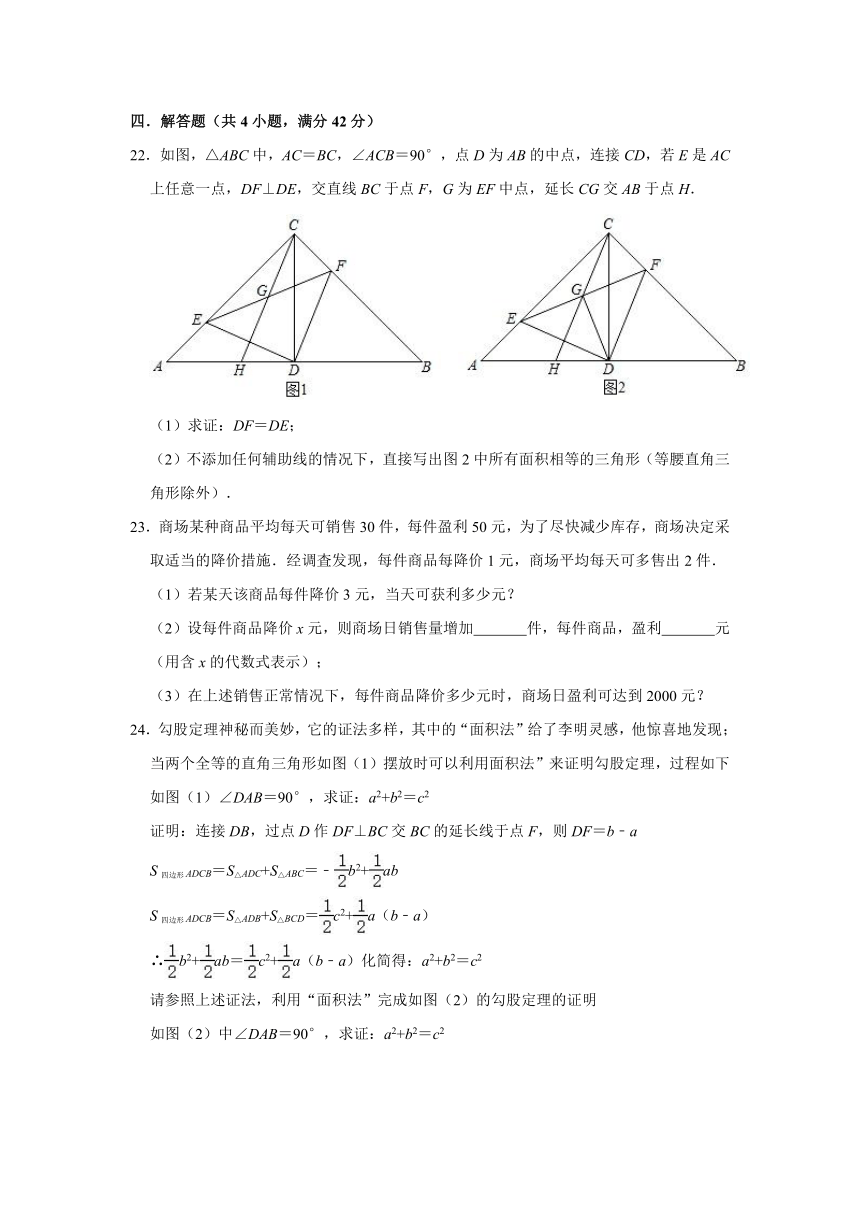
22.如图,△ABC中,AC=BC,∠ACB=90°,点D为AB的中点,连接CD,若E是AC上任意一点,DF⊥DE,交直线BC于点F,G为EF中点,延长CG交AB于点H.
(1)求证:DF=DE;
(2)不添加任何辅助线的情况下,直接写出图2中所有面积相等的三角形(等腰直角三角形除外).
23.商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若某天该商品每件降价3元,当天可获利多少元?
(2)设每件商品降价x元,则商场日销售量增加 件,每件商品,盈利 元(用含x的代数式表示);
(3)在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?
24.勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b﹣a
S四边形ADCB=S△ADC+S△ABC=﹣b2+ab
S四边形ADCB=S△ADB+S△BCD=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明
如图(2)中∠DAB=90°,求证:a2+b2=c2
25.数学课上,老师出示了如下框中的题目.
如图(1),在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试确定线段AE与DB的大小关系,并说明理由.
小敏与同桌小聪谈论后,进行了如下回答:
(1)特殊入手,探索结论 如图(1),当点E为AB的中点时.确定线段AE与DB的大小关系.直接写出结论:AE DB(填“>“,“<“或“=“)
(2)特例启发,如图(2),解答题目判断AE与DB的大小关系,并证明
(3)拓展结论,设计新题 在等边三角形ABC中,点E在射线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长.
2019-2020学年上海市八年级(上)数学期末考试模拟试卷
参考答案与试题解析
一.选择题(共6小题,满分12分)
1.下列各式中能与是合并的是( )
A. B. C. D.
【解答】解:,,,=,
∴能和合并的是.
故选:A.
2.设某矩形的面积为S,相邻的两条边长分别为x和y.那么当S一定时,给出以下四个结论:
①x是y的正比例函数;②y是x的正比例函数;③x是y的反比例函数;④y是x的反比例函数
其中正确的为( )
A.①,② B.②,③ C.③,④ D.①,④
【解答】解:设某矩形的面积为S,相邻的两条边长分别为x和y.
那么当S一定时,x与y的函数关系式是y=,
由于S≠0,且是常数,因而这个函数是一y是x的反比例函数.
同理x是y的反比例函数.
正确的是:③,④.
故选:C.
3.若三角形的三边长为下列各组数:①5,12,13;②11,12,15;③9,40,41;④15,20,25,则其中直角三角形有( )个.
A.l B.2 C.3 D.4
【解答】解:①、∵52+122=169=132,∴能组成直角三角形,故本选项正确;
②、∵112+122=265≠152=225,∴不能组成直角三角形,故本选项错误;
③、92+402=1681=412,∴能组成直角三角形,故本选项正确;
④、152+202=625=252,∴能组成直角三角形,故本选项正确.
故选:C.
4.已知函数中,在每个象限内,y随x的增大而增大,那么它和函数y=kx(k≠0)在同一直角坐标平面内的大致图象是( )
A. B.
C. D.
【解答】解:∵函数中,在每个象限内,y随x的增大而增大,
∴k<0,
∴双曲线在第二、四象限,
∴函数y=kx的图象经过第二、四象限,
故选:B.
5.下列说法正确的是( )
A.一个定理的逆命题就是这个定理的逆定理
B.原命题和逆命题同真同假
C.到角的两边距离相等的点的轨迹是这个角的平分线
D.如果CA=CB,则过点C垂直AB的直线必平分线段AB
【解答】解:A、一个定理的逆命题一定存在,但这个定理可能不存在,故本选项错误;
B、原命题和逆命题的真与假没关系,故本选项错误;
C、根据角平分线性质的逆定理,到角两边距离相等的点,在这个角的平分线上,∵角的平分线是射线,故本选项错误;
D、如果CA=CB,则过点C垂直AB的直线必平分线段AB,故本选项正确.
故选:D.
6.已知:如图,点P是正方形ABCD的对角线AC上的一个动点(A、C除外),作PE⊥AB于点E,作PF⊥BC于点F,设正方形ABCD的边长为x,矩形PEBF的周长为y,在下列图象中,大致表示y与x之间的函数关系的是( )
A. B. C. D.
【解答】解:由题意可得:△APE和△PCF都是等腰直角三角形.
∴AE=PE,PF=CF,那么矩形PEBF的周长等于2个正方形的边长.则y=2x,为正比例函数.
故选:A.
二.填空题(共12小题,满分36分,每小题3分)
7.若a,b都是实数,b=+﹣2,则ab的值为 4 .
【解答】解:∵b=+﹣2,
∴1﹣2a=0,
解得:a=,
则b=﹣2,
故ab=()﹣2=4.
故答案为:4.
8.计算:= ;|﹣|= 2 .
【解答】解:==,|﹣|==2,
故答案为:,2.
9.已知点A(3a+5,a﹣3)在二、四象限的角平分线上,则a= ﹣ .
【解答】解:∵点A(3a+5,a﹣3)在二、四象限的角平分线上,
∴3a+5+a﹣3=0,
∴a=﹣.
故答案为:﹣.
10.关于x的一元二次方程x2﹣2x+m=0有两个实数根,则m的取值范围是 m≤1 .
【解答】解:由题意知,△=4﹣4m≥0,
∴m≤1,
故答案为:m≤1.
11.在实数范围内因式分解:9x2﹣5= .
【解答】解:9x2﹣5=(3x)2﹣()2,
=.
12.正比例函数中,y随着x的增大而 减小 .
【解答】解:∵正比例函数中,k=﹣<0,
∴y随着x的增大而减小.
故答案为:减小.
13.反比例函数的图象在第一、三象限,则m的取值范围是 m>1 .
【解答】解:∵反比例函数的图象在第一、三象限,
∴m﹣1>0,
解得m>1.
故答案为:m>1.
14.用20cm长的绳子围成一个等腰三角形,设它的底边长ycm,腰长为xcm,则y与x之间的函数关系式为 y=﹣2x+20(5<x<10) (写出自变量x的取值范围).
【解答】解:∵2x+y=20,
∴y=20﹣2x,即x<10,
∵两边之和大于第三边,
∴x>5.
故答案为:y=﹣2x+20(5<x<10).
15.把命题“等角的补角相等”改写成“如果…那么…”的形式是 如果两个角是等角的补角,那么它们相等 .
【解答】解:题设为:两个角是等角的补角,结论为:相等,
故写成“如果…那么…”的形式是:如果两个角是等角的补角,那么它们相等.
故答案为:如果两个角是等角的补角,那么它们相等.
16.如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是 50 度.
【解答】解:∵DM是AB的垂直平分线,
∴AD=BD,
∴∠ABD=∠A,
∵等腰△ABC中,AB=AC,
∴∠ABC=∠C=,
∴∠DBC=∠ABC﹣∠ABD=﹣∠A=15°,
解得:∠A=50°.
故答案为:50.
17.如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有 3 对全等三角形.
【解答】解:OP平分∠MON,PE⊥OM于E,PF⊥ON于F,
∴PE=PF,∠1=∠2,
在△AOP与△BOP中,
,
∴△AOP≌△BOP,
∴AP=BP,
在△EOP与△FOP中,
,
∴△EOP≌△FOP,
在Rt△AEP与Rt△BFP中,
,
∴Rt△AEP≌Rt△BFP,
∴图中有3对全等三角形,
故答案为:3.
18.一道作图题如下:
已知:如图1,∠ABC,及BC边上一点D.求作:一点P,使点P到∠ABC两边的距离相等,且到B,D两点的距离相等.
下面是一位同学的作图过程(图2):
(1)作∠ABC的平分线BE;
(2)作线段BD的垂直平分线l,与BE交于点P.
所以点P就是所求作的点.则该作图的依据是 角平分线上的点到角的两边距离相等或线段的垂直平分线上的点到线段的两个端点的距离相等. .
【解答】解:∵点P在∠ABC的平分线上,
∴点P到∠ABC两边的距离相等(角平分线上的点到角的两边距离相等),
∵点P在线段BD的垂直平分线上,
∴PB=PD(线段的垂直平分线上的点到线段的两个端点的距离相等),
故答案为角平分线上的点到角的两边距离相等或线段的垂直平分线上的点到线段的两个端点的距离相等.
三.解答题(共3小题,满分24分,每小题8分)
19.计算:﹣4﹣2(﹣1).
【解答】解:原式=
=
=2
20.(2y+1)2+3(2y+1)+2=0.
【解答】解:设2y+1=t.则由原方程,得
t2+3t+2=0,
∴(t+1)(t+2)=0,
∴t+1=0或t+2=0,
解得t=﹣1或t=﹣2;
①当t=﹣1时,2y+1=﹣1,解得y=﹣1;
②当t=﹣2时,2y+1=﹣2,解得y=﹣.
综上所述,原方程的解是:y=﹣1或y=﹣.
21.如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣x+3交AB,BC分别于点M,N,反比例函数y=的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
【解答】解:(1)∵B(4,2),四边形OABC是矩形,
∴OA=BC=2,
将y=2代入y=﹣x+3得:x=2,
∴M(2,2),
将x=4代入y=﹣x+3得:y=1,
∴N(4,1),
把M的坐标代入y=得:k=4,
∴反比例函数的解析式是y=;
(2)由题意可得:
S四边形BMON=S矩形OABC﹣S△AOM﹣S△CON
=4×2﹣×2×2﹣×4×1
=4;
∵△OPM的面积与四边形BMON的面积相等,
∴OP×AM=4,
∵AM=2,
∴OP=4,
∴点P的坐标是(0,4)或(0,﹣4).
四.解答题(共4小题,满分42分)
22.如图,△ABC中,AC=BC,∠ACB=90°,点D为AB的中点,连接CD,若E是AC上任意一点,DF⊥DE,交直线BC于点F,G为EF中点,延长CG交AB于点H.
(1)求证:DF=DE;
(2)不添加任何辅助线的情况下,直接写出图2中所有面积相等的三角形(等腰直角三角形除外).
【解答】(1)证明:∵∠ACB=90°,D为AB的中点,AC=BC,
∴CD=AD=BD,
又∵AC=BC,
∴CD⊥AB,
∴∠EDA+∠EDC=90°,∠DCF=∠DAE=45°,
∵DF⊥DE,
∴∠EDF=∠EDC+∠CDF=90°,
∴∠ADE=∠CDF,
在△ADE和△CDF中
,
∴△ADE≌△CDF(ASA),
∴DE=DF.
(2)∵△ADE≌△CDF,
∴S△ADE=S△CDF,
∵S△ADC=S△CDB,
∴S△CDE=S△BDF,
∵∠ACB=90°,G为EF的中点,
∴CG=EG=FG,
∵∠EDF=90°,G为EF的中点,
∴DG=EG=FG,
∴CG=DG,
∴∠GCD=∠CDG,
又∵CD⊥AB,
∴∠CDH=90°,
∴∠GHD+∠GCD=90°,∠HDG+∠GDC=90°,
∴∠GHD=∠HDG,
∴GH=GD,
∴CG=GH.
∴S△GHD=S△CGD.
∵G为EF中点,
∴S△EGC=S△GFC.
则面积相等的三角形(等腰直角三角形除外)有S△GHD=S△CGD,S△ADE=S△CDF,S△CDE=S△BDF,S△EGC=S△GFC.
23.商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施.经调査发现,每件商品每降价1元,商场平均每天可多售出2件.
(1)若某天该商品每件降价3元,当天可获利多少元?
(2)设每件商品降价x元,则商场日销售量增加 2x 件,每件商品,盈利 50﹣x 元(用含x的代数式表示);
(3)在上述销售正常情况下,每件商品降价多少元时,商场日盈利可达到2000元?
【解答】解:(1)当天盈利:(50﹣3)×(30+2×3)=1692(元).
答:若某天该商品每件降价3元,当天可获利1692元.
(2)∵每件商品每降价1元,商场平均每天可多售出2件,
∴设每件商品降价x元,则商场日销售量增加2x件,每件商品,盈利(50﹣x)元.
故答案为:2x;50﹣x.
(3)根据题意,得:(50﹣x)×(30+2x)=2000,
整理,得:x2﹣35x+250=0,
解得:x1=10,x2=25,
∵商城要尽快减少库存,
∴x=25.
答:每件商品降价25元时,商场日盈利可达到2000元.
24.勾股定理神秘而美妙,它的证法多样,其中的“面积法”给了李明灵感,他惊喜地发现;当两个全等的直角三角形如图(1)摆放时可以利用面积法”来证明勾股定理,过程如下
如图(1)∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作DF⊥BC交BC的延长线于点F,则DF=b﹣a
S四边形ADCB=S△ADC+S△ABC=﹣b2+ab
S四边形ADCB=S△ADB+S△BCD=c2+a(b﹣a)
∴b2+ab=c2+a(b﹣a)化简得:a2+b2=c2
请参照上述证法,利用“面积法”完成如图(2)的勾股定理的证明
如图(2)中∠DAB=90°,求证:a2+b2=c2
【解答】证明:连结BD,过点B作DE边上的高BF,则BF=b﹣a,
∵S五边形ACBED=S△ACB+S△ABE+S△ADE=ab+b2+ab,
又∵S五边形ACBED=S△ACB+S△ABD+S△BDE=ab+c2+a(b﹣a),
∴ab+b2+ab=ab+c2+a(b﹣a),
∴a2+b2=c2.
25.数学课上,老师出示了如下框中的题目.
如图(1),在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试确定线段AE与DB的大小关系,并说明理由.
小敏与同桌小聪谈论后,进行了如下回答:
(1)特殊入手,探索结论 如图(1),当点E为AB的中点时.确定线段AE与DB的大小关系.直接写出结论:AE = DB(填“>“,“<“或“=“)
(2)特例启发,如图(2),解答题目判断AE与DB的大小关系,并证明
(3)拓展结论,设计新题 在等边三角形ABC中,点E在射线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长.
【解答】解:(1)如图1,过点E作EF∥BC,交AC于点F,
∵△ABC为等边三角形,
∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
∴∠EDB=∠FEC,
在△BDE和△FEC中,
,
∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD,
故答案为:=;
(2)如图2,过点E作EF∥BC,交AC于点F,
∵△ABC为等边三角形,
∴∠AFE=∠ACB=∠ABC=60°,△AEF为等边三角形,
∴∠EFC=∠EBD=120°,EF=AE,
∵ED=EC,
∴∠EDB=∠ECB,∠ECB=∠FEC,
∴∠EDB=∠FEC,
在△BDE和△FEC中,
,
∴△BDE≌△FEC(AAS),
∴BD=EF,
∴AE=BD,
故答案为:=;
(3)因为AE=2,△ABC的边长为1,所以E点可能在线段BA上,也可能在BA的延长线上,
当点E在AB时,同(2)可知BD=AE=2,则CD=BC+BD=1+2=3,
当点E在BA的延长线上时,如图3,过点E作EF∥BC,交CA的延长线于点F,
则∠F=∠FCB=∠B=60°,
∠FEC+∠ECD=∠FEC+∠EDC=180°,
∴∠EDB=∠FEC,
且ED=EC,
在△BDE和△FEC中,
,
∴△BDE≌△FEC(AAS),
∴EF=BD,
又∵可判定△AEF为等边三角形,
∴BD=EF=AE=2,
∴CD=BC+BD=2+1=3,
综上所述,CD的长度为3.
同课章节目录
