沪教版数学七年级上册期末复习学案(解析版)
文档属性
| 名称 | 沪教版数学七年级上册期末复习学案(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 08:41:22 | ||
图片预览



文档简介
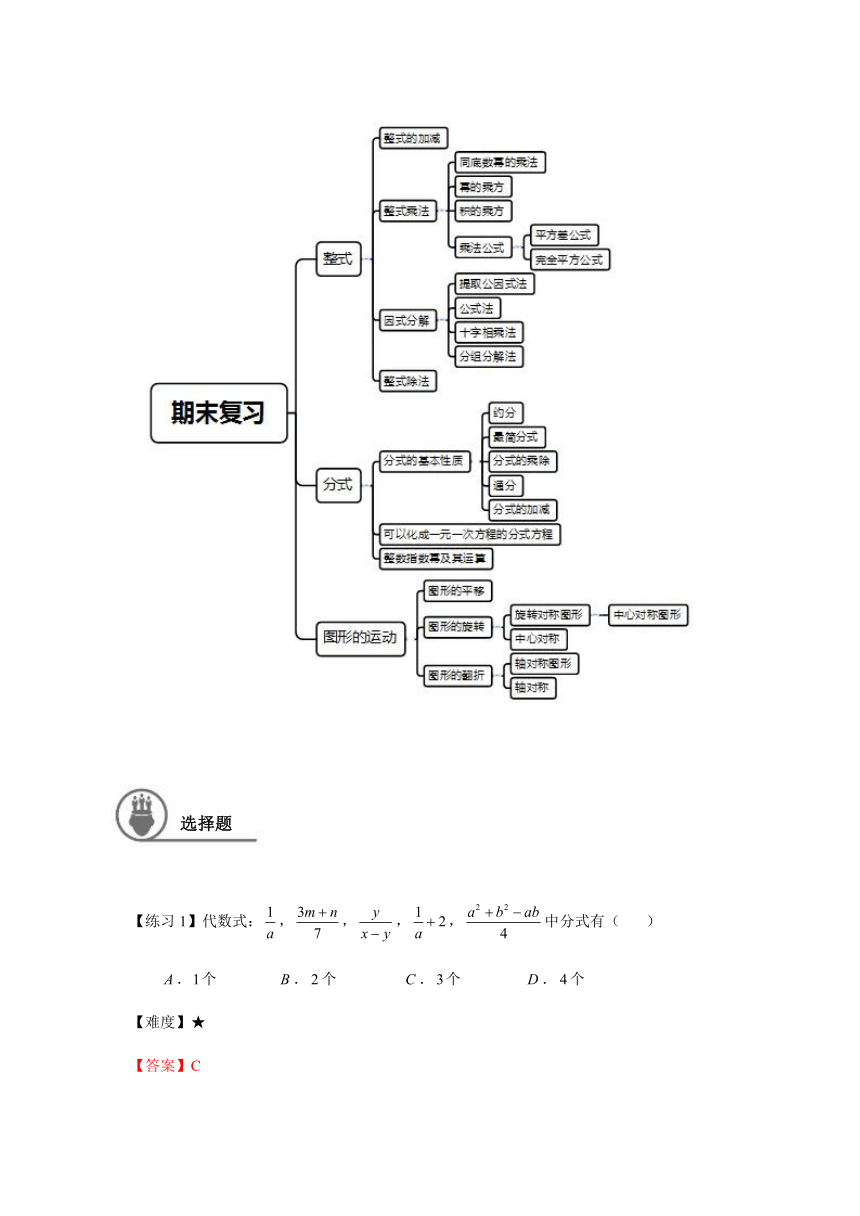
本学期一共学习了三章内容,分别是整式、分式、图形的运动.通过本讲内容,对本学期所学内容进行全面复习.
【练习1】代数式:,,,,中分式有( )
.个 .个 .个 .个
【难度】★
【答案】C
【解析】分式指分子分母均为整式,且分母中必须含有字母.
【总结】本题考查了分式的基本概念.
【练习2】小马虎在下面的计算中只做对了一道题,他做对的题目是 ( )
. .
. .
【难度】★
【答案】D
【解析】A是完全平方公式,;B答案为;C不能运算.
【总结】本题考查了整式的基本运算.
【练习3】分式,,的最简公分母是( )
. . . .
【难度】★
【答案】C
【解析】当分母均为单项式时,取各系数的最小公倍数,相同字母的最高次幂,
所有不同字母都写在公分母里.
【总结】本题考查了最简公分母的概念.
【练习4】在下图右侧的四个三角形中,由既不能经过旋转也不能经过平
移得到的三角形是( )
【难度】★
【答案】B
【解析】由图可以知道A、C、D都可由经过旋转和平移得到,而B选项必须经过翻
折才能和其重合.
【总结】本题主要考查了图形旋转和平移的特征.
【练习5】下列图形中,是中心对称图形的是( )
【难度】★
【答案】D
【解析】如果把一个图形绕某一点旋转后能与自身重合,这个图形就是中心对称图形.
常见的中心对称图形有:线段、矩形、菱形、正方形、平行四边形、圆、边数为偶数的
正多边形等.
【总结】本题主要考查了中心对称图形的定义.
【练习6】从甲到乙的图形变换,判断全正确的是 ( )
.(1)翻折,(2)旋转,(3)平移 .(1)翻折,(2)平移,(3)旋转
.(1)平移,(2)翻折,(3)旋转 .(1)平移,(2)旋转,(3)翻折
【难度】★
【答案】A
【解析】由图可知:(1)把甲翻折即可得到乙;
(2)绕甲的直角顶点顺时针旋转即可得到乙;
(3)把甲先向右平移,再向上平移即可得到乙.
【总结】本题考查了图形变换的三种方式.
【练习7】已知,那么的值为( )
. . . .
【难度】★★
【答案】C
【解析】已知:,则.
【总结】本题考查了同底数幂的运算的综合运用.
【练习8】,则下列不等式错误的是( )
. . . .
【难度】★★
【答案】A
【解析】由知,倒数大的反而小,故A错误.
【总结】本题考查了不等式的性质.
【练习9】一小包柠檬茶冲剂,用克水可冲泡成浓度为的饮料,求这包柠檬茶冲剂多
少克?若设这包柠檬茶冲剂有克,则得到的方程( )
. .
. .
【难度】★★
【答案】B
【解析】由得,.
【总结】本题考查了溶液浓度的公式在列分式方程中的运用.
【练习10】小明出门前从镜子中看到墙上的时钟正好如图所示,他出门不到一小时后回到家
发现该时钟的分钟正好转了180°,那么他出门后到家的时间是 ( )
A、3:00 B、3:30 C、9:30 D、10:00
【难度】★★
【答案】D
【解析】由对称得出门前时间为9:30,再由旋转得10:00.
【总结】本题考查了图形的旋转在实际生活中的运用.
【练习11】因式分解:.
【难度】★
【答案】.
【解析】直接利用公式法中完全平方公式进行分解即可.
【总结】本题考查了因式分解的方法.
【练习12】用科学记数表示.
【难度】★
【答案】.
【解析】绝对值小于1的正数也可以用科学计数法表示,一般形式为.
【总结】本题考查了科学计数法中负整数指数幂的表示.
【练习13】计算:_______________.
【难度】★
【答案】.
【解析】.
【总结】本题考查了平方差公式在整式乘法中的应用.
【练习14】计算:_______________.
【难度】★
【答案】.
【解析】多项式除以单项式用多项式的每一项除以单项式,再把结果相加.
【总结】本题考查了多项式除以单项式的运算.
【练习15】①等边三角形 ;②平行四边形;③长方形 ;④菱形; ⑤等腰直角三角形;
⑥正五边形,其中不是轴对称图形的是_______________(填序号)
【难度】★
【答案】②
【解析】在平面内,如果一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这样的 图形叫轴对称图形.显然①③④⑤⑥都可以.
【总结】本题考查了轴对称图形的定义.
【练习16】五角星是一个旋转对称图形,它至少旋转_______度后,能与自身重合.
【难度】★
【答案】.
【解析】根据旋转对称图形的概念可知:该图形被平分成五部分,因而每部分分成的圆心角 ,旋转的整数倍,就可以与自身重合.
【总结】本题考查了旋转对称图形的旋转角的求法.
【练习17】在这几个字母中,中心对称图形有___________个.
【难度】★★
【答案】3
【解析】中心对称图形要寻找对称中心,旋转后两部分重合,
故中心对称图形:;轴对称图形:,
故中心对称图形有3个.
【总结】本题考查了中心对称图形与轴对称图形的定义.
【练习18】如图,将腰长为的等腰直角沿直线翻转,则直角顶点走过的路径长为 ______________.
【难度】★★
【答案】.
【解析】由题可得:点C走过的路径为弧和弧,弧长公式,且弧=弧;
圆心角,,则弧,
所以直角顶点走过的 路径长为.
【总结】本题考查了旋转的性质及弧长公式的运用.
【练习19】当=________时,代数式的值等于.
【难度】★★
【答案】1.
【解析】由分母,分子,得:,故令,所以.
【总结】本题考查了分式值等于0的条件:分子为0,分母不为0.
【练习20】当时,关于的方程有增根.
【难度】★★
【答案】1.
【解析】由题意,知方程的增根是,即;
给方程两边同时乘以,得:
解得:,将代入,得:,
所以,当时,原方程有增根.
【总结】本题考查了分式方程产生增根的条件以及对增根的理解及运用.
【练习21】如果,则=______________.
【难度】★★
【答案】4.
【解析】.
【总结】本题考查了分式的运算及整体代入思想的运用.
【练习22】已知:如图,在正方形中,点在边上,将绕点按顺时针方 向旋转,与重合,那么旋转角等于_________度.
【难度】★★
【答案】.
【解析】∵四边形为正方形,
∴.
∵将绕点按顺时针方向旋转,与重合,
∴是旋转角,
∴旋转角等于.
【总结】本题考查了旋转的性质及旋转角的确定.
【练习23】如图,一块含有角()的直角三角板,在水平的桌面上绕 点按顺时针方向旋转到的位置,那么旋转角是________度.
【难度】★★
【答案】.
【解析】∵直角三角板,在水平的桌面上绕点按
顺时针方向旋转到的位置,
∴点的对应点就是点,则旋转角等于,
又∵在直角三角形中,∴,
∴.
【总结】本题考查了旋转角的定义及在旋转图形中旋转角大小的确定.
【练习24】若,则.
【难度】★★★
【答案】6
【解析】由,得:,
则.
【总结】本题考查了完全平方公式的公式变形及运用.
【练习25】已知,则.
【难度】★★★
【答案】.
【解析】由,得:,
所以,故.
【总结】本题考查了负整数指数幂的运算及整体代入思想的综合运用.
【练习26】下面是用棋子摆成的“上”字:
第一个“上”字需用6枚棋子,第二个“上”字需用10枚棋子,第三个“上”字需用14枚棋子,如果按照这样的规律继续摆下去,那么第n个“上”字需用 枚棋子.
【难度】★★★
【答案】.
【解析】不难发现后一个“上”字比前一个多4个棋子,等差数列列出代数式:
.
【总结】本题考查了列代数式的相关知识及找规律的问题.
【练习27】如图,已知正方形的边长为8,在上,且,是上的 一个动点,则的最小值是____________.
【难度】★★★
【答案】10
【解析】解:如图所示,连接、.
∵正方形ABCD, ∴点与点关于直线对称,
∴. 又∵正方形的边长为,, ∴.
根据勾股定理,可得:.
∵,
∴当、、三点在一条直线上时,有最小值,且最小值为.
【总结】本题考查了“和最小”的问题以及对称性的运用,难度较大,并且计算时运用了勾股定理,因此教师要选择性的讲解.
【练习28】分解因式:.
【难度】★
【答案】.
【解析】.
【总结】本题考查了因式分解中的分组分解法的运用.
【练习29】计算:.
【难度】★
【答案】1.
【解析】.
【总结】本题考查了积的乘方的逆用.
【练习30】如图,已知,按下列要求画出图形:
(1)作出绕点逆时针方向旋转后的;
(2)作出关于直线对称的.
【难度】★
【答案】见解析.
【解析】(1) (2)
【总结】本题考查了图形的旋转和对称,注意画图时找到关键点.
【练习31】如图, 画出方格上的小鱼图形向右平移4格,再向上平移3格后的图形;
【难度】★
【答案】见解析
【解析】找出原图形上的关键点先进行平移,
之后点连成线构图即可.
【总结】本题考查了平移的性质及画法.
【练习32】 如图,正六边形是由边长为2厘米的六个等边三角形拼成,那么图 中:
(1) 三角形沿着___________方向平移_________厘米能与三角形重合;
(2) 三角形绕着点______顺时针旋转________度后能与三角形重合;
(3) 三角形沿着所在直线翻折后能与________重合;
(4) 写一对中心对称的三角形:_________________________.
【难度】★★
【答案】(1)射线BO、2厘米;(2)O、120;
(3);(4).
【解析】(1)根据平移的性质即可得出答案;
(2)根据旋转的定义结合图形即可得出答案;
(3)根据轴对称的定义结合图形即可得出翻折后与重合
(4)根据中心对称的定义,写出一对即可.
【总结】本题考查了图形运动的三种方式,注意每种运动的特征.
【练习33】比较大小:,,,.
【难度】★★
【答案】.
【解析】因为,,
; 故.
【总结】本题考查了指数幂的运算以及大小比较.
【练习34】 分解因式:.
【难度】★★
【答案】.
【解析】.
【总结】本题考查了因式分解的公式法及换元思想的运用,注意分解要彻底.
【练习35】因式分解:.
【难度】★★
【答案】.
【解析】.
【总结】本题考查了因式分解的十字相乘法及整体换元思想,注意因式分解要彻底.
【练习36】 计算:(计算结果不含负整数指数幂).
【难度】★★
【答案】.
【解析】.
【总结】本题考查了分式的化简及平方差公式的运用
【练习37】计算:.
【难度】★★
【答案】.
【解析】原式.
【总结】本题考查了整数指数幂的运算,注意要按照运算顺序进行计算.
【练习38】若,为有理数,且,求的值.
【难度】★★
【答案】.
【解析】因为,所以;
所以,则.
【总结】本题考查了完全平方公式的运用及代数式的求值运算.
【练习39】先化简,再求值: 已知,求代数式的 值.
【难度】★★
【答案】.
【解析】由,得:.
故
,
将代入,则原式.
【总结】本题考查了分式的化简及求值运算,注意化简时要先分解因式再约分.
【练习40】计算:.
【难度】★★
【答案】.
【解析】.
【总结】本题考查了分式的除法运算,注意要先分解因式再约分.
【练习41】 计算:.
【难度】★★
【答案】.
【解析】.
【总结】本题考查了分式的混合运算,注意按照法则和运算顺进行计算.
【练习42】解方程:.
【难度】★★
【答案】.
【解析】去分母,得:,
解得:,
经检验,把代入最简公分母中:,
所以是原分式方程的解.
【总结】本题考查了分式方程的解法,注意解完之后一定要检验.
【练习43】已知都是正数,且,试证明分式的值总小于的值.
【难度】★★
【答案】见解析.
【解析】证明:,
∵均为正数,, ∴, ∴.
∵, ∴.
故的值总小于.
【总结】本题考查了利用作差法比较分式值的大小.
【练习44】某商厦的进货员在苏州发现一种应季羊绒衫,预计能畅销,就用元购进所 有羊绒衫,还急需倍这种服装,经人介绍又在杭州用元购进所有羊绒衫,只是 单价比苏州贵了四十元,商厦按每件元销售,销路很好,最后剩下的件按折售 完,问进货员在苏州和杭州分别购进羊绒衫多少件?这笔生意商厦盈利是多少?
【难度】★★
【答案】苏州进货200件,杭州进货400件,商厦共赢利86200元.
【解析】解:设进货员在苏州进货件,则在杭州进货件,商厦共赢利元;
由题意得:
解得:
经检验,是原方程的解,同时满足实际要求;
再结合题意
把代入,则.
答:在苏州进货200件,杭州进货400件,商厦共赢利86200元.
【总结】本题考查了分式方程在实际问题中的应用.
【练习45】利用平移知识求所示图形的周长.
【难度】★★
【答案】18.
【解析】由图可知,平移后会得到一个长方形,
长为5,宽为4,故周长为18.
【总结】本题考查了平移转化思想在求图形周长中的运用.
【练习46】如图,把图中的某两个小方格涂上阴影,使整个图形是以虚线为对称轴的轴对称 图形.
【难度】★★
【答案】见解析.
【解析】如图:
【总结】本题考查了利用轴对称图形的性质进行画图.
【练习47】如图,在长方形中,,,现将长方形向右平 移,再向下平移后到长方形的位置,
(1)用的代数式表示长方形ABCD与长方形的重叠部分的面积,这时应满 足怎样的条件?
(2)用的代数式表示六边形(阴影部分)的面积.
【难度】★★★
【答案】(1);(2).
【解析】(1)∵,,
∴重叠部分的长为,宽为,
∴重叠部分的面积为:
;∵,解得:;
∴应满足的条件是:;
(2).
【总结】本题考查了用字母表示数及阴影面积的求法.
【练习48】设为正整数,求证:.
【难度】★★★
【答案】见解析.
【解析】
=,
∵为正整数,∴;故原不等式得证.
【总结】本题考查了利用作差法比较分数大小及通过裂项求分数和的问题.
【练习49】已知,求整数.
【难度】★★★
【答案】.
【解析】①当指数时,底数,故;
②当底数时,有;
③当底数时,指数,为偶数,有;
所以均可以.
【总结】本题考查了幂的值为1的分类讨论.
【练习50】已知,求的值.
【难度】★★★
【答案】4016
【解析】原式.
【总结】本题考查了完全平方公式的变形:的运用.
【练习51】如图,已知等腰直角三角形ACB的边AC=BC=a,等腰直角三角形BED的 边 BE = DE = b,且,点C、B、E放置在一条直线上,联结AD.
(1)求三角形ABD的面积;
(2)如果点P是线段CE的中点,联结AP、DP得到三角形APD,求三角形APD的面积;
(3)(2)中的三角形APD与三角形ABD面积那个较大?大多少?
(结果都可用、代数式表示,并化简)
【难度】★★★
【答案】见解析.
【解析】(1)
;
(2)
;
(3),
∵,
∴.
【总结】本题考查了利用字母表示几何图形的面积,并且通过作差法比较两个分式的大小,综合性较强.
期末复习二
内容分析
知识结构
选择题
A
B
C
正六边形
等腰梯形
正三角形
正五边形
甲
乙
甲
乙
乙
甲
(2)
(1)
(3)
填空题
A
B
C
D
E
F
N
解答题
A
B
C
A
B
C
D
A′
B′
C′
D′
A
D
B
C
E
a
a
b
b
