沪科版八年级上册第14章全等三角形期末复习题(无答案)
文档属性
| 名称 | 沪科版八年级上册第14章全等三角形期末复习题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 417.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 10:29:15 | ||
图片预览

文档简介
第14章 全等三角形期末复习题
知识点一、全等三角形判定条件
1、在△ABC和△FED 中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件( )
A.AB=ED B.AB=FD
C.AC=FD D.∠A=∠F
2、在△ABC和△中,AB=,∠B=∠,补充条件后仍不一定能保证△ABC≌ △,则补充的这个条件是( )
A.BC= B.∠A=∠
C.AC= D.∠C=∠
知识点二、全等三角形的性质及应用
3.如图,△ABC≌△EBD,问∠1与∠2相等吗?若相等请证明, 若不相等说出为什么?
解析:由三角形全等,得到对应角相等,然后再沟通∠1和∠2之间的关系.
4.如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,
∠CDE=100°,∠DEB=10°,求∠AEC的度数.
知识点三、利用全等进行测量
5. 1805年,法国拿破仑率军与德军在莱茵河激战,德军在河北岸Q处,如图,因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸O处调整好自己的帽子,使视线恰好擦过帽舌边沿看到敌军兵营Q处,然后后退到B点,这时他的视点恰好能落在O处,于是他命令部下测量他脚站的B处与O点之间的距离,并下令按这个距离炮轰敌兵营,法军能命中吗?说明理由.
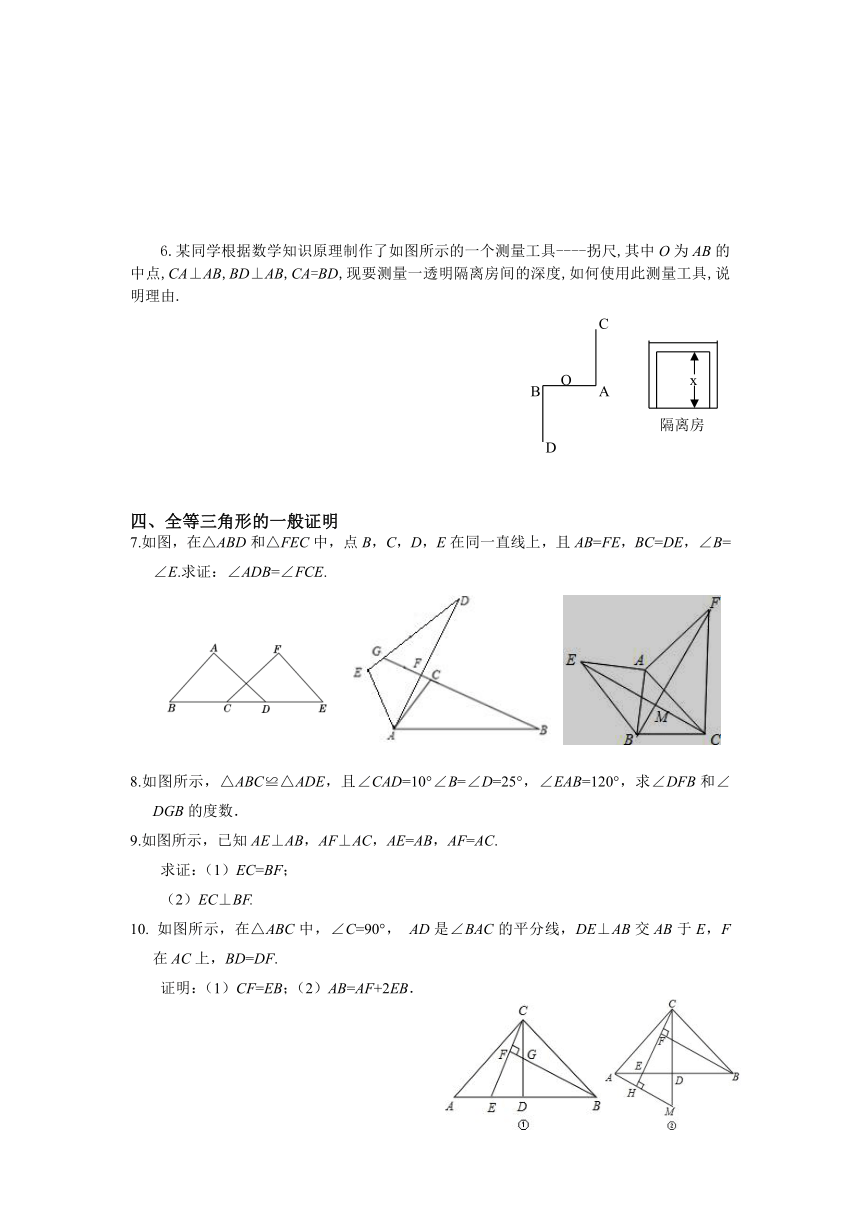
6.某同学根据数学知识原理制作了如图所示的一个测量工具----拐尺,其中O为AB的中点,CA⊥AB,BD⊥AB,CA=BD,现要测量一透明隔离房间的深度,如何使用此测量工具,说明理由.
四、全等三角形的一般证明
7.如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
8.如图所示,△ABC≌△ADE,且∠CAD=10°∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
9.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
求证:(1)EC=BF;
(2)EC⊥BF.
10. 如图所示,在△ABC中,∠C=90°, AD是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF.
证明:(1)CF=EB;(2)AB=AF+2EB.
11.如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC.
12.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)过点B作BF⊥CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)过点A作AH⊥CE,交CE的延长线于点H,并交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
五、全等三角形的探究题
13.全等三角形又叫合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形.假设△ABC和△A1B1C1是全等(合同)三角形,且点A与A1对应,点B与B1对应,点C与点C1对应,当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形,如图1;若运动方向相反,则称它们是镜面合同三角形,如图2.
(1) (2)
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中一个翻折180°,下列各组合同三角形中,是镜面合同三角形的是( ).
14.如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)试说明BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
15.如图所示,△ABC绕着点B旋转(顺时针)90°到△DBE,且∠ABC=90°.
⑴△ABC和△DBE是否全等?指出对应边和对应角;
⑵直线AC、直线DE有怎样的位置关系?
16.如图所示,在△ABC中, ∠C=90,AC=10㎝,BC=5㎝,一条线段PQ=AB,P,Q两点分别在AC和过A点且垂直于AC的射线上运动.问P点运动到AC上什么位置时, △ABC才能和△APQ全等?
17.如图(1),已知AB⊥BD,ED⊥BD,AB=CD,BC=DE.
(1)试判断AC与CE的位置关系,并说明理由.
(2)若将CD沿CB方向平移得到图(2)(3)(4)(5)的情形,其余条件不变,此时第(1)问中AC与CE的位置关系还成立吗?结论还成立吗?请说明理由.
18.能够互相重合的多边形叫做全等形,即如果两个多边形对应角相等,对应边相等,那么两个多边形一定全等。但判定两个三角形全等只需三组对应量相等即可,如SAS,SSS等,但如果要判定两个四边形全等仅有四组量对应相等是不够的,必须具备至少五组量对应相等.
(1)请写出两个四边形全等的一种判定方法(五组量对应相等);
(2)如图,简要说明你的判定方法是正确的;
(3)举例说明仅有四边对应相等的两个四边形不一定全等(画出图形并简要说明理由).
B
A
O
P
Q
C
A
B
D
O
x
隔离房
A
B
C
D
E
知识点一、全等三角形判定条件
1、在△ABC和△FED 中,已知∠C=∠D,∠B=∠E,要判定这两个三角形全等,还需要条件( )
A.AB=ED B.AB=FD
C.AC=FD D.∠A=∠F
2、在△ABC和△中,AB=,∠B=∠,补充条件后仍不一定能保证△ABC≌ △,则补充的这个条件是( )
A.BC= B.∠A=∠
C.AC= D.∠C=∠
知识点二、全等三角形的性质及应用
3.如图,△ABC≌△EBD,问∠1与∠2相等吗?若相等请证明, 若不相等说出为什么?
解析:由三角形全等,得到对应角相等,然后再沟通∠1和∠2之间的关系.
4.如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,
∠CDE=100°,∠DEB=10°,求∠AEC的度数.
知识点三、利用全等进行测量
5. 1805年,法国拿破仑率军与德军在莱茵河激战,德军在河北岸Q处,如图,因不知河宽,法军很难瞄准敌军,聪明的拿破仑站在南岸O处调整好自己的帽子,使视线恰好擦过帽舌边沿看到敌军兵营Q处,然后后退到B点,这时他的视点恰好能落在O处,于是他命令部下测量他脚站的B处与O点之间的距离,并下令按这个距离炮轰敌兵营,法军能命中吗?说明理由.
6.某同学根据数学知识原理制作了如图所示的一个测量工具----拐尺,其中O为AB的中点,CA⊥AB,BD⊥AB,CA=BD,现要测量一透明隔离房间的深度,如何使用此测量工具,说明理由.
四、全等三角形的一般证明
7.如图,在△ABD和△FEC中,点B,C,D,E在同一直线上,且AB=FE,BC=DE,∠B=∠E.求证:∠ADB=∠FCE.
8.如图所示,△ABC≌△ADE,且∠CAD=10°∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
9.如图所示,已知AE⊥AB,AF⊥AC,AE=AB,AF=AC.
求证:(1)EC=BF;
(2)EC⊥BF.
10. 如图所示,在△ABC中,∠C=90°, AD是∠BAC的平分线,DE⊥AB交AB于E,F在AC上,BD=DF.
证明:(1)CF=EB;(2)AB=AF+2EB.
11.如图所示,在△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC.
12.已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)过点B作BF⊥CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)过点A作AH⊥CE,交CE的延长线于点H,并交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
五、全等三角形的探究题
13.全等三角形又叫合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形.假设△ABC和△A1B1C1是全等(合同)三角形,且点A与A1对应,点B与B1对应,点C与点C1对应,当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形,如图1;若运动方向相反,则称它们是镜面合同三角形,如图2.
(1) (2)
两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中一个翻折180°,下列各组合同三角形中,是镜面合同三角形的是( ).
14.如图所示,A,D,E三点在同一直线上,且△BAD≌△ACE.
(1)试说明BD=DE+CE;
(2)△ABD满足什么条件时,BD∥CE?
15.如图所示,△ABC绕着点B旋转(顺时针)90°到△DBE,且∠ABC=90°.
⑴△ABC和△DBE是否全等?指出对应边和对应角;
⑵直线AC、直线DE有怎样的位置关系?
16.如图所示,在△ABC中, ∠C=90,AC=10㎝,BC=5㎝,一条线段PQ=AB,P,Q两点分别在AC和过A点且垂直于AC的射线上运动.问P点运动到AC上什么位置时, △ABC才能和△APQ全等?
17.如图(1),已知AB⊥BD,ED⊥BD,AB=CD,BC=DE.
(1)试判断AC与CE的位置关系,并说明理由.
(2)若将CD沿CB方向平移得到图(2)(3)(4)(5)的情形,其余条件不变,此时第(1)问中AC与CE的位置关系还成立吗?结论还成立吗?请说明理由.
18.能够互相重合的多边形叫做全等形,即如果两个多边形对应角相等,对应边相等,那么两个多边形一定全等。但判定两个三角形全等只需三组对应量相等即可,如SAS,SSS等,但如果要判定两个四边形全等仅有四组量对应相等是不够的,必须具备至少五组量对应相等.
(1)请写出两个四边形全等的一种判定方法(五组量对应相等);
(2)如图,简要说明你的判定方法是正确的;
(3)举例说明仅有四边对应相等的两个四边形不一定全等(画出图形并简要说明理由).
B
A
O
P
Q
C
A
B
D
O
x
隔离房
A
B
C
D
E
