2.1.1合情推理[1](34张PPT)
文档属性
| 名称 | 2.1.1合情推理[1](34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 11:29:18 | ||
图片预览







文档简介
(共34张PPT)
新课导入
铜、铁、铝、金、银等都能导电.
一切金属都能导电.
从所研究的对象全体中抽取一部分进行观测或试验以取得信息,从而对整体做出推断,是归纳推理.
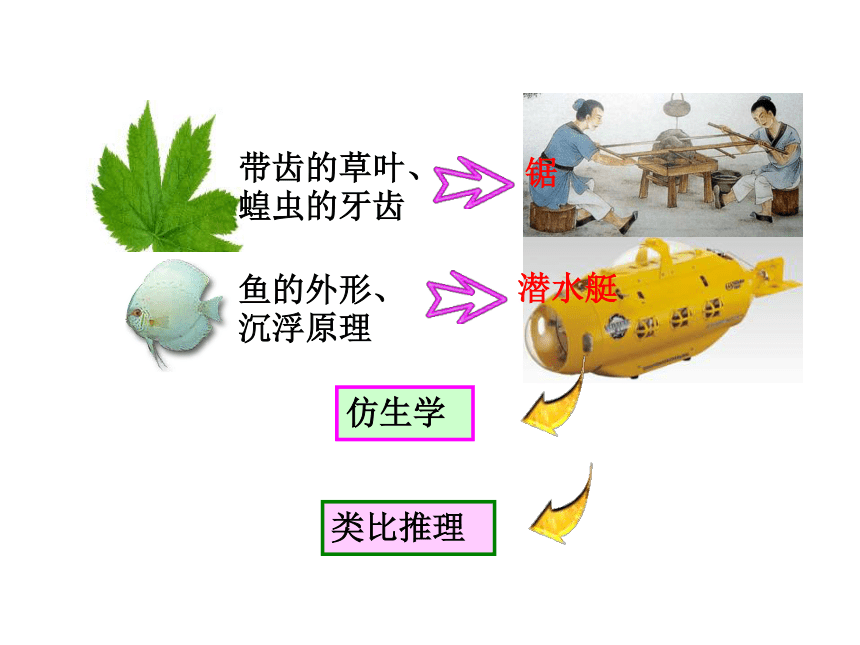
类比推理
带齿的草叶、蝗虫的牙齿
锯
鱼的外形、沉浮原理
潜水艇
仿生学
合情推理是指“合乎情理”的推理.数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论;证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向.
归纳推理——猜想
这些猜想是怎么得出的呢?
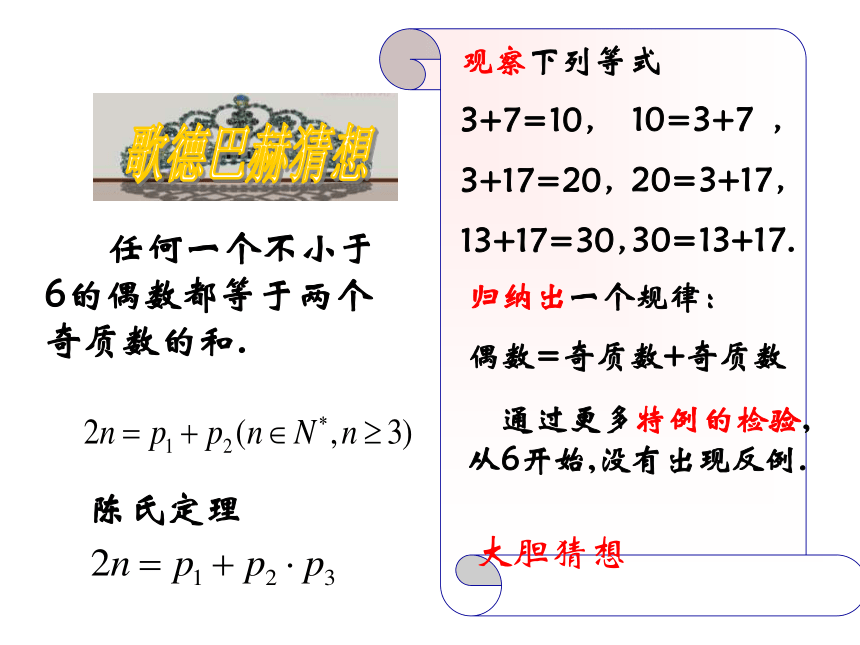
观察下列等式
3+7=10,
3+17=20,
13+17=30,
归纳出一个规律:
偶数=奇质数+奇质数
通过更多特例的检验,从6开始,没有出现反例.
大胆猜想
任何一个不小于6的偶数都等于两个奇质数的和.
10=3+7 ,
20=3+17,
30=13+17.
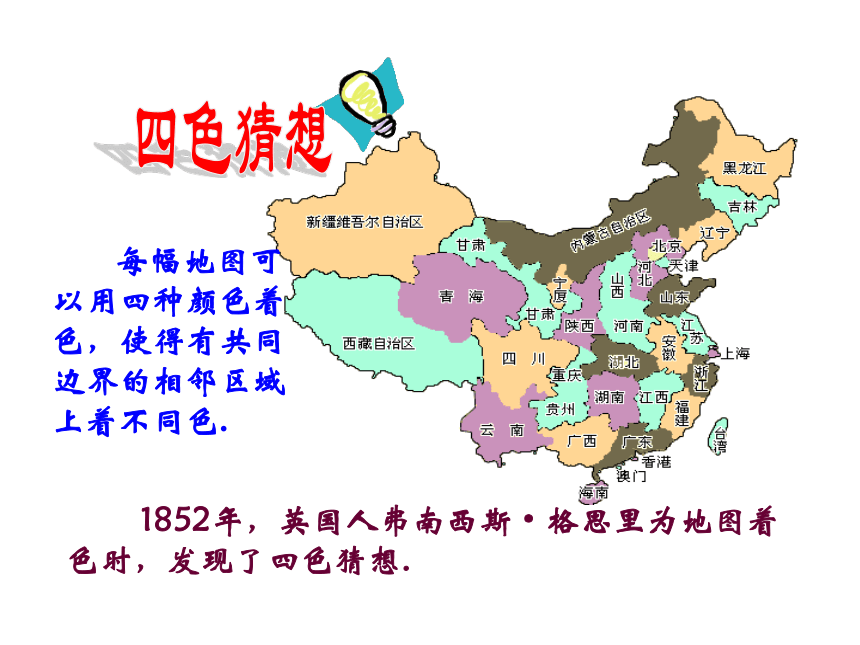
每幅地图可以用四种颜色着色,使得有共同边界的相邻区域上着不同色.
1852年,英国人弗南西斯·格思里为地图着色时,发现了四色猜想.
都是质数
例1
由某类事物的部分对象具有某些这些特征的推理,或者由个别事实概括出一般结论的推理称为归纳推理.
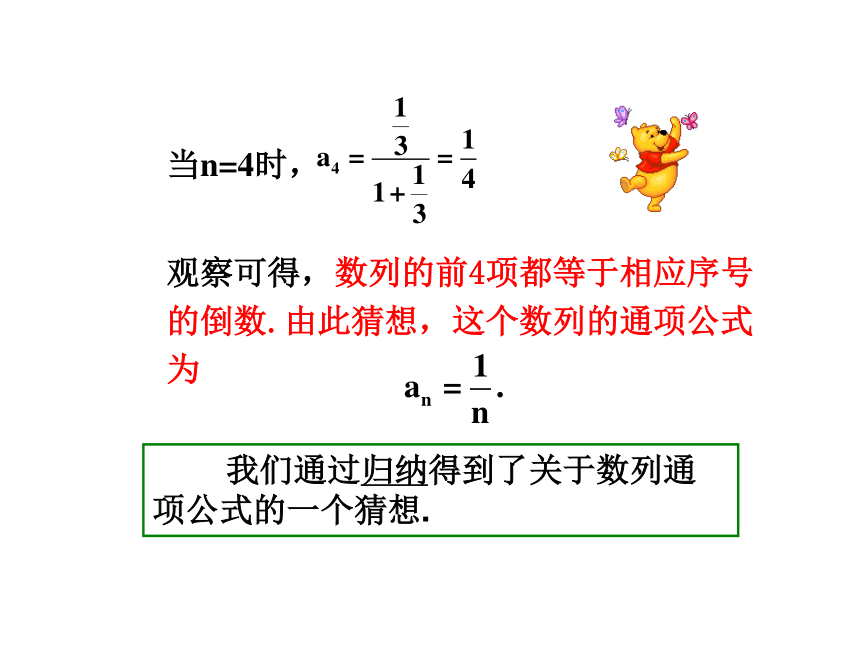
观察可得,数列的前4项都等于相应序号的倒数.由此猜想,这个数列的通项公式为
我们通过归纳得到了关于数列通项公式的一个猜想.
类比推理——火星上是否有生命
火星
地球
围绕太阳运行;
绕轴自转;
有大气层;
一年中有四季
变更;
温度适合地球
上某些
生物的生存;
对比两者某些相似特征.
火星也可能有生命的存在
试着类比球体和圆
球的类比概念和性质
圆的概念和性质
圆的周长
圆的面积
圆心与弦(非直径)中点的连线垂直于弦.
与圆心距离相等的两弦相等;与圆心距离不等的两弦不等,距圆心较近的弦较长
以点(a,b)为圆心,r为半径的圆的方程为
球的表面积
球的体积
球心与截面圆(非过球心截面圆)圆心连线垂直于截面圆
与球心距离相等的两截面圆面积相等;与球心距离不等的两截面圆面积不等,距圆心较近的截面圆面积较大.
以点(a,b,c)为球心,r为半径的球的方程为
“类比是一个伟大的引路人,求解立体几何问题往往有赖于平面几何中的类比问题.”
——数学家波利亚
“我珍视类比胜过任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密.”
——开普勒
例2
类比实数的加法和乘法,列出它们相似的运算性质.
由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.
分析:实数的加法和乘法都是由两个数参与的运算,都满足一定的运算律,都存在逆运算,而且“0”和“1”分别在加法和乘法中占有特殊的地位.因此我们可以从上述4个方面来类比这两种运算.
(2)从运算律的角度考虑,加法和乘法都满足交换律和结合律,即
解:(1)两个实数经过加法运算或乘法运算后,所得的结果仍然是一个实数.
从逆运算的角度考虑,二者都有逆运算,加法的逆运算是减法,乘法的逆运算是除法,这就使得方程
都有唯一解.
(4)在加法中,任意实数与0相加都不改变大小;乘法中的1与加法中的0类似,即任意实数与1的积都等于原来的数.即
你认为平面几何中的哪一类图形可以作为四面体的类比对象?
例3
类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.
分析:考虑到直角三角形的两条边互相垂直,所以我们可以选取有3个面两两垂直的四面体,作为直角三角形的类对比对象.
解:如图.我们知道,在 中.由勾股定理,得
于是,类比直角三角形的勾股定理,在四面体P-DEF中,我们猜想
推理过程概括:
从具体
问题出发
观察、分析
比较、联想
归纳、类比
提出猜想
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理.
例4
如图,有三跟针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
1. 每次只能移动1个金属片;
2. 较大的金属片不能放在较小的金属片上面.
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?
分析:我们从移动1,2,3,4个金属片的情形入手,探究其中的规律性,进而归纳出移动n个金属片所需的次数.
解:当n=1时,只需把金属片从1号针移到3号针.
把第1个金属片从1号针移动到2号针;
把第2个金属片从1号针移动到3号针;
把第1个金属片从2号针移动到3号针.
当n=2时,利用2号针做“中间针”移动:
当n=3时,把上面两个金属片作为一个整体,归结为n=2的情形移动:
把上面两个金属片从1号针移动到2号针;
把第3个金属片从1号针移动到3号针;
把上面两个金属片从2号针移动到3号针.
当n=4时,把上面3个金属片作为一个整体移动:
把上面3个金属片从1号针移动到2号针;
把第4个金属片从1号针移动到3号针;
把上面3个金属片从2号针移动到3号针.
至此,我们得到依次移动1,2,3,4个金属片所需的次数构成的数列:
1,3,7,15
由此我们猜想:
观察发现有如下规律:
探究:
把n个金属片从1号针移动
到3号针,怎样移动才能达到
最少的移动次数呢?
归纳:
对n个金属片都适用的移动方法.当移动n个金属片时,可分为以下3个步骤:
把上面(n-1)个金属片从1号针移动到2号针;
把第n个金属片从1号针移动到3号针;
把上面(n-1)个金属片从2号针移动到3号针.
那第(n-1)个金属片如何移动呢?
把上面(n-2)个金属片从1号针移动到2号针;
把第(n-1)个金属片从1号针移动到3号针;
把上面(n-2)个金属片从2号针移动到3号针.
类比推理
得到递推公式:
这是我们根据n=1,2,3,4时的移动方法,归纳推理出来.
合情推理的结果的正确与否,并不完全依赖于前提条件.
合情推理是冒险的、有争议的和暂时的.
——波利亚
在合情推理中,灵感也是一种重要的思维形式.
课堂小结
由某类事物的部分对象具有某些特征推出该类事物全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理称为归纳推理.
由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理.
新课导入
铜、铁、铝、金、银等都能导电.
一切金属都能导电.
从所研究的对象全体中抽取一部分进行观测或试验以取得信息,从而对整体做出推断,是归纳推理.
类比推理
带齿的草叶、蝗虫的牙齿
锯
鱼的外形、沉浮原理
潜水艇
仿生学
合情推理是指“合乎情理”的推理.数学研究中,得到一个新结论之前,合情推理常常能帮助我们猜测和发现结论;证明一个数学结论之前,合情推理常常能为我们提供证明的思路和方向.
归纳推理——猜想
这些猜想是怎么得出的呢?
观察下列等式
3+7=10,
3+17=20,
13+17=30,
归纳出一个规律:
偶数=奇质数+奇质数
通过更多特例的检验,从6开始,没有出现反例.
大胆猜想
任何一个不小于6的偶数都等于两个奇质数的和.
10=3+7 ,
20=3+17,
30=13+17.
每幅地图可以用四种颜色着色,使得有共同边界的相邻区域上着不同色.
1852年,英国人弗南西斯·格思里为地图着色时,发现了四色猜想.
都是质数
例1
由某类事物的部分对象具有某些这些特征的推理,或者由个别事实概括出一般结论的推理称为归纳推理.
观察可得,数列的前4项都等于相应序号的倒数.由此猜想,这个数列的通项公式为
我们通过归纳得到了关于数列通项公式的一个猜想.
类比推理——火星上是否有生命
火星
地球
围绕太阳运行;
绕轴自转;
有大气层;
一年中有四季
变更;
温度适合地球
上某些
生物的生存;
对比两者某些相似特征.
火星也可能有生命的存在
试着类比球体和圆
球的类比概念和性质
圆的概念和性质
圆的周长
圆的面积
圆心与弦(非直径)中点的连线垂直于弦.
与圆心距离相等的两弦相等;与圆心距离不等的两弦不等,距圆心较近的弦较长
以点(a,b)为圆心,r为半径的圆的方程为
球的表面积
球的体积
球心与截面圆(非过球心截面圆)圆心连线垂直于截面圆
与球心距离相等的两截面圆面积相等;与球心距离不等的两截面圆面积不等,距圆心较近的截面圆面积较大.
以点(a,b,c)为球心,r为半径的球的方程为
“类比是一个伟大的引路人,求解立体几何问题往往有赖于平面几何中的类比问题.”
——数学家波利亚
“我珍视类比胜过任何别的东西,它是我最可信赖的老师,它能揭示自然界的秘密.”
——开普勒
例2
类比实数的加法和乘法,列出它们相似的运算性质.
由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.
分析:实数的加法和乘法都是由两个数参与的运算,都满足一定的运算律,都存在逆运算,而且“0”和“1”分别在加法和乘法中占有特殊的地位.因此我们可以从上述4个方面来类比这两种运算.
(2)从运算律的角度考虑,加法和乘法都满足交换律和结合律,即
解:(1)两个实数经过加法运算或乘法运算后,所得的结果仍然是一个实数.
从逆运算的角度考虑,二者都有逆运算,加法的逆运算是减法,乘法的逆运算是除法,这就使得方程
都有唯一解.
(4)在加法中,任意实数与0相加都不改变大小;乘法中的1与加法中的0类似,即任意实数与1的积都等于原来的数.即
你认为平面几何中的哪一类图形可以作为四面体的类比对象?
例3
类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想.
分析:考虑到直角三角形的两条边互相垂直,所以我们可以选取有3个面两两垂直的四面体,作为直角三角形的类对比对象.
解:如图.我们知道,在 中.由勾股定理,得
于是,类比直角三角形的勾股定理,在四面体P-DEF中,我们猜想
推理过程概括:
从具体
问题出发
观察、分析
比较、联想
归纳、类比
提出猜想
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理.
例4
如图,有三跟针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
1. 每次只能移动1个金属片;
2. 较大的金属片不能放在较小的金属片上面.
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?
分析:我们从移动1,2,3,4个金属片的情形入手,探究其中的规律性,进而归纳出移动n个金属片所需的次数.
解:当n=1时,只需把金属片从1号针移到3号针.
把第1个金属片从1号针移动到2号针;
把第2个金属片从1号针移动到3号针;
把第1个金属片从2号针移动到3号针.
当n=2时,利用2号针做“中间针”移动:
当n=3时,把上面两个金属片作为一个整体,归结为n=2的情形移动:
把上面两个金属片从1号针移动到2号针;
把第3个金属片从1号针移动到3号针;
把上面两个金属片从2号针移动到3号针.
当n=4时,把上面3个金属片作为一个整体移动:
把上面3个金属片从1号针移动到2号针;
把第4个金属片从1号针移动到3号针;
把上面3个金属片从2号针移动到3号针.
至此,我们得到依次移动1,2,3,4个金属片所需的次数构成的数列:
1,3,7,15
由此我们猜想:
观察发现有如下规律:
探究:
把n个金属片从1号针移动
到3号针,怎样移动才能达到
最少的移动次数呢?
归纳:
对n个金属片都适用的移动方法.当移动n个金属片时,可分为以下3个步骤:
把上面(n-1)个金属片从1号针移动到2号针;
把第n个金属片从1号针移动到3号针;
把上面(n-1)个金属片从2号针移动到3号针.
那第(n-1)个金属片如何移动呢?
把上面(n-2)个金属片从1号针移动到2号针;
把第(n-1)个金属片从1号针移动到3号针;
把上面(n-2)个金属片从2号针移动到3号针.
类比推理
得到递推公式:
这是我们根据n=1,2,3,4时的移动方法,归纳推理出来.
合情推理的结果的正确与否,并不完全依赖于前提条件.
合情推理是冒险的、有争议的和暂时的.
——波利亚
在合情推理中,灵感也是一种重要的思维形式.
课堂小结
由某类事物的部分对象具有某些特征推出该类事物全部对象都具有这些特征的推理,或者由个别事实概括出一般结论的推理称为归纳推理.
由两类对象具有某些类似特征和其中一类对象的某些已知特征,推出另一类对象也具有这些特征的推理称为类比推理.
归纳推理和类比推理都是根据已有的事实,经过观察、分析、比较、联想,再进行归纳、类比,然后提出猜想的推理,我们把它们统称为合情推理.
