2.2.1综合法与分析法[1](33张PPT)
文档属性
| 名称 | 2.2.1综合法与分析法[1](33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 838.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
2.2.1综合法和分析法
综合法和分析法,是直接证明中最基本的两种证明方法,也是解决数学问题时常用的思维方式.
新课导入
在以前的学习中,大家已经能应用综合法、分析法证明数学命题,但是对这些证明方法的内涵和特点,大家又了解多少呢?
本节课我们对综合法和分析法这些证明方法进行较系统的学习.
综合法
不等式:
(a>0,b>0)的证明.
运用以前学过的数学知识,大家自己证明试试看!
回忆…
动动脑
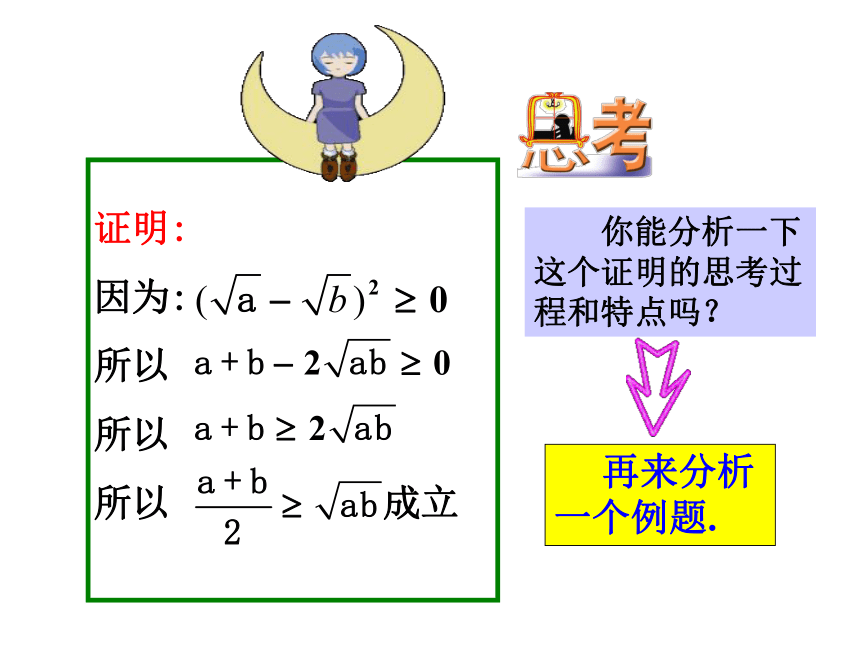
你能分析一下这个证明的思考过程和特点吗?
证明:
因为:
所以
所以
所以 成立
再来分析一个例题.
例:
已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
提示
首先,分析待证不等式的特点:不等式的右端是3个数a,b,c乘积的4倍,左端为两项之和,其中每一项都是一个数与另两个数的平方和之积.据此,只要把两个数的平方和转化为这两个数的积的形式,就能使不等式左、右两端具有相同的形式.
其次,寻找转化的依据及证明中要用的其他知识:应用不等式x2+y2≥2xy就能实现转化,不等式的基本性质是证明的依据.
最后,给出具体证明:由 b2+c2 ≥ 2ab及条件a>0,
得a(b2+c2) ≥ 2abc;
类似地,得b(c2+a2) ≥ 2abc.
从而有 a(b2+c2)+b(c2+a2) ≥ 4abc.
证明:
∵ b2+c2 ≥ 2bc,a>0
∴ a(b2+c2) ≥2abc.
又∵ c2+b2 ≥ 2bc,b>0
∴ b(c2+a2) ≥ 2abc.
∴ a(b2+c2)+b(c2+a2) ≥ 4abc.
探究
思考…
这些证明过程有什么相似点?
这些证明过程都是从已知条件和某些数学定义、公理、定理等出发,通过推理推导出所要的结论.
知识要点
一般地,利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.其特点是“由因导果”.
则综合法可用框图表示如下:
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
…
你能用框图表示综合法吗?
例题1
在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证△ABC为等边三角形.
分析
将A,B,C成等差数列,转化为符号语言就是2B=A+C;
此时,如果能把角和边统一起来,那么就可以进一步寻找角和边之间的关系,进而判断三角形的形状,余弦定理正好满足要求.于是,可以用余弦定理为工具进行证明.
a,b,c成等比数列转化为符号语言就是
A,B,C为△ABC的内角,这是一个隐含条件,即A+B+C=180°;
证明:
由A,B,C成等差数列,有
2B=A+C.
①
因为A,B,C为△ABC的内角,所以
A+B+C=180°.
②
③
由a,b,c成等比数列,有
④
由
①
②,得
①
②,得
由
①
②,得
由余弦定理及③,可得
再由④,得
即
因此
a=c.
从而
A=C.
⑤
由
②
③
,得
所以△ABC为等边三角形.
注意
解决数学问题时,往往要先做语言的转换,如把文字语言转换成符号语言,或把符号语言转换成图形语言等.还要通过细致的分析,把其中的隐含条件明确表示出来.
⑤
分析法
不等式:
(a>0,b>0)的证明.
动动脑
大家想一想,除了综合法,还有别的证明方法吗?
证明:要证
只需证:
只需证:
只需证:
因为: 成立
所以 成立
类比综合法,你能分析一下这个证明的思考过程和特点吗?
要证明结论成立,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止.
这类证法的特点是:
这就是另一种证明方法——分析法.
知识要点
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
特点:执果索因.
类似综合法,我们也可以后框图来表示分析法:
得到一个明显成立的结论
…
分析法的适用范围:
当已知条件与结论之间的联系不够明显、直接,证明中需要用哪些知识不太明确具体时,往往采用从结论出发,结合已知条件,逐步反推,寻求使当前命题成立的充分条件的方法.
注意
例题2
分析
从待证不等式不易发现证明的出发点,因此我们直接从待证不等式出发,分析其成立的充分条件.
证明:
只需证
展开得
只需证
因为 和 都是正数,所以要证
只需证
21<25.
因为21<25成立,所以 成立.
反思
在本例中,如果我们从“21<25”出发,逐步倒推回去,就可以用综合法证出结论.但由于我们很难想到从“21<25”入手,所以用综合法比较困难.
请对综合法与分析法进行比较,说出它们各自的特点.回顾以往的数学学习,说说你对这两种证明方法的新认识.
综合法就是利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立.
分析法最大的特点就是执果索因.
注意
事实上,在解决问题时,我们把综合法和分析法结合起来使用:根据条件的结构特点去转化结论,得到中间结论 ;根据结论的结构特点去转化条件,得到中间结论 .若由 可以推出 成立,就可以证明结论成立.
例题3
求证
分析
比较已知条件和结论,发现结论中没有 出现角 ,因此第一步工作可以从已知条件中消去 .
观察已知条件的结构特点,发现其中蕴含数量关系 ,于是,由(1) ×(1)-2(2)得 .把它与结论相比较,发现角相同,但函数名不同.
于是尝试转化结论:统一函数名称,即把正切函数化为正(余)弦函数.把结论转化为
再与 比较,发现只要把 的角的余弦转化为正弦,就能达到目的.
证明:
(3)
由于上式与③相同,于是问题得证.
课堂小结
1.综合法的概念:
一般地,利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.
2.分析法的概念:
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
3.分析法的适用范围:
当已知条件与结论之间的联系不够明显、直接,证明中需要用哪些知识不太明确具体时,往往采用从结论出发,结合已知条件,逐步反推,寻求使当前命题成立的充分条件的方法.
4.在证明数学问题时,通常把综合法和分析法结合起来使用.
2.2.1综合法和分析法
综合法和分析法,是直接证明中最基本的两种证明方法,也是解决数学问题时常用的思维方式.
新课导入
在以前的学习中,大家已经能应用综合法、分析法证明数学命题,但是对这些证明方法的内涵和特点,大家又了解多少呢?
本节课我们对综合法和分析法这些证明方法进行较系统的学习.
综合法
不等式:
(a>0,b>0)的证明.
运用以前学过的数学知识,大家自己证明试试看!
回忆…
动动脑
你能分析一下这个证明的思考过程和特点吗?
证明:
因为:
所以
所以
所以 成立
再来分析一个例题.
例:
已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc
提示
首先,分析待证不等式的特点:不等式的右端是3个数a,b,c乘积的4倍,左端为两项之和,其中每一项都是一个数与另两个数的平方和之积.据此,只要把两个数的平方和转化为这两个数的积的形式,就能使不等式左、右两端具有相同的形式.
其次,寻找转化的依据及证明中要用的其他知识:应用不等式x2+y2≥2xy就能实现转化,不等式的基本性质是证明的依据.
最后,给出具体证明:由 b2+c2 ≥ 2ab及条件a>0,
得a(b2+c2) ≥ 2abc;
类似地,得b(c2+a2) ≥ 2abc.
从而有 a(b2+c2)+b(c2+a2) ≥ 4abc.
证明:
∵ b2+c2 ≥ 2bc,a>0
∴ a(b2+c2) ≥2abc.
又∵ c2+b2 ≥ 2bc,b>0
∴ b(c2+a2) ≥ 2abc.
∴ a(b2+c2)+b(c2+a2) ≥ 4abc.
探究
思考…
这些证明过程有什么相似点?
这些证明过程都是从已知条件和某些数学定义、公理、定理等出发,通过推理推导出所要的结论.
知识要点
一般地,利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.其特点是“由因导果”.
则综合法可用框图表示如下:
用P表示已知条件、已有的定义、公理、定理等,Q表示所要证明的结论.
…
你能用框图表示综合法吗?
例题1
在△ABC中,三个内角A、B、C对应的边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列,求证△ABC为等边三角形.
分析
将A,B,C成等差数列,转化为符号语言就是2B=A+C;
此时,如果能把角和边统一起来,那么就可以进一步寻找角和边之间的关系,进而判断三角形的形状,余弦定理正好满足要求.于是,可以用余弦定理为工具进行证明.
a,b,c成等比数列转化为符号语言就是
A,B,C为△ABC的内角,这是一个隐含条件,即A+B+C=180°;
证明:
由A,B,C成等差数列,有
2B=A+C.
①
因为A,B,C为△ABC的内角,所以
A+B+C=180°.
②
③
由a,b,c成等比数列,有
④
由
①
②,得
①
②,得
由
①
②,得
由余弦定理及③,可得
再由④,得
即
因此
a=c.
从而
A=C.
⑤
由
②
③
,得
所以△ABC为等边三角形.
注意
解决数学问题时,往往要先做语言的转换,如把文字语言转换成符号语言,或把符号语言转换成图形语言等.还要通过细致的分析,把其中的隐含条件明确表示出来.
⑤
分析法
不等式:
(a>0,b>0)的证明.
动动脑
大家想一想,除了综合法,还有别的证明方法吗?
证明:要证
只需证:
只需证:
只需证:
因为: 成立
所以 成立
类比综合法,你能分析一下这个证明的思考过程和特点吗?
要证明结论成立,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止.
这类证法的特点是:
这就是另一种证明方法——分析法.
知识要点
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
特点:执果索因.
类似综合法,我们也可以后框图来表示分析法:
得到一个明显成立的结论
…
分析法的适用范围:
当已知条件与结论之间的联系不够明显、直接,证明中需要用哪些知识不太明确具体时,往往采用从结论出发,结合已知条件,逐步反推,寻求使当前命题成立的充分条件的方法.
注意
例题2
分析
从待证不等式不易发现证明的出发点,因此我们直接从待证不等式出发,分析其成立的充分条件.
证明:
只需证
展开得
只需证
因为 和 都是正数,所以要证
只需证
21<25.
因为21<25成立,所以 成立.
反思
在本例中,如果我们从“21<25”出发,逐步倒推回去,就可以用综合法证出结论.但由于我们很难想到从“21<25”入手,所以用综合法比较困难.
请对综合法与分析法进行比较,说出它们各自的特点.回顾以往的数学学习,说说你对这两种证明方法的新认识.
综合法就是利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立.
分析法最大的特点就是执果索因.
注意
事实上,在解决问题时,我们把综合法和分析法结合起来使用:根据条件的结构特点去转化结论,得到中间结论 ;根据结论的结构特点去转化条件,得到中间结论 .若由 可以推出 成立,就可以证明结论成立.
例题3
求证
分析
比较已知条件和结论,发现结论中没有 出现角 ,因此第一步工作可以从已知条件中消去 .
观察已知条件的结构特点,发现其中蕴含数量关系 ,于是,由(1) ×(1)-2(2)得 .把它与结论相比较,发现角相同,但函数名不同.
于是尝试转化结论:统一函数名称,即把正切函数化为正(余)弦函数.把结论转化为
再与 比较,发现只要把 的角的余弦转化为正弦,就能达到目的.
证明:
(3)
由于上式与③相同,于是问题得证.
课堂小结
1.综合法的概念:
一般地,利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法.
2.分析法的概念:
一般地,从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止,这种证明的方法叫做分析法.
3.分析法的适用范围:
当已知条件与结论之间的联系不够明显、直接,证明中需要用哪些知识不太明确具体时,往往采用从结论出发,结合已知条件,逐步反推,寻求使当前命题成立的充分条件的方法.
4.在证明数学问题时,通常把综合法和分析法结合起来使用.
