二项式定理(一)教案[1]
图片预览

文档简介
镇原县第二中学教案 自省明德 自胜成学
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
学 海 千 秋 勤 汲 取 心 田 万 亩 好 耕 耘1
镇原二中数学组信息化教学教案
课 题 §1.3.1 二项式定理
授课地点 高二(9)教室 授课班级 高二(9)班 授课时间 2018 年 5 月 15 日
授课类型 新授课 课时 第一课时 授课教师 王玥儒
教学目标
知识与技能
(1)理解二项式定理是代数乘法公式的推广.
(2)理解并掌握二项式定理及相关定义.
过程与方法
通过学生参与和探究二项式定理的形成过程,培养学生观察、分析、概括的能力,以
及化归的意识与方法迁移的能力,体会从特殊到一般的思维方式.
情感与价值
培养学生的自主探究意识,合作精神,体验二项式定理的发现和创造历程,体会数学
语言的简洁和严谨.
教材分析
教学重点 用计数原理分析得到二项式定理及通项公式
教学难点 用计数原理分析二项式的展开过程,发现二项式展开成单项式之和时各项系数的规律.
学法指导
1、问题诱导→启发讨论→归纳抽象→总结规律→引用延伸。
2、把自己易忘、易出错的疑难问题以及解题方法规律,及时整理在解题本,多复习记忆。
教学方法 启发、引导、讨论.
教 学 过 程 学生活动
先
学
自
研
互
动
一、前提测评
当 n=2,3 时,写出
nba )( ? 的展开式。
2)( ba ? =_______________________________________
3)( ba ? = ______________________________________
思考:
1 展开式中有哪些类型的项?这些类型的项是如何得到的?
2 展开式中各项的系数代表什么?
二、教学过程
(一)、提出问题,引入课题
二项式定理研究的是
nba )( ? 的展开式,如: 222 2)( bababa ???? ,
32233 33)( babbaaba ????? 那么 nba )( ? 的展开式是什么?
(二)引导探究,发现规律
2)( ba ? 、 3)( ba ? 展开式的再认识
探究 1:不运算 3)( ba ? ,能否回答下列问题(请以两人为一小组进行讨论):
(1) 合并同类项之前展开式有多少项?
(2) 展开式中有哪些不同的项?
(3) 各项的系数为多少?
(4)根据上述三个问题,你能否从计数原理角度得出 2)( ba ? 、 3)( ba ? 的展开式?
探究 2:仿照上述过程,请你推导 4)( ba ? 的展开式.
(1)分组讨论,互动探究。
(2)用多项式乘法再验证。
(3)写出结果。
探究 3:仿照上述过程,猜想 nba )( ? 的展开式.
)()( *110 NnbCbaCbaCaCba nnn
kknk
n
n
n
n
n
n ???????? ?? ??
自学自研
自主探究
比较异同
总结归纳
探
究
(三) 形成定理,说理证明
证明:
nba )( ? 是 n 个 )( ba ? 相乘,每个 )( ba ? 在相乘时,有两种选择,选 a或选 b,由分步
计数原理可知展开式共有
n2 项(包括同类项),其中每一项都是 kkn ba ? ),1,0( nk ?? 的形式,
对于每一项
kkn ba ? ,它是由 k 个 )( ba ? 选了 b,n-k 个 )( ba ? 选了 a 得到的,它出现的次数
相当于从 n 个 )( ba ? 中取 k 个 b 的组合数 knC ,将它们合并同类项,就得二项展开式,这就是
二项式定理.
(四) 熟悉定理,掌握特征
0 1( ) ( )n n n r n r r n nn n n na b C a C a b C a b C b n N
? ?? ? ? ? ? ? ? ?? ? ,
这个公式所表示的规律叫二项式定理,等式的左边叫做二项式;等式的右边叫做二项展开式;
二项式定理的公式特征:(由学生归纳,让学生熟悉公式)
1. 项数:共有 ?n 1项.
2. 次数:字母 a 按降幂排列,次数由 n 递减到 0;字母 b 按升幂排列,次数由 0 递增到 n.
各项的次数都等于 n.
3. 二项式系数: 依次为
n
n
k
nnnn CCCCC ,,,,,,
210 ?? ,这里 ),,1,0( nkC kn ???? 称为二项式系数.
4. 二项展开式的通项: 式中的
kknk
n baC
?
叫做二项展开式的通项. 用 1?k
T
表示.
即通项为展开式的第 ?k 1项: 1?kT =
kknk
n baC
?
认真思考
分析整合
归纳总结
理解记忆
精
讲
例 1、 求
6)12(
x
x ? 的展开式.
解:分析:先化简再运用公式
6
3
66 )12(1)12()12( ????? x
xx
x
x
x
])2()2()2()2()2()2[(1 6
6
5
6
24
6
33
6
42
6
51
6
6
3 CCCCCC xxxxxxx ???????
)126415820161532664(1 234563 ???????????? xxxxxxx
.1126016024019264 32
23
xxx
xxx ???????
思考:1、展开式的第3项的系数是多少?
2、展开式的第3项的二项式系数是多少?
例 2、(1)求(1+2x)7 的展开式的第 4 项的系数
所以展开式第 4 项的系数是 280
? ? .12 3
9
的系数的展开式中求 x
x
x ?
?
?
?
?
? ?
T3+1=C73?17-3?(2x)3
=35×23×x3
=280x3
静听思考
观察回答
积极思考
(1)解: (1+2x)
7
的展开式的第 4 项是
镇原县第二中学教案 自省明德 自胜成学
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
学 海 千 秋 勤 汲 取 心 田 万 亩 好 耕 耘2
释
疑
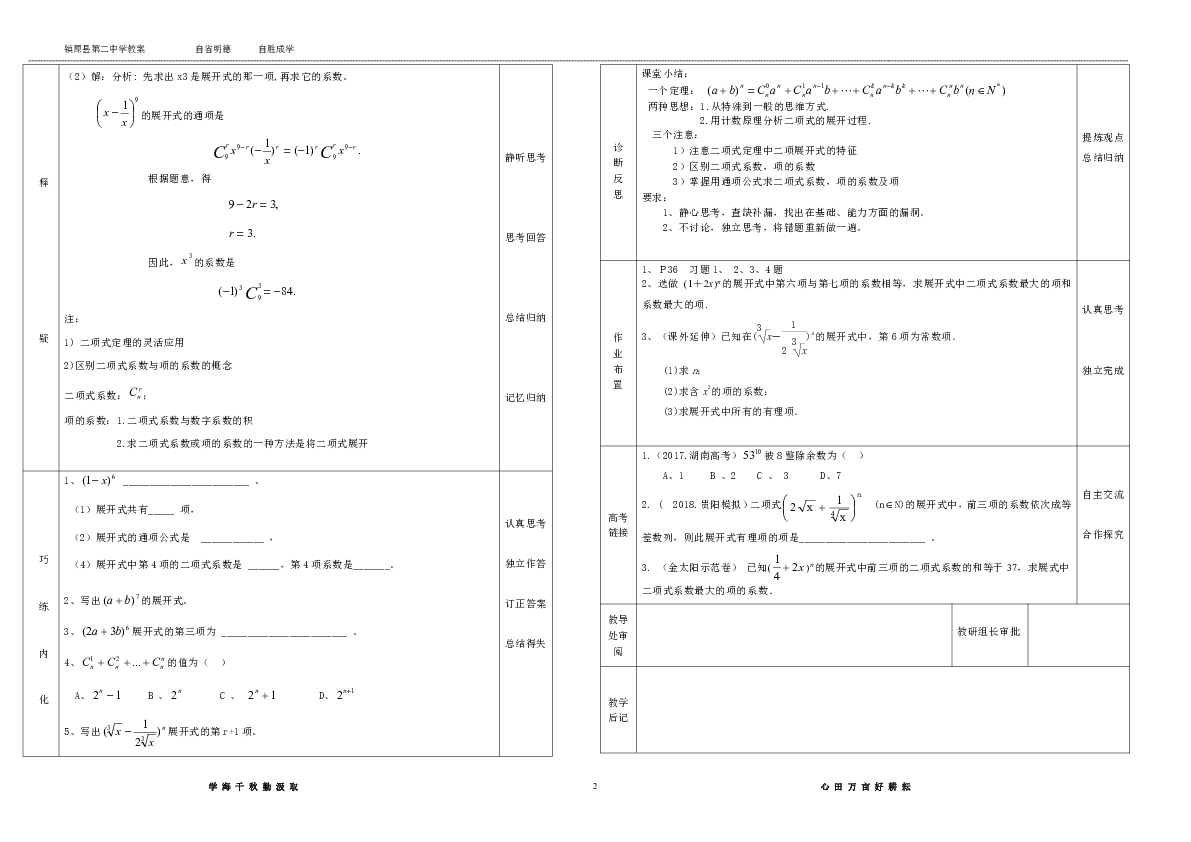
(2)解:分析: 先求出 x3 是展开式的那一项,再求它的系数。
91
?
?
?
?
?
? ?
x
x 的展开式的通项是
.)1()1( 9
9
9
9
rrrrrr x
x
x CC ?? ???
根据题意,得
,329 ?? r
.3?r
因此,
3x 的系数是
.84)1( 3
9
3 ??? C
注:
1) 二项式定理的灵活应用
2)区别二项式系数与项的系数的概念
二项式系数:
r
nC ;
项的系数:1.二项式系数与数字系数的积
2.求二项式系数或项的系数的一种方法是将二项式展开
静听思考
思考回答
总结归纳
记忆归纳
巧
练
内
化
1、
6)1( x? ________________________ 。
(1)展开式共有_____ 项,
(2)展开式的通项公式是 ____________ ,
(4)展开式中第 4 项的二项式系数是 ______,第 4 项系数是_______。
2、写出
7)( ba ? 的展开式。
3、
6)32( ba ? 展开式的第三项为 ________________________ 。
4、
n
nnn CCC ??? ...
21
的值为( )
A、 12 ?n B 、 n2 C 、 12 ?n D、 12 ?n
5、写出
n
x
x )
2
1(
3
3 ? 展开式的第 r+1 项。
认真思考
独立作答
订正答案
总结得失
诊
断
反
思
课堂小结:
一个定理: )()( *110 NnbCbaCbaCaCba nnn
kknk
n
n
n
n
n
n ???????? ?? ??
两种思想:1.从特殊到一般的思维方式.
2.用计数原理分析二项式的展开过程.
三个注意:
1)注意二项式定理中二项展开式的特征
2)区别二项式系数,项的系数
3)掌握用通项公式求二项式系数,项的系数及项
要求:
1、静心思考,查缺补漏,找出在基础、能力方面的漏洞。
2、不讨论,独立思考,将错题重新做一遍。
提炼观点
总结归纳
作
业
布
置
1、P36 习题 1、 2、3、4 题
2、选做 (1+2x)n的展开式中第六项与第七项的系数相等,求展开式中二项式系数最大的项和
系数最大的项.
3、(课外延伸)已知在(
3
x-
1
2
3
x
)
n
的展开式中,第 6项为常数项.
(1)求 n;
(2)求含 x2的项的系数;
(3)求展开式中所有的有理项.
认真思考
独立完成
高考
链接
1.(2017.湖南高考)
1053 被 8 整除余数为( )
A、1 B 、2 C 、 3 D、7
2. ( 2018.贵阳模拟)二项式
n
4 x
1x2 ?
?
?
?
?
? ? (n?N)的展开式中,前三项的系数依次成等
差数列,则此展开式有理项的项是________________________ 。
3. (金太阳示范卷) 已知(
1 2
4
x? )n的展开式中前三项的二项式系数的和等于 37,求展式中
二项式系数最大的项的系数.
自主交流
合作探究
教导
处审
阅
教研组长审批
教学
后记
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
学 海 千 秋 勤 汲 取 心 田 万 亩 好 耕 耘1
镇原二中数学组信息化教学教案
课 题 §1.3.1 二项式定理
授课地点 高二(9)教室 授课班级 高二(9)班 授课时间 2018 年 5 月 15 日
授课类型 新授课 课时 第一课时 授课教师 王玥儒
教学目标
知识与技能
(1)理解二项式定理是代数乘法公式的推广.
(2)理解并掌握二项式定理及相关定义.
过程与方法
通过学生参与和探究二项式定理的形成过程,培养学生观察、分析、概括的能力,以
及化归的意识与方法迁移的能力,体会从特殊到一般的思维方式.
情感与价值
培养学生的自主探究意识,合作精神,体验二项式定理的发现和创造历程,体会数学
语言的简洁和严谨.
教材分析
教学重点 用计数原理分析得到二项式定理及通项公式
教学难点 用计数原理分析二项式的展开过程,发现二项式展开成单项式之和时各项系数的规律.
学法指导
1、问题诱导→启发讨论→归纳抽象→总结规律→引用延伸。
2、把自己易忘、易出错的疑难问题以及解题方法规律,及时整理在解题本,多复习记忆。
教学方法 启发、引导、讨论.
教 学 过 程 学生活动
先
学
自
研
互
动
一、前提测评
当 n=2,3 时,写出
nba )( ? 的展开式。
2)( ba ? =_______________________________________
3)( ba ? = ______________________________________
思考:
1 展开式中有哪些类型的项?这些类型的项是如何得到的?
2 展开式中各项的系数代表什么?
二、教学过程
(一)、提出问题,引入课题
二项式定理研究的是
nba )( ? 的展开式,如: 222 2)( bababa ???? ,
32233 33)( babbaaba ????? 那么 nba )( ? 的展开式是什么?
(二)引导探究,发现规律
2)( ba ? 、 3)( ba ? 展开式的再认识
探究 1:不运算 3)( ba ? ,能否回答下列问题(请以两人为一小组进行讨论):
(1) 合并同类项之前展开式有多少项?
(2) 展开式中有哪些不同的项?
(3) 各项的系数为多少?
(4)根据上述三个问题,你能否从计数原理角度得出 2)( ba ? 、 3)( ba ? 的展开式?
探究 2:仿照上述过程,请你推导 4)( ba ? 的展开式.
(1)分组讨论,互动探究。
(2)用多项式乘法再验证。
(3)写出结果。
探究 3:仿照上述过程,猜想 nba )( ? 的展开式.
)()( *110 NnbCbaCbaCaCba nnn
kknk
n
n
n
n
n
n ???????? ?? ??
自学自研
自主探究
比较异同
总结归纳
探
究
(三) 形成定理,说理证明
证明:
nba )( ? 是 n 个 )( ba ? 相乘,每个 )( ba ? 在相乘时,有两种选择,选 a或选 b,由分步
计数原理可知展开式共有
n2 项(包括同类项),其中每一项都是 kkn ba ? ),1,0( nk ?? 的形式,
对于每一项
kkn ba ? ,它是由 k 个 )( ba ? 选了 b,n-k 个 )( ba ? 选了 a 得到的,它出现的次数
相当于从 n 个 )( ba ? 中取 k 个 b 的组合数 knC ,将它们合并同类项,就得二项展开式,这就是
二项式定理.
(四) 熟悉定理,掌握特征
0 1( ) ( )n n n r n r r n nn n n na b C a C a b C a b C b n N
? ?? ? ? ? ? ? ? ?? ? ,
这个公式所表示的规律叫二项式定理,等式的左边叫做二项式;等式的右边叫做二项展开式;
二项式定理的公式特征:(由学生归纳,让学生熟悉公式)
1. 项数:共有 ?n 1项.
2. 次数:字母 a 按降幂排列,次数由 n 递减到 0;字母 b 按升幂排列,次数由 0 递增到 n.
各项的次数都等于 n.
3. 二项式系数: 依次为
n
n
k
nnnn CCCCC ,,,,,,
210 ?? ,这里 ),,1,0( nkC kn ???? 称为二项式系数.
4. 二项展开式的通项: 式中的
kknk
n baC
?
叫做二项展开式的通项. 用 1?k
T
表示.
即通项为展开式的第 ?k 1项: 1?kT =
kknk
n baC
?
认真思考
分析整合
归纳总结
理解记忆
精
讲
例 1、 求
6)12(
x
x ? 的展开式.
解:分析:先化简再运用公式
6
3
66 )12(1)12()12( ????? x
xx
x
x
x
])2()2()2()2()2()2[(1 6
6
5
6
24
6
33
6
42
6
51
6
6
3 CCCCCC xxxxxxx ???????
)126415820161532664(1 234563 ???????????? xxxxxxx
.1126016024019264 32
23
xxx
xxx ???????
思考:1、展开式的第3项的系数是多少?
2、展开式的第3项的二项式系数是多少?
例 2、(1)求(1+2x)7 的展开式的第 4 项的系数
所以展开式第 4 项的系数是 280
? ? .12 3
9
的系数的展开式中求 x
x
x ?
?
?
?
?
? ?
T3+1=C73?17-3?(2x)3
=35×23×x3
=280x3
静听思考
观察回答
积极思考
(1)解: (1+2x)
7
的展开式的第 4 项是
镇原县第二中学教案 自省明德 自胜成学
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
学 海 千 秋 勤 汲 取 心 田 万 亩 好 耕 耘2
释
疑
(2)解:分析: 先求出 x3 是展开式的那一项,再求它的系数。
91
?
?
?
?
?
? ?
x
x 的展开式的通项是
.)1()1( 9
9
9
9
rrrrrr x
x
x CC ?? ???
根据题意,得
,329 ?? r
.3?r
因此,
3x 的系数是
.84)1( 3
9
3 ??? C
注:
1) 二项式定理的灵活应用
2)区别二项式系数与项的系数的概念
二项式系数:
r
nC ;
项的系数:1.二项式系数与数字系数的积
2.求二项式系数或项的系数的一种方法是将二项式展开
静听思考
思考回答
总结归纳
记忆归纳
巧
练
内
化
1、
6)1( x? ________________________ 。
(1)展开式共有_____ 项,
(2)展开式的通项公式是 ____________ ,
(4)展开式中第 4 项的二项式系数是 ______,第 4 项系数是_______。
2、写出
7)( ba ? 的展开式。
3、
6)32( ba ? 展开式的第三项为 ________________________ 。
4、
n
nnn CCC ??? ...
21
的值为( )
A、 12 ?n B 、 n2 C 、 12 ?n D、 12 ?n
5、写出
n
x
x )
2
1(
3
3 ? 展开式的第 r+1 项。
认真思考
独立作答
订正答案
总结得失
诊
断
反
思
课堂小结:
一个定理: )()( *110 NnbCbaCbaCaCba nnn
kknk
n
n
n
n
n
n ???????? ?? ??
两种思想:1.从特殊到一般的思维方式.
2.用计数原理分析二项式的展开过程.
三个注意:
1)注意二项式定理中二项展开式的特征
2)区别二项式系数,项的系数
3)掌握用通项公式求二项式系数,项的系数及项
要求:
1、静心思考,查缺补漏,找出在基础、能力方面的漏洞。
2、不讨论,独立思考,将错题重新做一遍。
提炼观点
总结归纳
作
业
布
置
1、P36 习题 1、 2、3、4 题
2、选做 (1+2x)n的展开式中第六项与第七项的系数相等,求展开式中二项式系数最大的项和
系数最大的项.
3、(课外延伸)已知在(
3
x-
1
2
3
x
)
n
的展开式中,第 6项为常数项.
(1)求 n;
(2)求含 x2的项的系数;
(3)求展开式中所有的有理项.
认真思考
独立完成
高考
链接
1.(2017.湖南高考)
1053 被 8 整除余数为( )
A、1 B 、2 C 、 3 D、7
2. ( 2018.贵阳模拟)二项式
n
4 x
1x2 ?
?
?
?
?
? ? (n?N)的展开式中,前三项的系数依次成等
差数列,则此展开式有理项的项是________________________ 。
3. (金太阳示范卷) 已知(
1 2
4
x? )n的展开式中前三项的二项式系数的和等于 37,求展式中
二项式系数最大的项的系数.
自主交流
合作探究
教导
处审
阅
教研组长审批
教学
后记
