沪科版八年级数学上册第15章轴对称图形和等腰三角形复习题(无答案)
文档属性
| 名称 | 沪科版八年级数学上册第15章轴对称图形和等腰三角形复习题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 383.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 14:32:14 | ||
图片预览


文档简介
第15章 轴对称图形与等腰三角形复习题
知识点一、 轴对称性质的应用
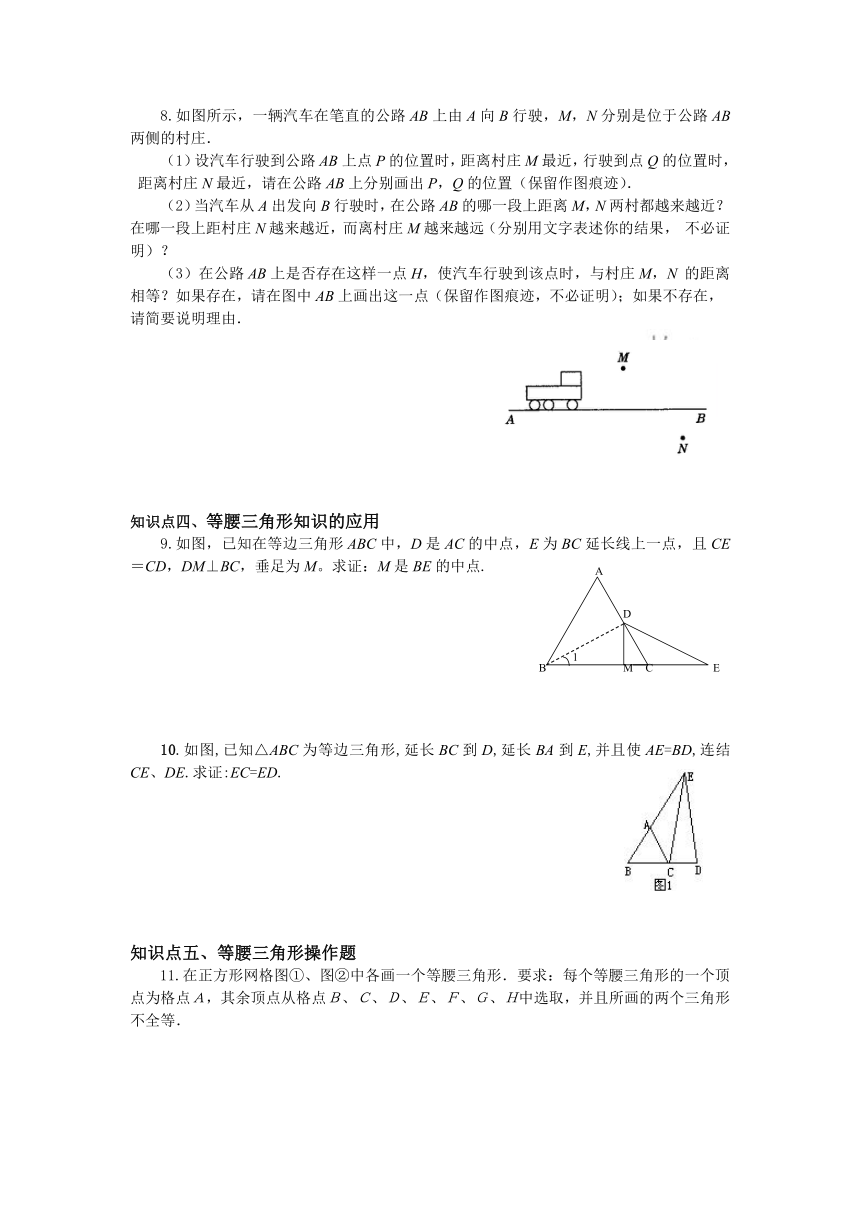
1.如图,直线l是一条河,P、Q两地相距8千米,P、Q两地到l的距离分别为2千米,5千米,欲在l上的某点M处修建一个水泵站,向P、Q两地供水.现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( )
2.已知,如图(1),Rt△ABC ≌Rt△ADE,∠ABC =∠ADE =90°.试以图中标有字母的点为端点,连结出新的线段,并请你把满足相等、或垂直、或平行关系的线段找出来,然后选择一种关系予以证明.
知识点二、线段垂直平分线知识的应用
3.如图,△ABC中,D为BC的中点,E、F分别是AB、AC上的点,且DE⊥DF,
求证:BE+CF>EF.
4.△ABC中,∠A=90°,AB=AC,D、E、F分别在AB,AC,BC上,且AD=AE,CD为EF的中垂线,求证BF=2AD.
5.已知,如图所示,DE⊥AB,DF⊥AC,垂足分别为E,F,DE=DF.求证:AD垂直平分EF.
合作学习小组的两位同学在证明以上结论时的过程如下:
学生甲:因为DE=DF,所以点D在线段EF的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),所以AD垂直平分EF.
学生乙:因为DE⊥AB,DF⊥AC,所以在Rt△ADE和Rt△ADF中,DE=DF,AD=AD,所以Rt△ADE≌Rt△ADF(HL),所以AE=AF(全等三角形的对应边相等),所以A点在线段EF的垂直平分线上,又因为DE=DF,所以点D在线段EF的垂直平分线上,所以AD垂直平分EF.
分析两位同学的证明过程,指出谁对谁错,并说明错误的原因.
知识点三、 线段垂直平分线知识的作图题
6.如图,A、B、C三点表示三个镇的地理位置,随着乡镇工业的发展需要,现三镇联合建造一所变电站,要求变电站到三镇的距离相等,请你作出变电站的位置(用P点表示),并说明你的理由.
7.A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有?请用尺规作图找出该点,保留作图痕迹,不求该点坐标.
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,并求出它的坐标.
8.如图所示,一辆汽车在笔直的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄.
(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近,行驶到点Q的位置时,距离村庄N最近,请在公路AB上分别画出P,Q的位置(保留作图痕迹).
(2)当汽车从A出发向B行驶时,在公路AB的哪一段上距离M,N两村都越来越近?在哪一段上距村庄N越来越近,而离村庄M越来越远(分别用文字表述你的结果,不必证明)?
(3)在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在,请在图中AB上画出这一点(保留作图痕迹,不必证明);如果不存在,请简要说明理由.
知识点四、等腰三角形知识的应用
9.如图,已知在等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM⊥BC,垂足为M。求证:M是BE的中点.
10.如图,已知△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连结CE、DE.求证:EC=ED.
知识点五、等腰三角形操作题
11.在正方形网格图①、图②中各画一个等腰三角形.要求:每个等腰三角形的一个顶点为格点A,其余顶点从格点B、C、D、E、F、G、H中选取,并且所画的两个三角形不全等.
12.东风汽车公司冲压汽车零件的废料都是等腰三角形的小钢板,如图1,其中AB=AC,该冲压厂为了降低汽车零件的成本,变废为宝,把这些废料加工成红星农业机械厂粉碎机上的零件,销售给红星农业机械厂,这些零件的形状都是矩形。
现在要把如图1所示的等腰三角形钢板切割后再焊接成两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每次切割次数最多两次(切割的损失忽略不计)。
(1)请你设计两种不同的切割焊接方案,并用简要的文字加以说明;
(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次),则该三角形应满足什么条件?
知识点六、 等腰三角形探究题
13.下面是数学课堂上的一个学习片断,阅读后,请回答下面的问题:
学习等腰三角形后,庞老师请同学们讨论这样一个问题上:“已知等腰三角形的两边长分别是7㎝,8㎝,请你求出三角形的周长.”
同学们经片刻思考交流后,李刚同学举手说“三角形的周长为22㎝”;王明同学说:“是23㎝”,还有一些同学也提出了不同的看法.......
(1)假如你也在课堂上,你的意见如何?为什么?
(2)通过上面数学问题的讨论,你有什么感受?(用一句话表示)
14.已知△ABC为等边三角形,在图①中,点M是线段BC上任意一点,点N线段CA上任意一点,且BM=CN,直线BN与AM相交于Q点.
(1)请猜一猜:图①中∠BQM等于多少度?
(2)若M、N两点分别在线段BC、CA的延长线上,其它条件不变,如图②所示,(1)中的结论是否仍然成立?如果成立,请加以证明;如不成立,请说明理由.
知识点七、角平分线知识的应用
15.如图,BD是∠ABC的角平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=36cm2,AB=18cm,BC=12cm,求DE的长.
16.已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC-AB=2BE.
知识点八、作图与实际问题
17.如图,点B、C在∠SAT的两边上,且AB=AC.
(1)请按下列语句用尺规画出图形(不写画法,保留作图痕迹)
①AN⊥BC,垂足为N;
②∠SBC的平分线交AN延长线于M;
③连接CM.
(2)该图中有__________对全等三角形.
18.夏令营组织学员到某一景区游玩,老师交给同学一张画有直角坐标系和标有A、B、C、D四个景点位置的地图,指出:今天我们游玩的景点E是新开发的,地图上还没来得及标注,但已知这个景点E满足:①与景点A、C和景点B、D所在的两条直线等距离;②到B、C两景点等距离.请你在平面直角坐标系中,画出景点E的位置,并标明坐标(用整数表示).
知识点九、 角平分线中的探究题
19.已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示。
20.如图,△ABC中,∠ABC与∠ACB的平分线交于点I,过I作DE∥BC交BA于D,交AC于E.
(1)你能发现哪些结论?把它们一一列出来,并选择一个加以证明.
(2)若AB=7,AC=5,你能求△ADE的周长吗?
(3)作∠ABC与∠ACB的外角平分线,他们相交于点O,过O点作BC的平行线分别交AB、AC的延长线于F、G,你还能发现什么结论?
B
A.
D
C
C
A
B
D
F
E
(1)
M
·A
·B
·C
图①
图②
A
B
S
C
T
图2
图1
知识点一、 轴对称性质的应用
1.如图,直线l是一条河,P、Q两地相距8千米,P、Q两地到l的距离分别为2千米,5千米,欲在l上的某点M处修建一个水泵站,向P、Q两地供水.现有如下四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是( )
2.已知,如图(1),Rt△ABC ≌Rt△ADE,∠ABC =∠ADE =90°.试以图中标有字母的点为端点,连结出新的线段,并请你把满足相等、或垂直、或平行关系的线段找出来,然后选择一种关系予以证明.
知识点二、线段垂直平分线知识的应用
3.如图,△ABC中,D为BC的中点,E、F分别是AB、AC上的点,且DE⊥DF,
求证:BE+CF>EF.
4.△ABC中,∠A=90°,AB=AC,D、E、F分别在AB,AC,BC上,且AD=AE,CD为EF的中垂线,求证BF=2AD.
5.已知,如图所示,DE⊥AB,DF⊥AC,垂足分别为E,F,DE=DF.求证:AD垂直平分EF.
合作学习小组的两位同学在证明以上结论时的过程如下:
学生甲:因为DE=DF,所以点D在线段EF的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上),所以AD垂直平分EF.
学生乙:因为DE⊥AB,DF⊥AC,所以在Rt△ADE和Rt△ADF中,DE=DF,AD=AD,所以Rt△ADE≌Rt△ADF(HL),所以AE=AF(全等三角形的对应边相等),所以A点在线段EF的垂直平分线上,又因为DE=DF,所以点D在线段EF的垂直平分线上,所以AD垂直平分EF.
分析两位同学的证明过程,指出谁对谁错,并说明错误的原因.
知识点三、 线段垂直平分线知识的作图题
6.如图,A、B、C三点表示三个镇的地理位置,随着乡镇工业的发展需要,现三镇联合建造一所变电站,要求变电站到三镇的距离相等,请你作出变电站的位置(用P点表示),并说明你的理由.
7.A、B两所学校在一条东西走向公路的同旁,以公路所在直线为x轴建立如图所示的平面直角坐标系,且点A的坐标是(2,2),点B的坐标是(7,3).
(1)一辆汽车由西向东行驶,在行驶过程中是否存在一点C,使C点到A、B两校的距离相等,如果有?请用尺规作图找出该点,保留作图痕迹,不求该点坐标.
(2)若在公路边建一游乐场P,使游乐场到两校距离之和最小,通过作图在图中找出建游乐场P的位置,并求出它的坐标.
8.如图所示,一辆汽车在笔直的公路AB上由A向B行驶,M,N分别是位于公路AB两侧的村庄.
(1)设汽车行驶到公路AB上点P的位置时,距离村庄M最近,行驶到点Q的位置时,距离村庄N最近,请在公路AB上分别画出P,Q的位置(保留作图痕迹).
(2)当汽车从A出发向B行驶时,在公路AB的哪一段上距离M,N两村都越来越近?在哪一段上距村庄N越来越近,而离村庄M越来越远(分别用文字表述你的结果,不必证明)?
(3)在公路AB上是否存在这样一点H,使汽车行驶到该点时,与村庄M,N的距离相等?如果存在,请在图中AB上画出这一点(保留作图痕迹,不必证明);如果不存在,请简要说明理由.
知识点四、等腰三角形知识的应用
9.如图,已知在等边三角形ABC中,D是AC的中点,E为BC延长线上一点,且CE=CD,DM⊥BC,垂足为M。求证:M是BE的中点.
10.如图,已知△ABC为等边三角形,延长BC到D,延长BA到E,并且使AE=BD,连结CE、DE.求证:EC=ED.
知识点五、等腰三角形操作题
11.在正方形网格图①、图②中各画一个等腰三角形.要求:每个等腰三角形的一个顶点为格点A,其余顶点从格点B、C、D、E、F、G、H中选取,并且所画的两个三角形不全等.
12.东风汽车公司冲压汽车零件的废料都是等腰三角形的小钢板,如图1,其中AB=AC,该冲压厂为了降低汽车零件的成本,变废为宝,把这些废料加工成红星农业机械厂粉碎机上的零件,销售给红星农业机械厂,这些零件的形状都是矩形。
现在要把如图1所示的等腰三角形钢板切割后再焊接成两种不同规格的矩形,每种矩形的面积正好等于该三角形的面积,每次切割次数最多两次(切割的损失忽略不计)。
(1)请你设计两种不同的切割焊接方案,并用简要的文字加以说明;
(2)若要把该三角形废料切割后焊接成正方形零件(只切割一次),则该三角形应满足什么条件?
知识点六、 等腰三角形探究题
13.下面是数学课堂上的一个学习片断,阅读后,请回答下面的问题:
学习等腰三角形后,庞老师请同学们讨论这样一个问题上:“已知等腰三角形的两边长分别是7㎝,8㎝,请你求出三角形的周长.”
同学们经片刻思考交流后,李刚同学举手说“三角形的周长为22㎝”;王明同学说:“是23㎝”,还有一些同学也提出了不同的看法.......
(1)假如你也在课堂上,你的意见如何?为什么?
(2)通过上面数学问题的讨论,你有什么感受?(用一句话表示)
14.已知△ABC为等边三角形,在图①中,点M是线段BC上任意一点,点N线段CA上任意一点,且BM=CN,直线BN与AM相交于Q点.
(1)请猜一猜:图①中∠BQM等于多少度?
(2)若M、N两点分别在线段BC、CA的延长线上,其它条件不变,如图②所示,(1)中的结论是否仍然成立?如果成立,请加以证明;如不成立,请说明理由.
知识点七、角平分线知识的应用
15.如图,BD是∠ABC的角平分线,DE⊥AB于点E,DF⊥BC于点F,S△ABC=36cm2,AB=18cm,BC=12cm,求DE的长.
16.已知:如图,在△ABC中,∠ABC=3∠C,∠1=∠2,BE⊥AE.
求证:AC-AB=2BE.
知识点八、作图与实际问题
17.如图,点B、C在∠SAT的两边上,且AB=AC.
(1)请按下列语句用尺规画出图形(不写画法,保留作图痕迹)
①AN⊥BC,垂足为N;
②∠SBC的平分线交AN延长线于M;
③连接CM.
(2)该图中有__________对全等三角形.
18.夏令营组织学员到某一景区游玩,老师交给同学一张画有直角坐标系和标有A、B、C、D四个景点位置的地图,指出:今天我们游玩的景点E是新开发的,地图上还没来得及标注,但已知这个景点E满足:①与景点A、C和景点B、D所在的两条直线等距离;②到B、C两景点等距离.请你在平面直角坐标系中,画出景点E的位置,并标明坐标(用整数表示).
知识点九、 角平分线中的探究题
19.已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示。
20.如图,△ABC中,∠ABC与∠ACB的平分线交于点I,过I作DE∥BC交BA于D,交AC于E.
(1)你能发现哪些结论?把它们一一列出来,并选择一个加以证明.
(2)若AB=7,AC=5,你能求△ADE的周长吗?
(3)作∠ABC与∠ACB的外角平分线,他们相交于点O,过O点作BC的平行线分别交AB、AC的延长线于F、G,你还能发现什么结论?
B
A.
D
C
C
A
B
D
F
E
(1)
M
·A
·B
·C
图①
图②
A
B
S
C
T
图2
图1
