11.4 无理数与实数 课件(2课时,34张PPT)
文档属性
| 名称 | 11.4 无理数与实数 课件(2课时,34张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 596.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 00:00:00 | ||
图片预览










文档简介
课件34张PPT。11.4 无理数与实数第一课时1.理解并掌握无理数的概念.
2.能利用概念辨别无理数.学习目标:献身科学,执着追求有两个边长为1的小正方形,通过剪、拼,设法得到一个大正方形.剪一剪 拼一拼剪一剪,拼一拼还有别的拼法吗?拼出的正方形的面积是多少?
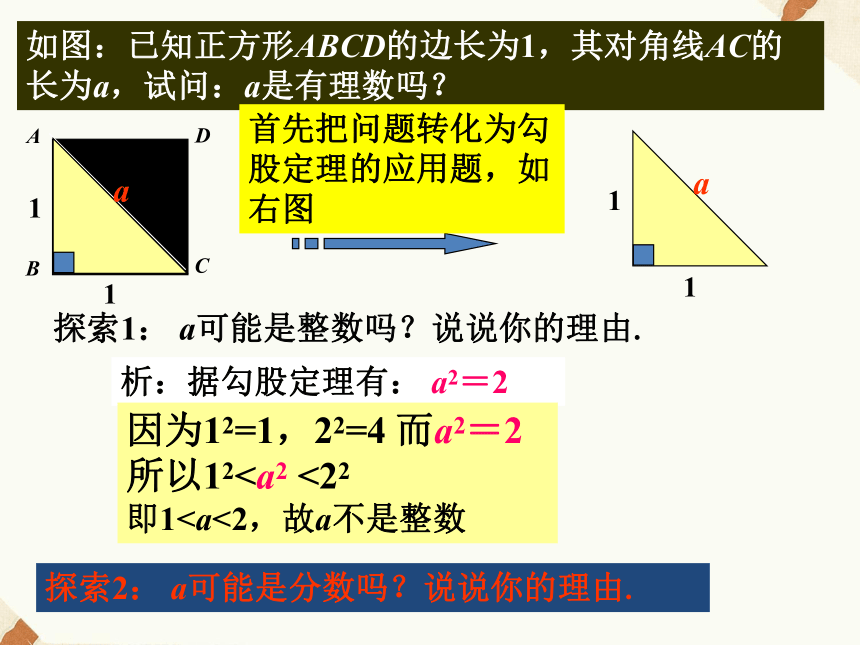
边长又是多少呢?如图:已知正方形ABCD的边长为1,其对角线AC的长为a,试问:a是有理数吗?首先把问题转化为勾股定理的应用题,如右图析:据勾股定理有: a2=2 探索1: a可能是整数吗?说说你的理由.因为12=1,22=4 而a2=2
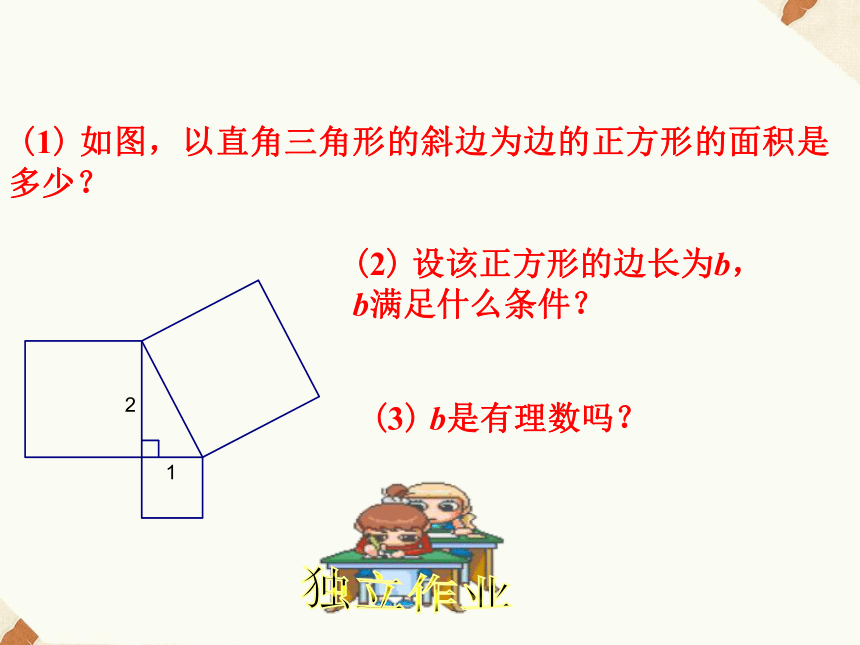
所以12即1在这个题中,两条直角边分别为1和2,斜边为b,根据勾股定理得b2=12+22,即b2=5,则b是有理数吗?因为22=4,32=9,4<5<9,所以b不可能是整数.没有两个相同的分数相乘得5,故b不可能是分数.因为没有一个整数或分数的平方为5,所以5不是有理数.1、如图,正三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?解:由正三角形的性质可知BD=1,在Rt△ABD中,由勾股定理得h2=3.h不可能是整数,也不可能是分数.一、想一想1.有理数如何分类?有理数整数(如-1,0,2,3,… ):都可看成有限小数. 2.上节课了解到一些数,如a2=2,b2=5中的a,b 既不
是整数,也不是分数,那么它们究竟是什么数呢?
二、活动与探究活动1:面积为2,5的正方形的边长a,b究竟是多少呢?练习:下列各数中,哪些是有理数?哪些是无理数?解:有理数有:无理数有:1、下面各正方形的边长不是有理数的是( )
A.面积为25的正方形
B.面积为16的正方形
C.面积为7的正方形
D.面积为1.44的正方形C设计面积为5π的圆的半径为a.
(1)a是有理数吗?说说你的理由.
(2)估计a的值(精确到十分位,并利用你的计算器验证你的估计.
(3)如果精确到百分位呢?解:∵πa2=5π,∴ a2=5 .
(1)a不是有理数,因为a既不是整数,也不是分数,而是无限不循环小数.(2)估计a≈2.2.(3)估计a≈2.24.本课小结:1.无理数的定义.2.数的分类.3.判定一个数是无理数还是有理数.第二课时 有理数集合 无理数集合 有理数集合 无理数集合有理数和无理数统称为实数,定义:即实数可以分为有理数和无理数. 正数集合 负数集合 正数集合 负数集合思考实数还可以怎样进行分类呢?实数可以分为正实数、0、负实数实数实数有理数无理数正有理数负有理数 0正无理数负无理数正实数 0负实数正有理数正无理数负有理数负无理数你学会了吗?(1)如下图,OA=OB,数轴上A点对应的数是什么?
它介于哪两个整数之间?(2)如果将所有有理数都标到数轴上,那么数轴被
填满了吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数.即实数和数轴上的点是一一对应的.你能求出下列各数的相反数、倒数和绝对值吗?想一想2;0;;在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.例1 (1)求实数 的相反数和绝对值;解:(2)求绝对值为 的实数;(3)比较无理数 和-π的大小.(1)∵ = <0.∴ 的相反数是 , (2)∵∴绝对值为 的实数实 .(3)用计算器算得 例2 比较下列各组数的大小:解: 例3 计算: .(精确到0.01)分析:≈4.899+7.937=12.836≈12.84要精确到0.01位,则我们在计算过程中要精确到0.001位,即计算的中间结果的精确度应比要求的精确度多取一位.解:一、判断:1.实数不是有理数就是无理数.( )2.无理数都是无限不循环小数.( )3.无理数都是无限小数.( )4.带根号的数都是无理数.( )5.无理数一定都带根号.( )6.两个无理数之积不一定是无理数.( )7.两个无理数之和一定是无理数.( )8.数轴上的任何一点都可以表示实数.( )×××知识小结 通过今天的学习,
用你自己的话说说你的收获和体会?
2.能利用概念辨别无理数.学习目标:献身科学,执着追求有两个边长为1的小正方形,通过剪、拼,设法得到一个大正方形.剪一剪 拼一拼剪一剪,拼一拼还有别的拼法吗?拼出的正方形的面积是多少?
边长又是多少呢?如图:已知正方形ABCD的边长为1,其对角线AC的长为a,试问:a是有理数吗?首先把问题转化为勾股定理的应用题,如右图析:据勾股定理有: a2=2 探索1: a可能是整数吗?说说你的理由.因为12=1,22=4 而a2=2
所以12
是整数,也不是分数,那么它们究竟是什么数呢?
二、活动与探究活动1:面积为2,5的正方形的边长a,b究竟是多少呢?练习:下列各数中,哪些是有理数?哪些是无理数?解:有理数有:无理数有:1、下面各正方形的边长不是有理数的是( )
A.面积为25的正方形
B.面积为16的正方形
C.面积为7的正方形
D.面积为1.44的正方形C设计面积为5π的圆的半径为a.
(1)a是有理数吗?说说你的理由.
(2)估计a的值(精确到十分位,并利用你的计算器验证你的估计.
(3)如果精确到百分位呢?解:∵πa2=5π,∴ a2=5 .
(1)a不是有理数,因为a既不是整数,也不是分数,而是无限不循环小数.(2)估计a≈2.2.(3)估计a≈2.24.本课小结:1.无理数的定义.2.数的分类.3.判定一个数是无理数还是有理数.第二课时 有理数集合 无理数集合 有理数集合 无理数集合有理数和无理数统称为实数,定义:即实数可以分为有理数和无理数. 正数集合 负数集合 正数集合 负数集合思考实数还可以怎样进行分类呢?实数可以分为正实数、0、负实数实数实数有理数无理数正有理数负有理数 0正无理数负无理数正实数 0负实数正有理数正无理数负有理数负无理数你学会了吗?(1)如下图,OA=OB,数轴上A点对应的数是什么?
它介于哪两个整数之间?(2)如果将所有有理数都标到数轴上,那么数轴被
填满了吗?BA每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一点都表示一个实数.即实数和数轴上的点是一一对应的.你能求出下列各数的相反数、倒数和绝对值吗?想一想2;0;;在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样.例1 (1)求实数 的相反数和绝对值;解:(2)求绝对值为 的实数;(3)比较无理数 和-π的大小.(1)∵ = <0.∴ 的相反数是 , (2)∵∴绝对值为 的实数实 .(3)用计算器算得 例2 比较下列各组数的大小:解: 例3 计算: .(精确到0.01)分析:≈4.899+7.937=12.836≈12.84要精确到0.01位,则我们在计算过程中要精确到0.001位,即计算的中间结果的精确度应比要求的精确度多取一位.解:一、判断:1.实数不是有理数就是无理数.( )2.无理数都是无限不循环小数.( )3.无理数都是无限小数.( )4.带根号的数都是无理数.( )5.无理数一定都带根号.( )6.两个无理数之积不一定是无理数.( )7.两个无理数之和一定是无理数.( )8.数轴上的任何一点都可以表示实数.( )×××知识小结 通过今天的学习,
用你自己的话说说你的收获和体会?
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
