12.2 三角形的性质 课件（20张PPT）
文档属性
| 名称 | 12.2 三角形的性质 课件（20张PPT） |
|
|
| 格式 | zip | ||
| 文件大小 | 243.7KB | ||
| 资源类型 | 课件 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 00:00:00 | ||
文档简介
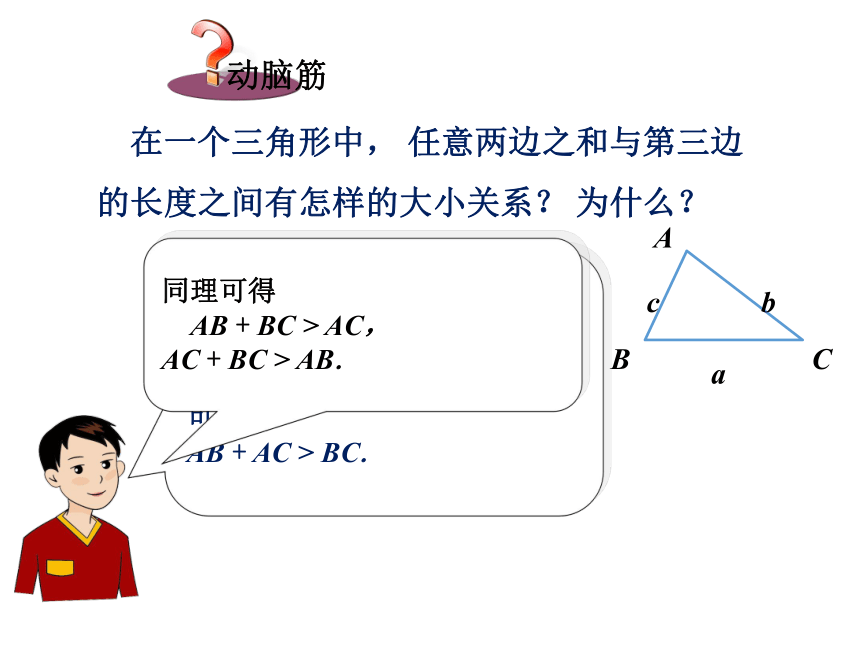
课件20张PPT。12.2 三角形的性质 在一个三角形中， 任意两边之和与第三边的长度之间有怎样的大小关系？ 为什么？如图， 在△ABC中， BC是连接B， C两点的一条线段， 由基本事实“两点之间线段最短” 可得
AB + AC > BC.
同理可得
AB + BC > AC，
AC + BC > AB.
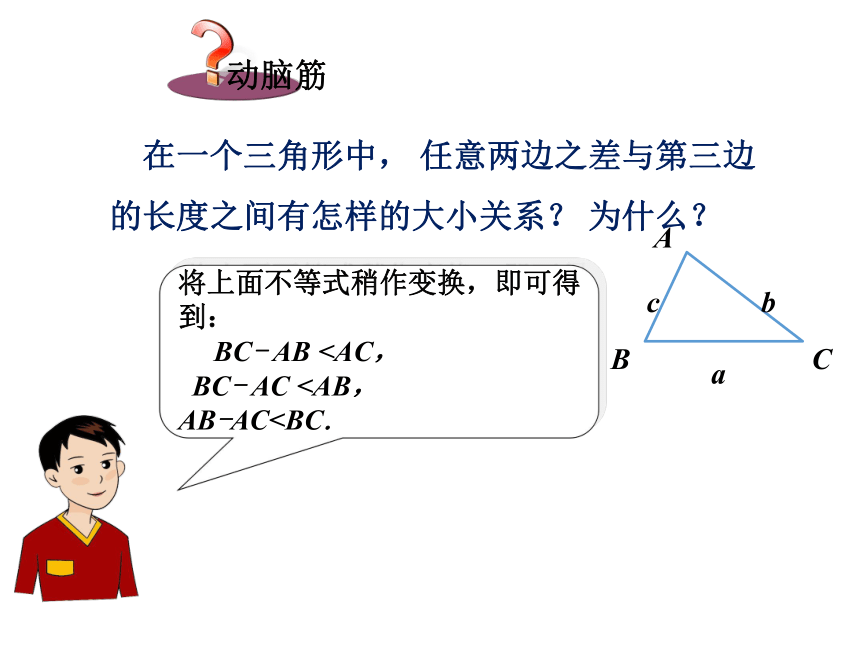
ABCabc 在一个三角形中， 任意两边之差与第三边的长度之间有怎样的大小关系？ 为什么？
将上面不等式稍作变换，即可得到：
BC- AB BC- AC AB-ACABCabc三角形的任意两边之和大于第三边.三角形的任意两边之差小于第三边.例1 等腰三角形中周长为18cm
1、如果腰长是底边长的2倍，求各边的长；
2、如果一边长为4cm，求另两边的长. (1)设等腰三角形的底边长为xcm，
则腰长为2xcm，根据题意，得x+2x+2x=18解方程，得x=3.6解：例题解析(2)若底边长为4cm，设腰长为xcm，则有2x+4=18解方程，得x=7若一条腰长为4cm，设底边长为xcm，则有2×4+x=18x=10解方程，得因为4+4<10，所以4cm为一腰不能构成三角形所以，三角形的另两边长都是7cm例题解析我们知道三角形三个内角的和等于180°.
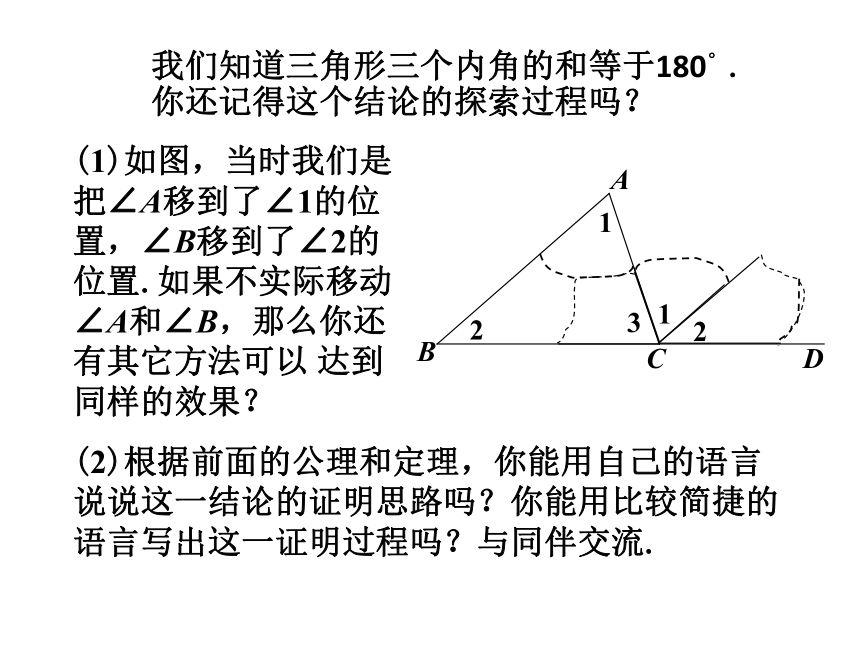
你还记得这个结论的探索过程吗？12ABD3C(1)如图，当时我们是把∠A移到了∠1的位置，∠B移到了∠2的位置.如果不实际移动∠A和∠B，那么你还有其它方法可以 达到同样的效果？(2)根据前面的公理和定理，你能用自己的语言说说这一结论的证明思路吗？你能用比较简捷的语言写出这一证明过程吗？与同伴交流.已知:如图△ABC.
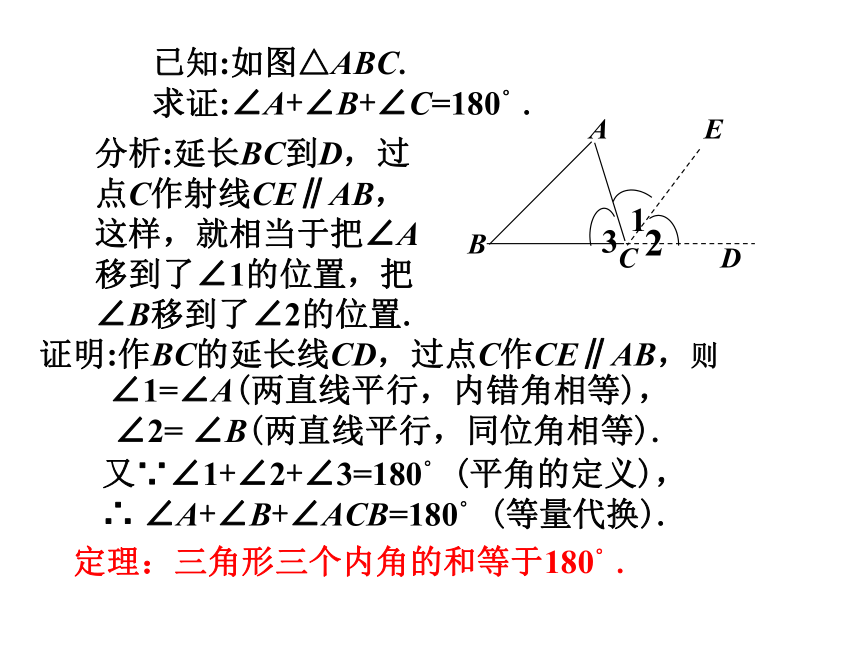
求证:∠A+∠B+∠C=180°.证明:作BC的延长线CD，过点C作CE∥AB，则定理：三角形三个内角的和等于180°. ∠1=∠A(两直线平行，内错角相等)， ∠2= ∠B(两直线平行，同位角相等). 又∵∠1+∠2+∠3=180° (平角的定义)， ∴ ∠A+∠B+∠ACB=180° (等量代换).分析:延长BC到D，过点C作射线CE∥AB，这样，就相当于把∠A移到了∠1的位置，把∠B移到了∠2的位置.例2 已知：如图，在△ABC中，∠A=100°， ∠B=∠C.
求： ∠B，∠C的度数.解：设∠B的度数为x.
∵ ∠B=∠C，
∴∠C的度数也为x.
∵∠A+ ∠B+∠C=180°，
∴100+x+x=180，
2x=80.
∴x=40.
即∠B=40°，∠C=40°.看一看图中有几个小于 180o的角？这些角从位置
上看有什么不一样吗？B21ACD概念学习B21ACD三角形的一边与另一边的延长线组成的角，
叫做三角形的外角.如∠ACD. ∠A＋∠B ＋∠1 ＝ ∠ACD＋∠1 ＝180o180o 思考：1 、一个三角形有多少个外角？2、请根据图形填空.(三角形内角和定理) ∠ACD ＝ ∠A＋∠B结论：三角形的一个外角等于与它不相邻的两个内角的和.想一想 说一说你能根据上面两个等式得到什么样的式子，能用自己的语言表达吗？ ∠ACD ∠A (<、>)；∠ACD ∠B (<、>)结论：三角形的一个外角大于任何一个与它不相邻的内角.D>>你选谁 ？ 例3 如图，∠BAE，∠CBF，∠ACD 是△ABC 的
三个外角，它们的和是多少？∵ ∠BAE =∠2 +∠3，
∠CBF =∠1 +∠3，
∠ACD =∠1 +∠2，
∴ ∠BAE +∠CBF +∠ACD
= (∠2 +∠3)+(∠1 +∠3)
+ (∠1 +∠2)
= 2(∠1 +∠2 +∠3)= 2×180°=360°例题解析1.三个角的内角中最多能有几个直角？
2.三角形的内角中最多能有几个钝角？思考与交流三个角都是锐角的三角形叫做锐角三角形；
有一个角是直角的三角形叫做直角三角形；
有一个角是钝角的三角形叫做钝角三角形.按角分锐角三角形直角三角形钝角三角形斜三角形直角三角形的一个判定方法：有两个锐角互余的三角形是直角三角形.练一练1、求下列各图中∠1的度数.∠1=∠1=∠1=判断题：1、三角形的外角和是指三角形所有外角的和.( )
2、三角形的外角和等于它内角和的2倍.( )
3、三角形的一个外角等于两个内角的和.( )
4、三角形的一个外角等于与它不相邻的两个内角的和.( )
5、三角形的一个外角大于任何一个内角.( )
1.三角形的基本性质3.三角形三边之角的关系2.三角形三边之间的关系课堂小结
AB + AC > BC.
同理可得
AB + BC > AC，
AC + BC > AB.
ABCabc 在一个三角形中， 任意两边之差与第三边的长度之间有怎样的大小关系？ 为什么？
将上面不等式稍作变换，即可得到：
BC- AB
1、如果腰长是底边长的2倍，求各边的长；
2、如果一边长为4cm，求另两边的长. (1)设等腰三角形的底边长为xcm，
则腰长为2xcm，根据题意，得x+2x+2x=18解方程，得x=3.6解：例题解析(2)若底边长为4cm，设腰长为xcm，则有2x+4=18解方程，得x=7若一条腰长为4cm，设底边长为xcm，则有2×4+x=18x=10解方程，得因为4+4<10，所以4cm为一腰不能构成三角形所以，三角形的另两边长都是7cm例题解析我们知道三角形三个内角的和等于180°.
你还记得这个结论的探索过程吗？12ABD3C(1)如图，当时我们是把∠A移到了∠1的位置，∠B移到了∠2的位置.如果不实际移动∠A和∠B，那么你还有其它方法可以 达到同样的效果？(2)根据前面的公理和定理，你能用自己的语言说说这一结论的证明思路吗？你能用比较简捷的语言写出这一证明过程吗？与同伴交流.已知:如图△ABC.
求证:∠A+∠B+∠C=180°.证明:作BC的延长线CD，过点C作CE∥AB，则定理：三角形三个内角的和等于180°. ∠1=∠A(两直线平行，内错角相等)， ∠2= ∠B(两直线平行，同位角相等). 又∵∠1+∠2+∠3=180° (平角的定义)， ∴ ∠A+∠B+∠ACB=180° (等量代换).分析:延长BC到D，过点C作射线CE∥AB，这样，就相当于把∠A移到了∠1的位置，把∠B移到了∠2的位置.例2 已知：如图，在△ABC中，∠A=100°， ∠B=∠C.
求： ∠B，∠C的度数.解：设∠B的度数为x.
∵ ∠B=∠C，
∴∠C的度数也为x.
∵∠A+ ∠B+∠C=180°，
∴100+x+x=180，
2x=80.
∴x=40.
即∠B=40°，∠C=40°.看一看图中有几个小于 180o的角？这些角从位置
上看有什么不一样吗？B21ACD概念学习B21ACD三角形的一边与另一边的延长线组成的角，
叫做三角形的外角.如∠ACD. ∠A＋∠B ＋∠1 ＝ ∠ACD＋∠1 ＝180o180o 思考：1 、一个三角形有多少个外角？2、请根据图形填空.(三角形内角和定理) ∠ACD ＝ ∠A＋∠B结论：三角形的一个外角等于与它不相邻的两个内角的和.想一想 说一说你能根据上面两个等式得到什么样的式子，能用自己的语言表达吗？ ∠ACD ∠A (<、>)；∠ACD ∠B (<、>)结论：三角形的一个外角大于任何一个与它不相邻的内角.D>>你选谁 ？ 例3 如图，∠BAE，∠CBF，∠ACD 是△ABC 的
三个外角，它们的和是多少？∵ ∠BAE =∠2 +∠3，
∠CBF =∠1 +∠3，
∠ACD =∠1 +∠2，
∴ ∠BAE +∠CBF +∠ACD
= (∠2 +∠3)+(∠1 +∠3)
+ (∠1 +∠2)
= 2(∠1 +∠2 +∠3)= 2×180°=360°例题解析1.三个角的内角中最多能有几个直角？
2.三角形的内角中最多能有几个钝角？思考与交流三个角都是锐角的三角形叫做锐角三角形；
有一个角是直角的三角形叫做直角三角形；
有一个角是钝角的三角形叫做钝角三角形.按角分锐角三角形直角三角形钝角三角形斜三角形直角三角形的一个判定方法：有两个锐角互余的三角形是直角三角形.练一练1、求下列各图中∠1的度数.∠1=∠1=∠1=判断题：1、三角形的外角和是指三角形所有外角的和.( )
2、三角形的外角和等于它内角和的2倍.( )
3、三角形的一个外角等于两个内角的和.( )
4、三角形的一个外角等于与它不相邻的两个内角的和.( )
5、三角形的一个外角大于任何一个内角.( )
1.三角形的基本性质3.三角形三边之角的关系2.三角形三边之间的关系课堂小结
常见问题
这份课件适用于什么教材版本？
本课件适用于北京课改版相关教学场景，可在21世纪教育网检索同版本配套资源。
适用学段和科目是什么？
适用学段与科目：初中、8、数学。
文件是什么格式，大小多少？
文件格式为 ZIP，文件大小约 243.7KB。
文档主要包含哪些内容？
课件20张PPT。12.2 三角形的性质 在一个三角形中， 任意两边之和与第三边的长度之间有怎样的大小关系？ 为什么？如图， 在△ABC中， BC是连接B， C两点的一条线段， 由基本事实“两点之间线段最短” 可得AB + AC >…
如何获取完整文档？
页面提供 9 页预览图片，完整文档可通过21世纪教育网下载页 /t/6651945 获取。