12.7 直角三角形 课件(16张PPT)
文档属性
| 名称 | 12.7 直角三角形 课件(16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 15:22:02 | ||
图片预览





文档简介
课件16张PPT。12.7 直角三角形复习回顾1、什么是直角三角形?
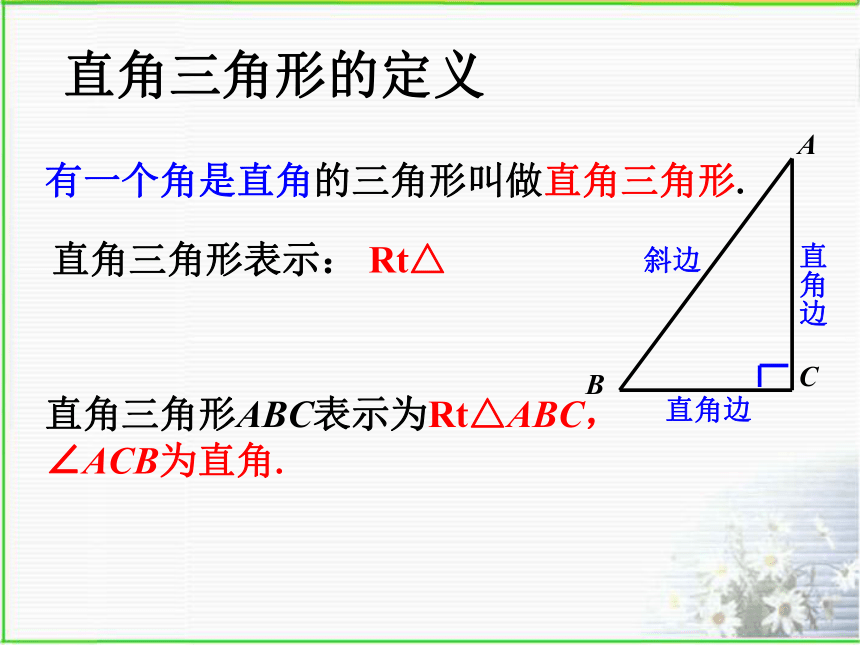
有一个内角是直角的三角形叫直角三角形.
直角三角形可表示: Rt△ABCACB斜边直角边直角边猜想:直角三角形的两个锐角有什么关系?有一个角是直角的三角形叫做直角三角形.直角三角形表示: Rt△ 直角边
斜边直角边直角三角形ABC表示为Rt△ABC,
∠ACB为直角.直角三角形的定义想一想:CB斜
边直角边直角边A1.直角三角形的内角
有什么特点?
2.直角三角形的两个
锐角之间有什么关系?猜想:直角三角形的两个锐角互余直角三角形的性质证明:在△ABC中
∵∠A+∠B+∠C=180゜(三角形内角和定理)
∠C= 90゜(已知)
∴∠A+∠B+90゜=180゜
∴∠A+∠B=180゜-90゜= 90゜
即∠A+∠B=90゜ABC已知:在△ABC中,∠C= 90゜
求证:∠A+∠B=90 ゜ 对猜想证明:结论:
直角三角形的两锐角互余直角三角形的两个锐角互余∵∠ACB=90°∴∠A+∠B=90°几何语言直角三角形的性质:想一想:CB斜
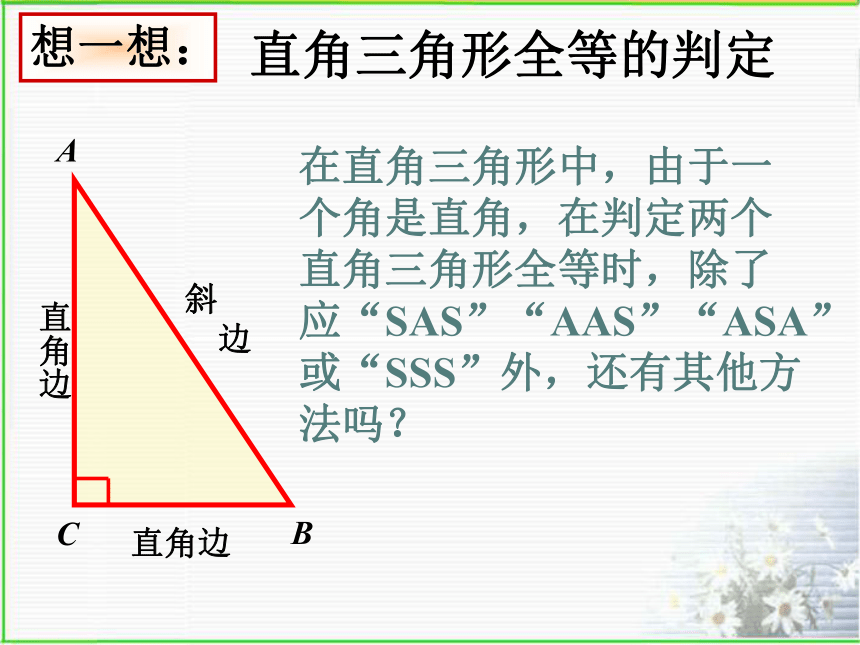
边直角边直角边A在直角三角形中,由于一个角是直角,在判定两个直角三角形全等时,除了应“SAS”“AAS”“ASA”或“SSS”外,还有其他方法吗?直角三角形全等的判定定理:如果两个直角三角形的斜边 和一条直角边分别对应相等,那么这两个直角三角形全等 .简单的用“斜边、直角边”或“HL”表示 证明示范:在Rt?ABC和Rt?DEF中AB=DEAC=DF∴ Rt?ABC ≌ Rt?DEF (HL)例 已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,且BD=CE.
求证:AB=AC.证明:在△BDC和△CEB中,
∵ BD⊥AC于D,CE⊥AB于E,
∴∠BDC和∠CEB是直角.
在Rt△BDC和Rt△CEB中,∴ Rt?BDC ≌ Rt?CEB (HL).∴ ∠CBD=∠CBE(全等三角形对应角相等).
∴AB=AC(等角对等边).1. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?解:在Rt△ACB和Rt△ADB中,∴ Rt△ACB≌Rt△ADB (HL)∴BC=BD
(全等三角形对应边相等).随堂演练练一练1、在△ABC中,∠C=90°,∠A=30°,
∠B= . 直角三角形两个锐角之差是10°,则较大 的锐角是 度.3、直角三角形的两个锐角的平分线所构成的
角是 度.60° 50° 45°或135°2、4、如图,CD是Rt△ABC斜边上的高,请找出图中各对互余的角.(1)相等的锐角有几对?(2)过D作DE⊥BC于点E ,
图中有几对互余的角.12345、如图, ∠C =∠D,请你再添加一个条件,使△ABD ≌ △BAC,并在添加的条件后的( )内写出判定全等的依据.
(1) ( )
(2) ( )
(3) ( )
(4) ( )AD=BC∠ DAB= ∠ CBABD=AC∠ DBA= ∠ CABHL HLAASAAS(1)直角三角形的两个锐角互余.小结:(2)如果两个直角三角形的斜边和一条直角边分别对应相等,那么这两个直角三角形全等 .谢谢观看!
有一个内角是直角的三角形叫直角三角形.
直角三角形可表示: Rt△ABCACB斜边直角边直角边猜想:直角三角形的两个锐角有什么关系?有一个角是直角的三角形叫做直角三角形.直角三角形表示: Rt△ 直角边
斜边直角边直角三角形ABC表示为Rt△ABC,
∠ACB为直角.直角三角形的定义想一想:CB斜
边直角边直角边A1.直角三角形的内角
有什么特点?
2.直角三角形的两个
锐角之间有什么关系?猜想:直角三角形的两个锐角互余直角三角形的性质证明:在△ABC中
∵∠A+∠B+∠C=180゜(三角形内角和定理)
∠C= 90゜(已知)
∴∠A+∠B+90゜=180゜
∴∠A+∠B=180゜-90゜= 90゜
即∠A+∠B=90゜ABC已知:在△ABC中,∠C= 90゜
求证:∠A+∠B=90 ゜ 对猜想证明:结论:
直角三角形的两锐角互余直角三角形的两个锐角互余∵∠ACB=90°∴∠A+∠B=90°几何语言直角三角形的性质:想一想:CB斜
边直角边直角边A在直角三角形中,由于一个角是直角,在判定两个直角三角形全等时,除了应“SAS”“AAS”“ASA”或“SSS”外,还有其他方法吗?直角三角形全等的判定定理:如果两个直角三角形的斜边 和一条直角边分别对应相等,那么这两个直角三角形全等 .简单的用“斜边、直角边”或“HL”表示 证明示范:在Rt?ABC和Rt?DEF中AB=DEAC=DF∴ Rt?ABC ≌ Rt?DEF (HL)例 已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,且BD=CE.
求证:AB=AC.证明:在△BDC和△CEB中,
∵ BD⊥AC于D,CE⊥AB于E,
∴∠BDC和∠CEB是直角.
在Rt△BDC和Rt△CEB中,∴ Rt?BDC ≌ Rt?CEB (HL).∴ ∠CBD=∠CBE(全等三角形对应角相等).
∴AB=AC(等角对等边).1. 如图,AC=AD,∠C,∠D是直角,将上述条件标注在图中,你能说明BC与BD相等吗?解:在Rt△ACB和Rt△ADB中,∴ Rt△ACB≌Rt△ADB (HL)∴BC=BD
(全等三角形对应边相等).随堂演练练一练1、在△ABC中,∠C=90°,∠A=30°,
∠B= . 直角三角形两个锐角之差是10°,则较大 的锐角是 度.3、直角三角形的两个锐角的平分线所构成的
角是 度.60° 50° 45°或135°2、4、如图,CD是Rt△ABC斜边上的高,请找出图中各对互余的角.(1)相等的锐角有几对?(2)过D作DE⊥BC于点E ,
图中有几对互余的角.12345、如图, ∠C =∠D,请你再添加一个条件,使△ABD ≌ △BAC,并在添加的条件后的( )内写出判定全等的依据.
(1) ( )
(2) ( )
(3) ( )
(4) ( )AD=BC∠ DAB= ∠ CBABD=AC∠ DBA= ∠ CABHL HLAASAAS(1)直角三角形的两个锐角互余.小结:(2)如果两个直角三角形的斜边和一条直角边分别对应相等,那么这两个直角三角形全等 .谢谢观看!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
