12.7 直角三角形 课件(18张PPT)
文档属性
| 名称 | 12.7 直角三角形 课件(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 344.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 15:22:02 | ||
图片预览




文档简介
课件18张PPT。12.7 直角三角形
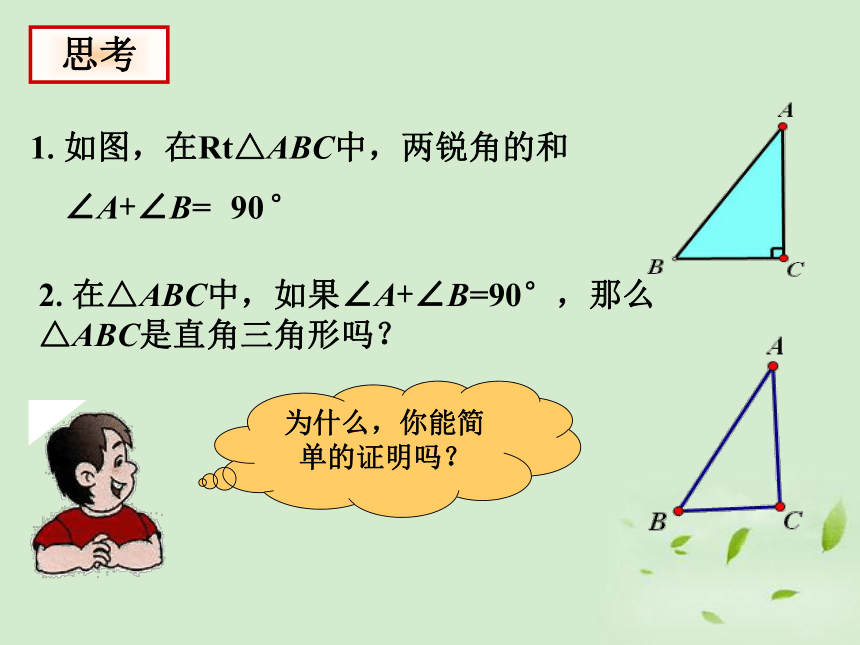
1、全等三角形的对应边 ---------,对应角-----------.相等相等2、判定三角形全等的方法有:SAS、ASA、AAS、SSS直角边直角边斜边认识直角三角形Rt△ABC亿一亿1.如图,在Rt△ABC中,两锐角的和
∠A+∠B=90 °思考证明:在△ABC中
∵∠A+∠B+∠C=180゜(三角形内角和定理)
∠C= 90゜(已知)
∴∠A+∠B+90゜=180゜
∴∠A+∠B=180゜-90゜= 90゜
即∠A+∠B=90゜ABC已知:在△ABC中,∠C= 90゜
求证:∠A+∠B=90 ゜对猜想证明:结论:
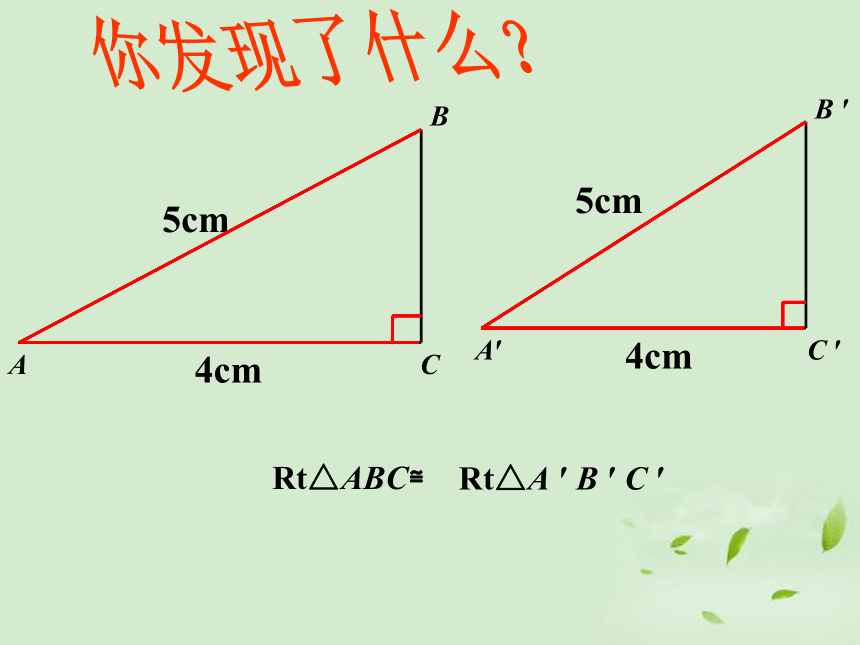
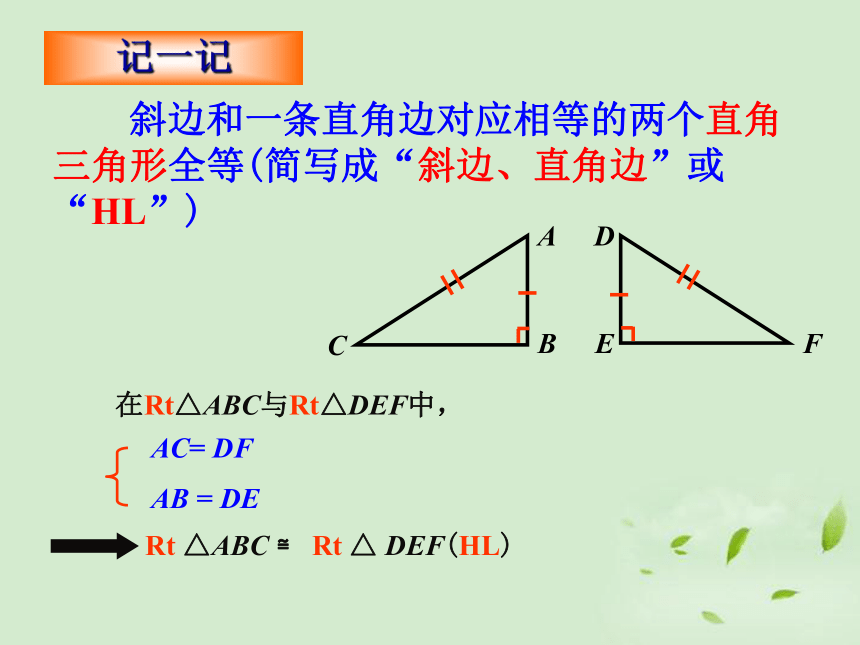
直角三角形的两锐角互余直角三角形的性质直角三角形的两个锐角角互余.你发现了什么?AB = DEAC= DFRt △ABC ≌ Rt △ DEF(HL) 斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)? 记一记 ? 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”前提条件1条件21、证题前先分析(方法是“三步走”)
2、证明线段或角相等有时需通过两次全等来实现
3、注意解题格式注意:例 已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,且BD=CE.
求证:AB=AC.例题解析证明:在△BDC和△CEB中,
∵ BD⊥AC于D,CE⊥AB于E,
∴∠BDC和∠CEB是直角.
在Rt△BDC和Rt△CEB中,∴ Rt?BDC ≌ Rt?CEB (HL).∴ ∠CBD=∠CBE(全等三角形对应角相等).
∴AB=AC(等角对等边).例题解析 1.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.随堂练习解:BD=CD;
因为∠ADB=∠ADC=90°
在Rt△ABD和Rt△ACD中,
AB=AC=12米,
AD=AD,所以Rt△ABD≌Rt△ACD (HL)
所以BD=CD随堂练习2、如图是用两根长度相等的拉线固定电线杆的示意图.其中一根拉到B,另一根拉到C.那么C、B两端点到D的距离DC和DB的大小有何关系?说明理由.BACDAD = ADAB= ACRt△ABD ≌ Rt△ADC (HL)答: OC = OB随堂练习 3.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?∠ABC+∠DFE=90°.随堂练习解:在Rt△ABC和Rt△DEF中∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.∠ABC和∠DFE的大小有什么关系?谢谢观看!
1、全等三角形的对应边 ---------,对应角-----------.相等相等2、判定三角形全等的方法有:SAS、ASA、AAS、SSS直角边直角边斜边认识直角三角形Rt△ABC亿一亿1.如图,在Rt△ABC中,两锐角的和
∠A+∠B=90 °思考证明:在△ABC中
∵∠A+∠B+∠C=180゜(三角形内角和定理)
∠C= 90゜(已知)
∴∠A+∠B+90゜=180゜
∴∠A+∠B=180゜-90゜= 90゜
即∠A+∠B=90゜ABC已知:在△ABC中,∠C= 90゜
求证:∠A+∠B=90 ゜对猜想证明:结论:
直角三角形的两锐角互余直角三角形的性质直角三角形的两个锐角角互余.你发现了什么?AB = DEAC= DFRt △ABC ≌ Rt △ DEF(HL) 斜边和一条直角边对应相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)? 记一记 ? 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等.简写成“斜边、直角边”或“HL”前提条件1条件21、证题前先分析(方法是“三步走”)
2、证明线段或角相等有时需通过两次全等来实现
3、注意解题格式注意:例 已知:如图,在△ABC中,BD⊥AC于D,CE⊥AB于E,且BD=CE.
求证:AB=AC.例题解析证明:在△BDC和△CEB中,
∵ BD⊥AC于D,CE⊥AB于E,
∴∠BDC和∠CEB是直角.
在Rt△BDC和Rt△CEB中,∴ Rt?BDC ≌ Rt?CEB (HL).∴ ∠CBD=∠CBE(全等三角形对应角相等).
∴AB=AC(等角对等边).例题解析 1.如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由.随堂练习解:BD=CD;
因为∠ADB=∠ADC=90°
在Rt△ABD和Rt△ACD中,
AB=AC=12米,
AD=AD,所以Rt△ABD≌Rt△ACD (HL)
所以BD=CD随堂练习2、如图是用两根长度相等的拉线固定电线杆的示意图.其中一根拉到B,另一根拉到C.那么C、B两端点到D的距离DC和DB的大小有何关系?说明理由.BACDAD = ADAB= ACRt△ABD ≌ Rt△ADC (HL)答: OC = OB随堂练习 3.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?∠ABC+∠DFE=90°.随堂练习解:在Rt△ABC和Rt△DEF中∴ Rt△ABC≌Rt△DEF (HL).∴∠ABC=∠DEF
(全等三角形对应角相等).∵ ∠DEF+∠DFE=90°,∴∠ABC+∠DFE=90°.∠ABC和∠DFE的大小有什么关系?谢谢观看!
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
