12.6 等腰三角形 课件(23张PPT)
文档属性
| 名称 | 12.6 等腰三角形 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 529.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 00:00:00 | ||
图片预览







文档简介
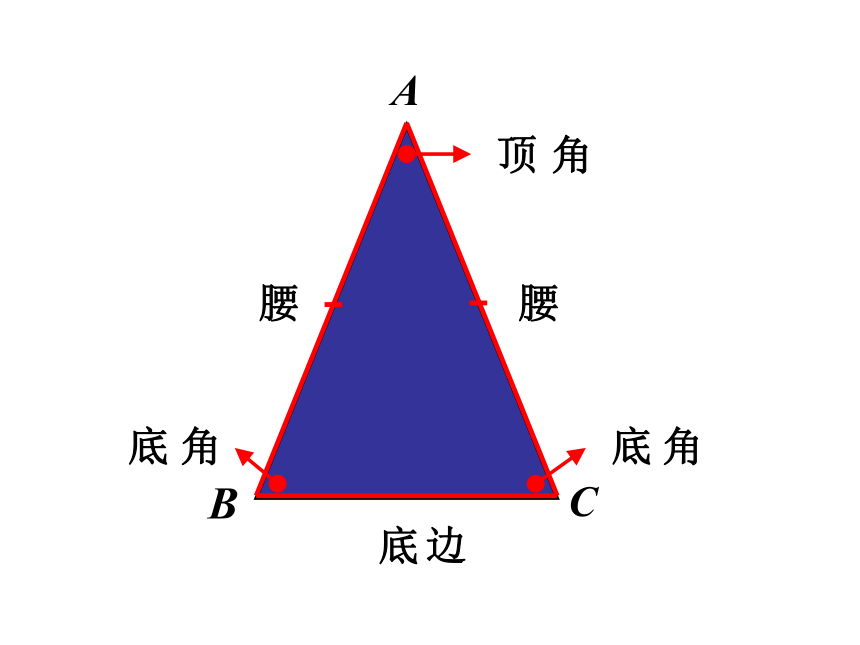
课件23张PPT。12.6 等腰三角形都有等腰三角形三条边都相等的三角形叫做等边三角形.
三条边互不相等的三角形叫做不等边三角形.三角形按边分类:三条边都相等的三角形叫做等边三角形.
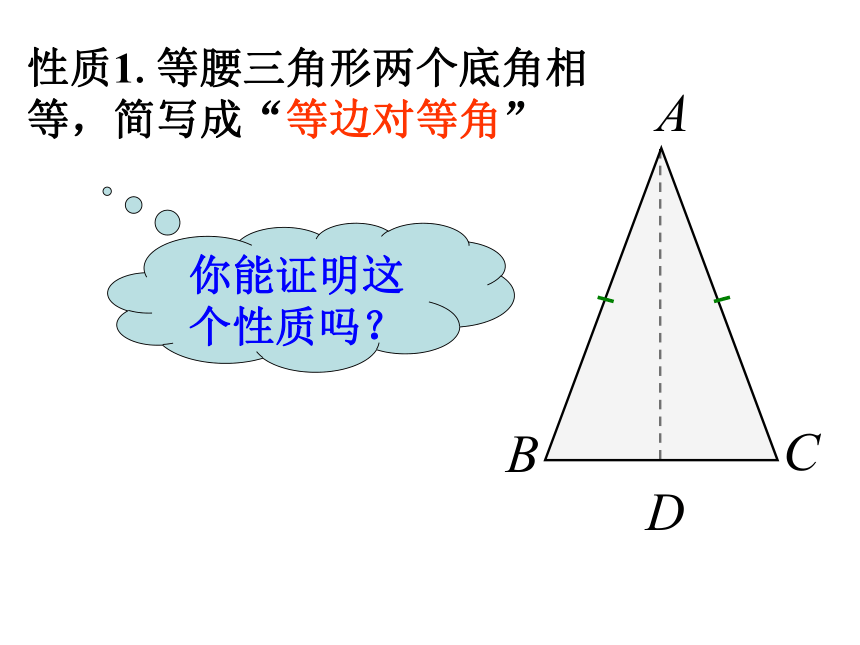
三条边互不相等的三角形叫做不等边三角形.三角形按边分类用集合表示为:等腰三角形不等边三角形性质1.等腰三角形两个底角相等,简写成“等边对等角”你能证明这个性质吗?例1、已知:在△ABC中,AB=AC,∠A=120.求∠C和∠B的度数.解:∵ AB=AC,∴ ∠C=∠B( 等边对等角)∵ ∠A+∠B +∠C=180.(三角形内角和等于180.)∠A=120 ° , ∴∠B+∠C=180 °-120 ° =60°
∴∠B=∠C=30.性质2.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.简称“三线合一”.交流观察下图能得出什么猜想?想一想:我们都知道,等边三角形是特殊的等腰三角形.根据等腰三角形的性质可得,等边三角形有什么性质?推论:等边三角形三个内角相等,每一个内角都等于60°.例2 ,已知:在△ABC中,AB=AC.小明想作∠BAC的角平分线,但他没有量角器,只有刻度尺,他如何作出∠BAC的角平分线?解:取BC得中点D,连接AD,那么AD平分∠BAC.△ABC中,因为AB=AC是底边上的中线,根据三线合一定理,AD是顶角的角平分线.∵AB=AC,AD=DC,AE=EB, ∴DC=BE,∠DCB=∠EBC. ∵BC=CB, ∴△BDC≌△CEB(SAS). ∴BD=CE.已知:AB=AC,AD=DC,AE=EB.
求证:BD=CE.证明:例3 证明:等腰三角形两腰上的中线相等.思考 :1、如图:ΔABC中,已知AB=AC∠B=∠C(在同一个三角形中,等边对等角).2、反过来:在ΔABC中,∠ B= ∠ C,AB=AC成立吗?ABC已知:ΔABC中,∠B=∠C求证:AB=AC证明:∴ ΔADB≌ ΔADC(AAS)∴AB=AC(全等三角形的对应边
相等)过A作ADBC,D为垂足,
∠ADB= ∠ADC=90 °.
在ΔADB和ΔADC中
∴∠B= ∠C
∠ADB= ∠ADCAD= AD
∴ AC=AB. ( )已知在一个三角形中,等角对等边定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形. 在△ABC中, ∵∠B=∠C ( )用符号语言表示为:这又是一个判定两条线段相等根据之一.例4 如图,∠A=72°,∠B=36°,CD平分∠ACB.试指出图中的哪些三角形是等腰三角形,并说明理由.解:△BAC,△DBC,△CAD为等腰三角形.∵∠ACB=180°-∠A-∠B
=180°-72°-36°=72°,∵CD平分∠ACB,∠ACD=∠BCD=36°,∴∠A=∠ACB=72° . ∴△BAC为等腰三角形.∴∠B=∠BCD=36°, ∴∠A=∠ADC=72° .∵△CAD为等腰三角形,∴△DBC为等腰三角形.∠ADC=180°-∠A-∠ACD
=180°-72°-36°
=72°推论1:证明已知:如图,ΔABC中, ∠ A=∠B=∠C
求证:AB=AC=BC证明:在ΔABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB推论1.三个角都相等的三角形是等边三角形推论2:证明问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?第一种情况:当顶角是60度时.
第二种情况:当底角是60度时.已知: ΔABC中,AB=AC, ∠B=60°.
求证:AB=AC=BC证明: ΔABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=60°
∴ ∠C = 60°
∴∠ A=60°
∴AB=AC=BC
有一个角是60°的等腰三角形是等边三角形.例5 如图,∠A=∠B,CE∥DA.求证:CE=CB.
需再增加什么条件,可使△BCE成为等边
三角形?证:∵CE∥DA,∴∠A=∠BEC.又∵∠A=∠B,∴∠B=∠BEC,∴△CBE为等腰三角形,∴CB=CE.要使△BCE为等边三角形,即只要满足CB=CE=BE=60°即可.则三角形的三条边应相等,1.判断下列语句是否正确.(1)等腰三角形的角平分线、中线和高互相重合.( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°. ( )
(3)等腰三角形的底角一定是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××证明:∵AE∥DC,∴∠C=∠AEB. ——①又∵AB=AE, ∴△ABE为等腰三角形,∴∠B=∠AEB. ——②由①②可得∠B=∠C.2.如图,点E在BC上,
AE∥DC,AB=AE.
求证:∠B=∠C. 有两边相等的三角形是等腰三角形2.等边对等角3. 三线合一2.等角对等边1.两边相等1.两腰相等小结
三条边互不相等的三角形叫做不等边三角形.三角形按边分类:三条边都相等的三角形叫做等边三角形.
三条边互不相等的三角形叫做不等边三角形.三角形按边分类用集合表示为:等腰三角形不等边三角形性质1.等腰三角形两个底角相等,简写成“等边对等角”你能证明这个性质吗?例1、已知:在△ABC中,AB=AC,∠A=120.求∠C和∠B的度数.解:∵ AB=AC,∴ ∠C=∠B( 等边对等角)∵ ∠A+∠B +∠C=180.(三角形内角和等于180.)∠A=120 ° , ∴∠B+∠C=180 °-120 ° =60°
∴∠B=∠C=30.性质2.等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.简称“三线合一”.交流观察下图能得出什么猜想?想一想:我们都知道,等边三角形是特殊的等腰三角形.根据等腰三角形的性质可得,等边三角形有什么性质?推论:等边三角形三个内角相等,每一个内角都等于60°.例2 ,已知:在△ABC中,AB=AC.小明想作∠BAC的角平分线,但他没有量角器,只有刻度尺,他如何作出∠BAC的角平分线?解:取BC得中点D,连接AD,那么AD平分∠BAC.△ABC中,因为AB=AC是底边上的中线,根据三线合一定理,AD是顶角的角平分线.∵AB=AC,AD=DC,AE=EB, ∴DC=BE,∠DCB=∠EBC. ∵BC=CB, ∴△BDC≌△CEB(SAS). ∴BD=CE.已知:AB=AC,AD=DC,AE=EB.
求证:BD=CE.证明:例3 证明:等腰三角形两腰上的中线相等.思考 :1、如图:ΔABC中,已知AB=AC∠B=∠C(在同一个三角形中,等边对等角).2、反过来:在ΔABC中,∠ B= ∠ C,AB=AC成立吗?ABC已知:ΔABC中,∠B=∠C求证:AB=AC证明:∴ ΔADB≌ ΔADC(AAS)∴AB=AC(全等三角形的对应边
相等)过A作ADBC,D为垂足,
∠ADB= ∠ADC=90 °.
在ΔADB和ΔADC中
∴∠B= ∠C
∠ADB= ∠ADCAD= AD
∴ AC=AB. ( )已知在一个三角形中,等角对等边定理:如果一个三角形有两个角相等,那么这个三角形是等腰三角形. 在△ABC中, ∵∠B=∠C ( )用符号语言表示为:这又是一个判定两条线段相等根据之一.例4 如图,∠A=72°,∠B=36°,CD平分∠ACB.试指出图中的哪些三角形是等腰三角形,并说明理由.解:△BAC,△DBC,△CAD为等腰三角形.∵∠ACB=180°-∠A-∠B
=180°-72°-36°=72°,∵CD平分∠ACB,∠ACD=∠BCD=36°,∴∠A=∠ACB=72° . ∴△BAC为等腰三角形.∴∠B=∠BCD=36°, ∴∠A=∠ADC=72° .∵△CAD为等腰三角形,∴△DBC为等腰三角形.∠ADC=180°-∠A-∠ACD
=180°-72°-36°
=72°推论1:证明已知:如图,ΔABC中, ∠ A=∠B=∠C
求证:AB=AC=BC证明:在ΔABC中
∵ ∠ A=∠B(已知)
∴BC=CA(等角对等边)
同理CA=AB
∴BC=CA=AB推论1.三个角都相等的三角形是等边三角形推论2:证明问题:如果一个等腰三角形中有一个角是60°,那么这个三角形是什么三角形?第一种情况:当顶角是60度时.
第二种情况:当底角是60度时.已知: ΔABC中,AB=AC, ∠B=60°.
求证:AB=AC=BC证明: ΔABC中
∵AB=AC,
∴ ∠B=∠C (等边对等角)
∵ ∠ B=60°
∴ ∠C = 60°
∴∠ A=60°
∴AB=AC=BC
有一个角是60°的等腰三角形是等边三角形.例5 如图,∠A=∠B,CE∥DA.求证:CE=CB.
需再增加什么条件,可使△BCE成为等边
三角形?证:∵CE∥DA,∴∠A=∠BEC.又∵∠A=∠B,∴∠B=∠BEC,∴△CBE为等腰三角形,∴CB=CE.要使△BCE为等边三角形,即只要满足CB=CE=BE=60°即可.则三角形的三条边应相等,1.判断下列语句是否正确.(1)等腰三角形的角平分线、中线和高互相重合.( )
(2)有一个角是60°的等腰三角形,其它两个内角也为60°. ( )
(3)等腰三角形的底角一定是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××证明:∵AE∥DC,∴∠C=∠AEB. ——①又∵AB=AE, ∴△ABE为等腰三角形,∴∠B=∠AEB. ——②由①②可得∠B=∠C.2.如图,点E在BC上,
AE∥DC,AB=AE.
求证:∠B=∠C. 有两边相等的三角形是等腰三角形2.等边对等角3. 三线合一2.等角对等边1.两边相等1.两腰相等小结
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
