2019-2020学年初一苏科版数学第六章《平面图形的认识(一)》检测卷(含答案)
文档属性
| 名称 | 2019-2020学年初一苏科版数学第六章《平面图形的认识(一)》检测卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 784.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-24 00:00:00 | ||
图片预览


文档简介
第六章《平面图形的认识(一)》检测卷
(总分:100分 时间:60分钟)
一、选择题(每小题2分,共20分)
1. 若,则的补角的度数为( )
A. 38° B. 48° C. 52° D. 128°
2.下列说法正确的是( )
A.射线与射线表示同一条射线
B.连接两点的线段叫作这两点的距离
C.平角是一条直线
D.若,,则
3.如图,是的平分线,是的平分线,且,则( )
A. 50° B. 75° C. 100° D. 120°
4.点在线段上,下列条件中不能确定点是线段中点的是( )
A. B.
C. D.
5.从南京开往南通的列车,途中停靠三个站点,如果任意两站间的票价都不同,不同的票价有( )
A. 6种 B. 10种 C. 12种 D. 14种
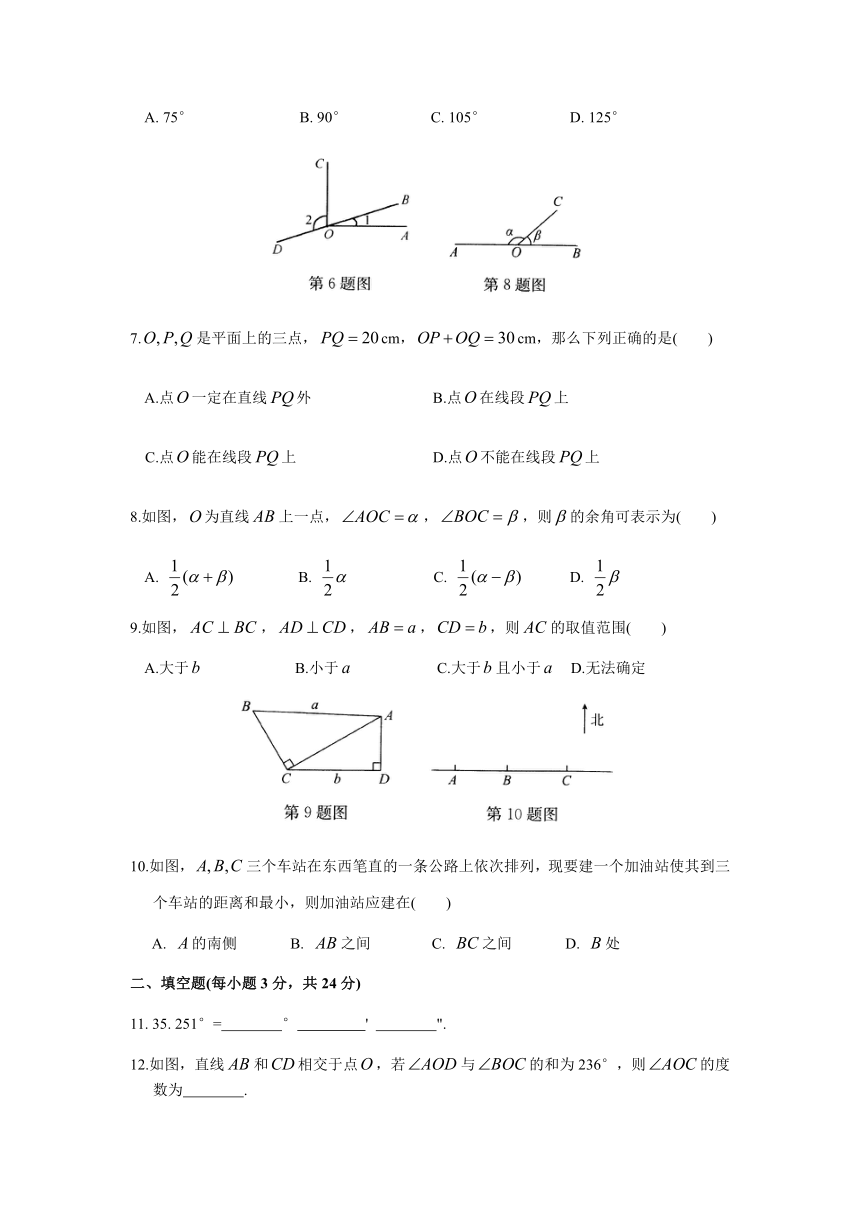
6.如图,点在同一直线上,若,,则的度数是( )
A. 75° B. 90° C. 105° D. 125°
7.是平面上的三点,cm,cm,那么下列正确的是( )
A.点一定在直线外 B.点在线段上
C.点能在线段上 D.点不能在线段上
8.如图,为直线上一点,,,则的余角可表示为( )
A. B. C. D.
9.如图,,,,,则的取值范围( )
A.大于 B.小于 C.大于且小于 D.无法确定
10.如图,三个车站在东西笔直的一条公路上依次排列,现要建一个加油站使其到三个车站的距离和最小,则加油站应建在( )
A. 的南侧 B. 之间 C. 之间 D. 处
二、填空题(每小题3分,共24分)
11. 35. 251°= ° ' ".
12.如图,直线和相交于点,若与的和为236°,则的度数为 .
13.如图,是线段上的一点,是线段的中点,若cm,cm,则的长是 .
14.一次测验从开始到结束,手表的时针转了50°的角,这次测验的时间是 .
15.如图,是直线上的点,平分,,则 .
16.如图,图中已标明了三组互相垂直的线段,那么点到的距离是 ,点到的距离是 .
17.平面内不同的两点确定一条直线,不同的三点最多确定三条直线.若平面内不同的个点最多可确定15条直线,则的值为 .
18.画一个,使,再作,,则的度数是 .
三、解答题(本大题共6小题,共56分)
19.(8分)如图,已知点,根据下列语句画图(尺规作图,要保留作图痕迹).
(1)画出直线;
(2)画出射线;
(3)在线段的延长线上截取线段,使得;
(4)画出线段.
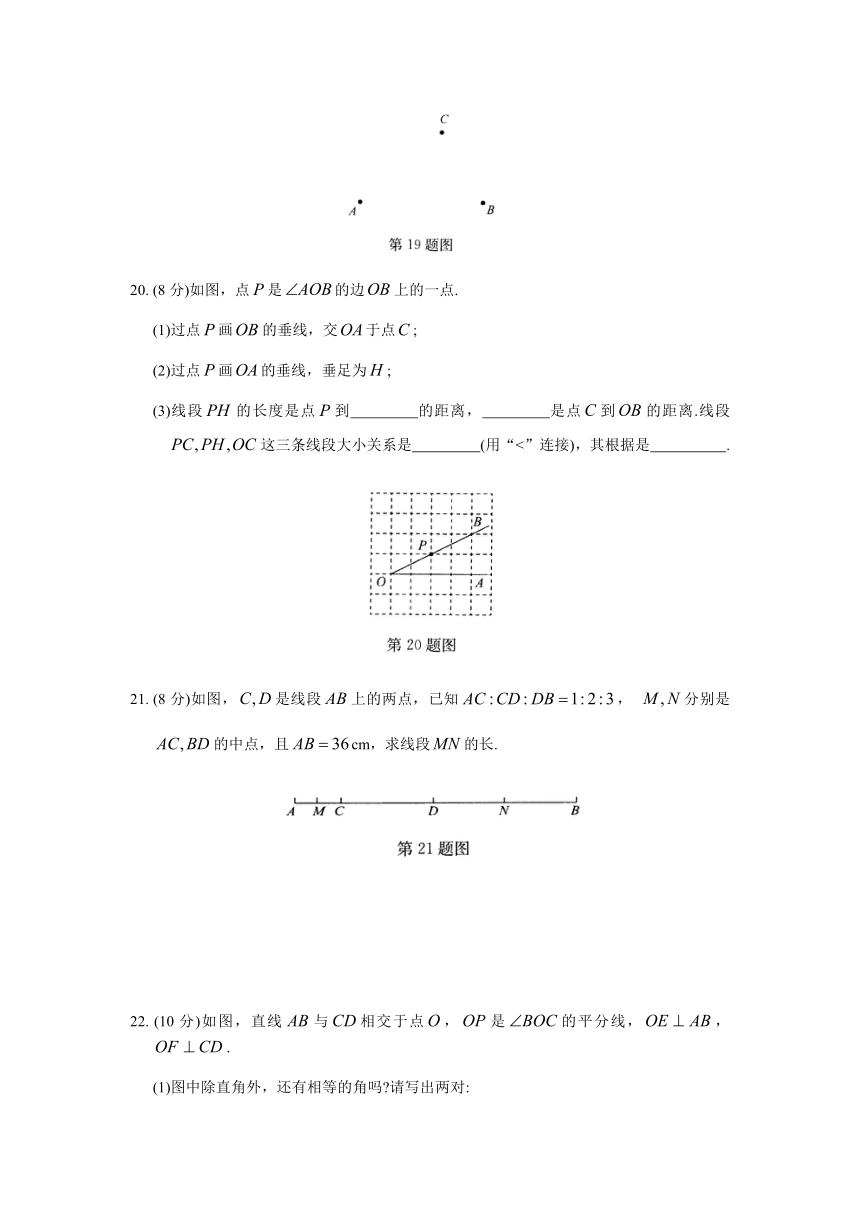
20. (8分)如图,点是的边上的一点.
(1)过点画的垂线,交于点;
(2)过点画的垂线,垂足为;
(3)线段的长度是点到 的距离, 是点到的距离.线段这三条线段大小关系是 (用“<”连接),其根据是 .
21. (8分)如图,是线段上的两点,已知, 分别是的中点,且cm,求线段的长.
22. (10分)如图,直线与相交于点,是的平分线,,.
(1)图中除直角外,还有相等的角吗?请写出两对:
① ;② .
(2)若,则① ;② ;
(3)与相等吗? ,理由是 .
(4)如果,求的度数.
23. (10分)如图,是线段上一动点,沿以2 cm/s的速度往返运动1次,是线段的中点,cm,设点运动时间为s().
(1)当时:
①求线段的长度;
②求线段的长度.
(2)用含的代数式表示运动过程中的长度.
(3)在运动过程中,若中点为,则的长是否变化?若不变,求出的长;若发生变化,请说明理由.
24. (12分)如图,直线与相交于点,,将一直角三角尺的直角顶点与重合,平分.
(1)求的度数;
(2)将三角尺以每秒3°的速度绕点顺时针旋转,同时直线也以每秒9°的速度绕点顺时针旋转,设运动时间为秒().
①当为何值时,直线平分 ;
②若直线平分,求出的值.
参考答案
一、选择题
1. D 2. D 3. C 4. B 5. B 6. B 7. D 8. C 9. C 10. D
二、填空题
11. 35 15 3.6
12. 62?
13. 8 cm
14. 100分钟
15. 70?
16. 的长 的长
17. 6
18. 30?或150?
三、解答题
19. 解:如图所示. (1) 直线即为所求.
(2)射线即为所求.
(3)点即为所求.
(4)线段即为所求.
20. (1) (2) 如图所示
(3) 线段的长度 垂线段最短
21. cm.
22. (1)① ②(答案不唯一)
(2)20? 70?
(3)相等 同角的余角相等
(4)
23.解:(1)①当时, cm.
②cm
(2)当时,;
当时,.
(3)不变.
∵中点为,是线段的中点,
∴ (cm)
24. (1)
(2)①分两种情况:
当平分 (如答图①)时,得
当平分(如答图②)时,得.
综上所述,当秒或32. 5秒时,直线平分.
②当平分(如答图③)时,得.
当平分(如答图④)时,得.
综上所述,若直线平分,的值为12秒或36秒.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
