人教版九年级数学上册教学讲义,复习补习资料(巩固练习):46【提高】《圆》全章复习与巩固含答案
文档属性
| 名称 | 人教版九年级数学上册教学讲义,复习补习资料(巩固练习):46【提高】《圆》全章复习与巩固含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 21:31:07 | ||
图片预览

文档简介
《圆》全章复习与巩固—知识讲解(提高)
【学习目标】
1.理解圆及其有关概念,理解弧、弦、圆心角的关系,探索并了解点与圆、直线与圆、圆与圆的位置关系,探索并掌握圆周角与圆心角的关系、直径所对的圆周角的特征;
2.了解切线的概念,探索并掌握切线与过切点的半径之间的位置关系,能判定一条直线是否为圆的切线,会过圆上一点画圆的切线;
3.了解三角形的内心和外心,探索如何过一点、两点和不在同一直线上的三点作圆;
4.了解正多边形的概念,掌握用等分圆周画圆的内接正多边形的方法;会计算弧长及扇形的面积、圆锥的侧面积及全面积;
5.结合相关图形性质的探索和证明,进一步培养合情推理能力,发展逻辑思维能力和推理论证的表达能力;通过这一章的学习,进一步培养综合运用知识的能力,运用学过的知识解决问题的能力.
【知识网络】
《圆》全章复习与巩固—巩固练习(提高)
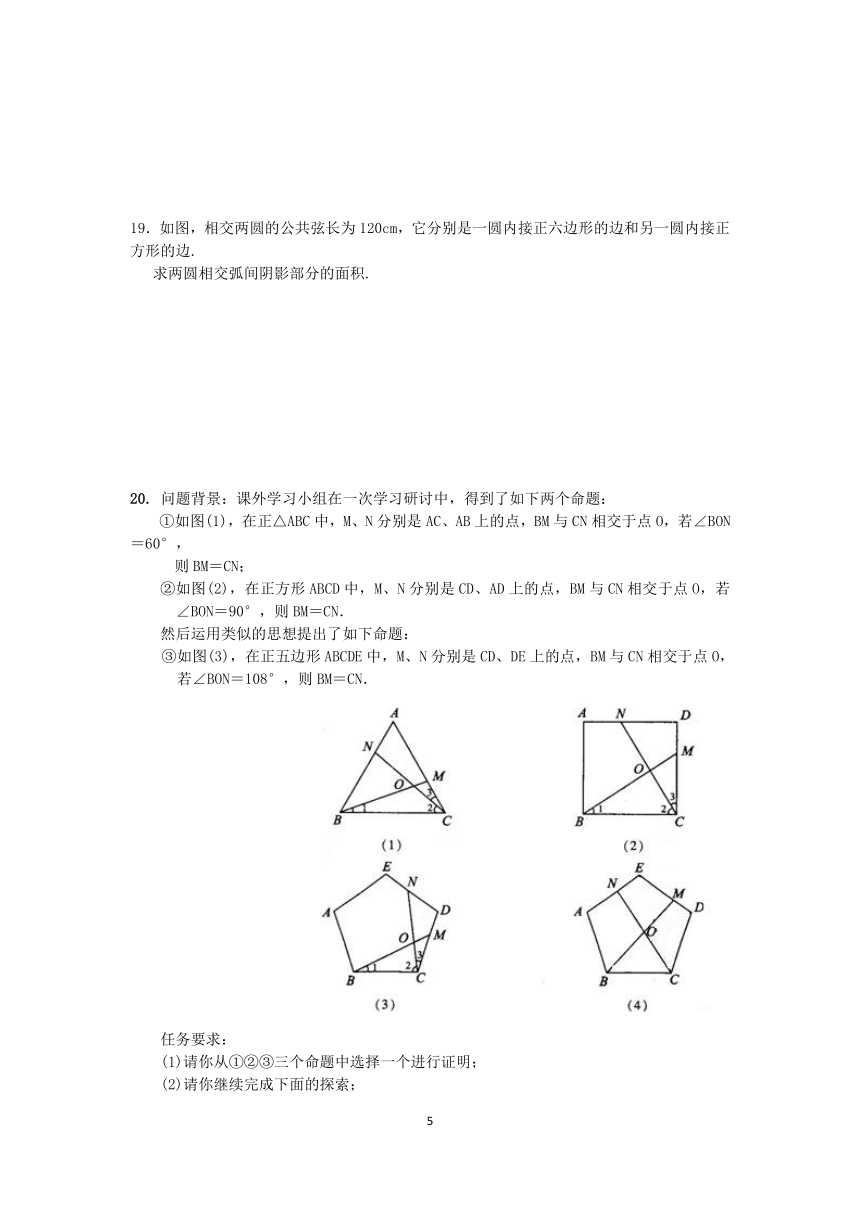
【巩固练习】
一、选择题
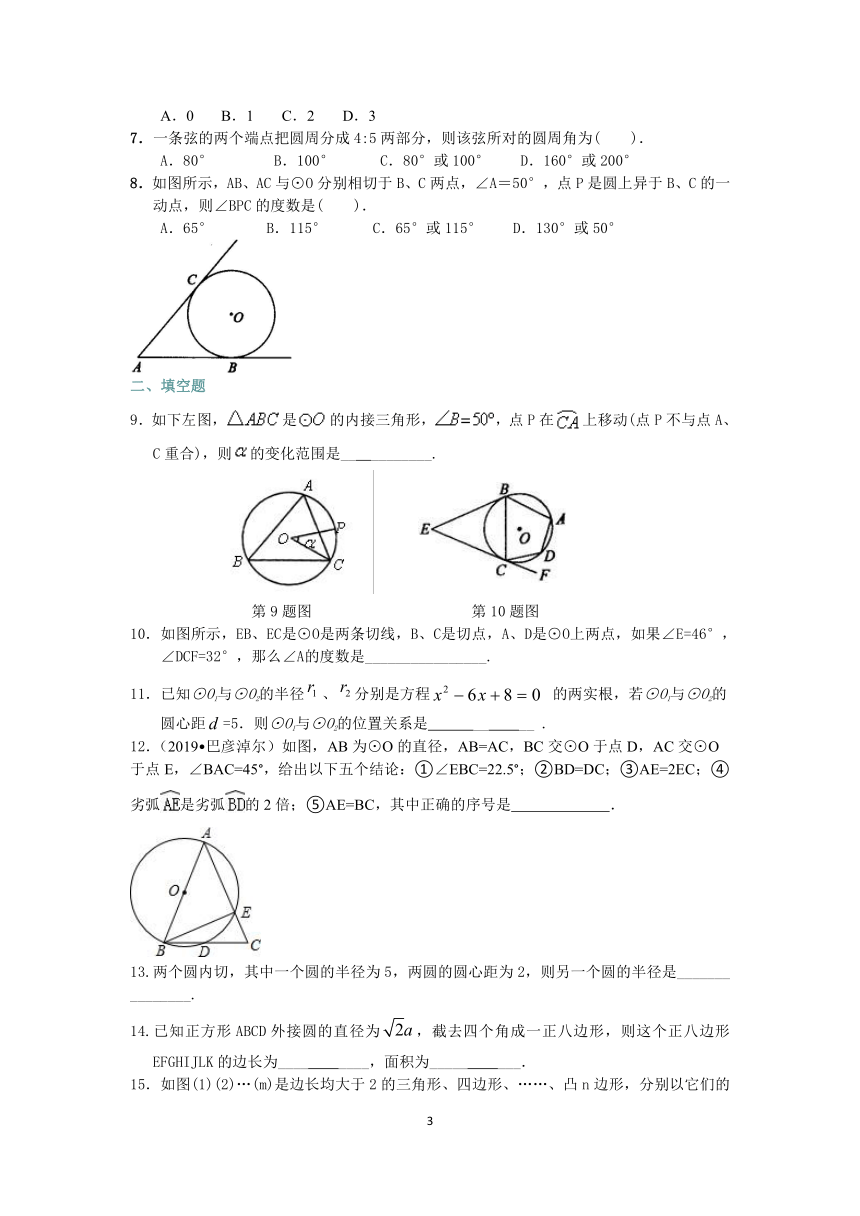
1.如图所示,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,
那么∠ADO等于(
).
A.70°
B.64°
C.62°
D.51°
2.在半径为27m的圆形广场中心点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图所示),则光源离地面的垂直高度SO为(
).
A.54m
B.m
C.m
D.m
第1题图
第2题图
第3题图
第4题图
3.设计一个商标图案,如图所示,在矩形ABCD中,AB=2BC,且AB=8cm,以A为圆心、AD的长为半径作半圆,则商标图案(阴影部分)的面积等于(
).
A.(4π+8)cm2
B.(4π+16)cm2
C.(3π+8)cm2
D.(3π+16)cm2
4.如图,的半径为5,弦的长为8,点在线段(包括端点)上移动,则的取值范围是(
).
A.
B.
C.
D.
5.
“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”用数学语言可表示为:如图所示,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为(
)
A.12.5寸
B.13寸
C.25寸
D.26寸
6.(2019 贵港)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A.0
B.1
C.2
D.3
7.一条弦的两个端点把圆周分成4:5两部分,则该弦所对的圆周角为(
).
A.80°
B.100°
C.80°或100°
D.160°或200°
8.如图所示,AB、AC与⊙O分别相切于B、C两点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是(
).
A.65°
B.115°
C.65°或115°
D.130°或50°
二、填空题
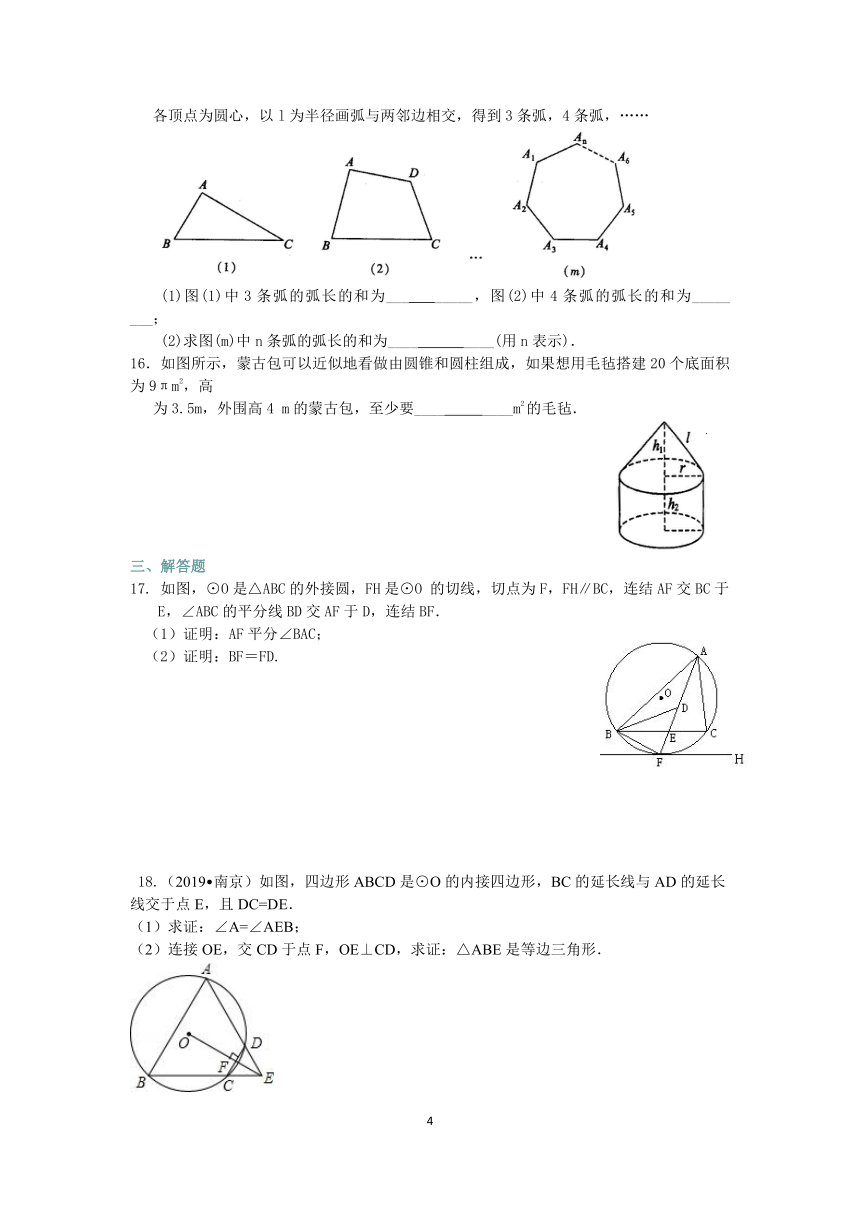
9.如下左图,是的内接三角形,,点P在上移动(点P不与点A、C重合),则的变化范围是__
________.
第9题图
第10题图
10.如图所示,EB、EC是⊙O是两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,那么∠A的度数是________________.
11.已知⊙O1与⊙O2的半径、分别是方程
的两实根,若⊙O1与⊙O2的圆心距=5.则⊙O1与⊙O2的位置关系是
__
__
.
12.(2019 巴彦淖尔)如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC,其中正确的序号是
.
13.两个圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径是_______
________.
14.已知正方形ABCD外接圆的直径为,截去四个角成一正八边形,则这个正八边形EFGHIJLK的边长为____
____,面积为_____
___.
15.如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n边形,分别以它们的各顶点为圆心,以l为半径画弧与两邻边相交,得到3条弧,4条弧,……
(1)图(1)中3条弧的弧长的和为___
_____,图(2)中4条弧的弧长的和为_____
___;
(2)求图(m)中n条弧的弧长的和为____
____(用n表示).
16.如图所示,蒙古包可以近似地看做由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为9πm2,高
为3.5m,外围高4
m的蒙古包,至少要____
____m2的毛毡.
三、解答题
17.
如图,⊙O是△ABC的外接圆,FH是⊙O
的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD.
18.(2019 南京)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.
求两圆相交弧间阴影部分的面积.
20.
问题背景:课外学习小组在一次学习研讨中,得到了如下两个命题:
①如图(1),在正△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,
则BM=CN;
②如图(2),在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类似的思想提出了如下命题:
③如图(3),在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.
任务要求:
(1)请你从①②③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索;
①在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明);
②如图(4),在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否成立.若成立,请给予证明;若不成立,请说明理由.
【答案与解析】
一、选择题
1.【答案】B;
【解析】由AB为⊙O的切线,则AB⊥OD.又BD=OB,则AB垂直平分OD,AO=AD,∠DAB=∠BAO.
由AB、AC为⊙O的切线,则∠CAO=∠BAO=∠DAB.所以,∠DAB=∠DAC=26°.
∠ADO=90°-26°=64°.
本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等.
2.【答案】C;
【解析】圆锥的高、底面半径与母线组成直角三角形.
由题意,SO⊥AB于O,∴
∠SOA=∠SOB=90°.又SA=SB,∠ASB=120°,
∴
∠SAB=∠SBA=,设SO=x
m,则AS=2x
m.∵
AO=27,
由勾股定理,得(2x)2-x2=272,解得(m).
3.【答案】A.;
【解析】对图中阴影部分进行分析,可看做扇形、矩形、三角形的面积和差关系.
∵
矩形ABCD中,AB=2BC,AB=8cm,
∴
AD=BC=4cm,∠DAF=90°,
,,
又AF=AD=4cm,
∴
,
∴
.
4.【答案】A;
【解析】OM最长是半径5;最短是OM⊥AB时,此时OM=3,故选A.
5.【答案】D;
【解析】因为直径CD垂直于弦AB,所以可通过连接OA(或OB),求出半径即可.
根据“垂直于弦的直径平分弦,并且平分弦所对的两条弧”,
知(寸),在Rt△AOE中,,
即,解得OA=13,进而求得CD=26(寸).
故选D.
6.【答案】B.
【解析】设OP与⊙O交于点N,连结MN,OQ,如图,
∵OP=4,ON=2,
∴N是OP的中点,
∵M为PQ的中点,
∴MN为△POQ的中位线,
∴MN=OQ=×2=1,
∴点M在以N为圆心,1为半径的圆上,
当点M在ON上时,OM最小,最小值为1,
∴线段OM的最小值为1.故选B.
7.【答案】C;
【解析】圆周角的顶点在劣弧上时,圆周角为;圆周角的顶点在优弧上时,
圆周角为.注意分情况讨论.
8.【答案】C;
【解析】连接OC、OB,则∠BOC=360°-90°-90°-50°=130°.点P在优弧上时,
∠BPC=∠BOC=65°;点P在劣弧上时,∠BPC=180°-65°=115°.
主要应用了切线的性质定理、圆周角定理和多边形内角和定理.
二、填空题
9.【答案】;
10.【答案】99°;
【解析】由EB=EC,∠E=46°知,∠ECB=
67°,从而∠BCD=180°-67°-32°=81°,
在⊙O中,∠BCD与∠A互补,所以∠A=180°-81°=99°.
11.【答案】相交;
【解析】求出方程
的两实根、分别是4、2,则-<<+,所以两圆相交.
12.【答案】①②④;
【解析】连接AD,AB是直径,
则AD⊥BC,
又∵△ABC是等腰三角形,
故点D是BC的中点,即BD=CD,故②正确;
∵AD是∠BAC的平分线,
由圆周角定理知,∠EBC=∠DAC=∠BAC=22.5°,故①正确;
∵∠ABE=90°﹣∠EBC﹣∠BAD=45°=2∠CAD,故④正确;
∵∠EBC=22.5°,2EC≠BE,AE=BE,∴AE≠2CE,③不正确;
∵AE=BE,BE是直角边,BC是斜边,肯定不等,故⑤错误.
综上所述,正确的结论是:①②④.
13.【答案】7或3;
【解析】两圆有三种位置关系:相交、相切(外切、内切)和相离(外离、内含).两圆内切时,
圆心距,题中一圆半径为5,而d=2,所以有,解得r=7或r=3,
即另一圆半径为7或3.
14.【答案】;
;
【解析】正方形ABCD外接圆的直径就是它的对角线,由此求得正方形边长为a.如图所示,设正八边形的边长为x.在Rt△AEL中,LE=x,AE=AL=,∴
,,
即正八边形的边长为.
.
15.【答案】(1)π;
2π;
(2)(n-2)π;
【解析】∵
n边形内角和为(n-2)180°,前n条弧的弧长的和为个以某定点为圆心,以1为半径的圆周长,∴
n条弧的弧长的和为.
本题还有其他解法,比如:设各个扇形的圆心角依次为,,…,,
则,
∴
n条弧长的和为
.
16.【答案】720π;
【解析】∵
S=πr2,∴
9π=πr2,∴
r=3.∴
h1=4,∴
,
∴
,
.
所求面积包括圆锥的侧面积和圆柱的侧面积,不包括底面积.
三、解答题
17.【答案与解析】
(1)连结OF
∵FH是⊙O的切线
∴OF⊥FH
∵FH∥BC
,
∴OF垂直平分BC
∴
∴AF平分∠BAC
.
(2)由(1)及题设条件可知
∠1=∠2,∠4=∠3,∠5=∠2
∴∠1+∠4=∠2+∠3
∴∠1+∠4=∠5+∠3
∠FDB=∠FBD
∴BF=FD.
18.【答案与解析】
证明:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠AEB,
∴∠A=∠AEB;
(2)∵∠A=∠AEB,
∴△ABE是等腰三角形,
∵EO⊥CD,
∴CF=DF,
∴EO是CD的垂直平分线,
∴ED=EC,
∵DC=DE,
∴DC=DE=EC,
∴△DCE是等边三角形,
∴∠AEB=60°,
∴△ABE是等边三角形.
19.【答案与解析】
解:∵公共弦AB=120
.
20.
【答案与解析】
(1)如选命题①.
证明:在图(1)中,
∵
∠BON=60°,∴
∠1+∠2=60°.
∵
∠3+∠2=60°,∴
∠1=∠3.
又∵
BC=CA,∠BCM=∠CAN=60°,
∴
△BCM≌△CAN,∴
BM=CM.
如选命题②.
证明:在图(2)中,
∵
∠BON=90°,∴
∠1+∠2=90°.
∵
∠3+∠2=90°,∴
∠1=∠3.
又∵
BC=CD,∠BCM=∠CDN=90°,
∴
△BCM≌△CDN,∴
BM=CN.
如选命题③.
证明:在图(3)中,
∵
∠BON=108°,∴
∠1+∠2=108°.
∵
∠2+∠3=108°,∴
∠1=∠3.
又∵
BC=CD,∠BCM=∠CDN=108°,
∴
△BCM≌△CDN,∴
BM=CN.
(2)①答:当∠BON=时结论BM=CN成立.
②答:当∠BON=108°时.BM=CN还成立.
证明:如图(4),连接BD、CE
在△BCD和△CDE中,
∵
BC=CD,∠BCD=∠CDE=108°,CD=DE,
∴
△BCD≌△CDE.
∴
BD=CE,∠BDC=∠CED,∠DBC=∠ECD.
∵
∠CDE=∠DEN=108°,
∴
∠BDM=∠CEM.
∵
∠OBC+∠OCB=108°,∠OCB+∠OCD=108°.
∴
∠MBC=∠NCD.
又∵
∠DBC=∠ECD=36°,
∴
∠DBM=∠ECM.
∴
△BDM≌△CEN,
∴
BM=CN.
11
【学习目标】
1.理解圆及其有关概念,理解弧、弦、圆心角的关系,探索并了解点与圆、直线与圆、圆与圆的位置关系,探索并掌握圆周角与圆心角的关系、直径所对的圆周角的特征;
2.了解切线的概念,探索并掌握切线与过切点的半径之间的位置关系,能判定一条直线是否为圆的切线,会过圆上一点画圆的切线;
3.了解三角形的内心和外心,探索如何过一点、两点和不在同一直线上的三点作圆;
4.了解正多边形的概念,掌握用等分圆周画圆的内接正多边形的方法;会计算弧长及扇形的面积、圆锥的侧面积及全面积;
5.结合相关图形性质的探索和证明,进一步培养合情推理能力,发展逻辑思维能力和推理论证的表达能力;通过这一章的学习,进一步培养综合运用知识的能力,运用学过的知识解决问题的能力.
【知识网络】
《圆》全章复习与巩固—巩固练习(提高)
【巩固练习】
一、选择题
1.如图所示,AB、AC为⊙O的切线,B和C是切点,延长OB到D,使BD=OB,连接AD.如果∠DAC=78°,
那么∠ADO等于(
).
A.70°
B.64°
C.62°
D.51°
2.在半径为27m的圆形广场中心点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图所示),则光源离地面的垂直高度SO为(
).
A.54m
B.m
C.m
D.m
第1题图
第2题图
第3题图
第4题图
3.设计一个商标图案,如图所示,在矩形ABCD中,AB=2BC,且AB=8cm,以A为圆心、AD的长为半径作半圆,则商标图案(阴影部分)的面积等于(
).
A.(4π+8)cm2
B.(4π+16)cm2
C.(3π+8)cm2
D.(3π+16)cm2
4.如图,的半径为5,弦的长为8,点在线段(包括端点)上移动,则的取值范围是(
).
A.
B.
C.
D.
5.
“圆材埋壁”是我国古代著名的数学著作《九章算术》中的问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何 ”用数学语言可表示为:如图所示,CD为⊙O的直径,弦AB⊥CD于E,CE=1寸,AB=10寸,则直径CD的长为(
)
A.12.5寸
B.13寸
C.25寸
D.26寸
6.(2019 贵港)如图,已知P是⊙O外一点,Q是⊙O上的动点,线段PQ的中点为M,连接OP,OM.若⊙O的半径为2,OP=4,则线段OM的最小值是( )
A.0
B.1
C.2
D.3
7.一条弦的两个端点把圆周分成4:5两部分,则该弦所对的圆周角为(
).
A.80°
B.100°
C.80°或100°
D.160°或200°
8.如图所示,AB、AC与⊙O分别相切于B、C两点,∠A=50°,点P是圆上异于B、C的一动点,则∠BPC的度数是(
).
A.65°
B.115°
C.65°或115°
D.130°或50°
二、填空题
9.如下左图,是的内接三角形,,点P在上移动(点P不与点A、C重合),则的变化范围是__
________.
第9题图
第10题图
10.如图所示,EB、EC是⊙O是两条切线,B、C是切点,A、D是⊙O上两点,如果∠E=46°,∠DCF=32°,那么∠A的度数是________________.
11.已知⊙O1与⊙O2的半径、分别是方程
的两实根,若⊙O1与⊙O2的圆心距=5.则⊙O1与⊙O2的位置关系是
__
__
.
12.(2019 巴彦淖尔)如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC,其中正确的序号是
.
13.两个圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径是_______
________.
14.已知正方形ABCD外接圆的直径为,截去四个角成一正八边形,则这个正八边形EFGHIJLK的边长为____
____,面积为_____
___.
15.如图(1)(2)…(m)是边长均大于2的三角形、四边形、……、凸n边形,分别以它们的各顶点为圆心,以l为半径画弧与两邻边相交,得到3条弧,4条弧,……
(1)图(1)中3条弧的弧长的和为___
_____,图(2)中4条弧的弧长的和为_____
___;
(2)求图(m)中n条弧的弧长的和为____
____(用n表示).
16.如图所示,蒙古包可以近似地看做由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为9πm2,高
为3.5m,外围高4
m的蒙古包,至少要____
____m2的毛毡.
三、解答题
17.
如图,⊙O是△ABC的外接圆,FH是⊙O
的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.
(1)证明:AF平分∠BAC;
(2)证明:BF=FD.
18.(2019 南京)如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
19.如图,相交两圆的公共弦长为120cm,它分别是一圆内接正六边形的边和另一圆内接正方形的边.
求两圆相交弧间阴影部分的面积.
20.
问题背景:课外学习小组在一次学习研讨中,得到了如下两个命题:
①如图(1),在正△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°,
则BM=CN;
②如图(2),在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90°,则BM=CN.
然后运用类似的思想提出了如下命题:
③如图(3),在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.
任务要求:
(1)请你从①②③三个命题中选择一个进行证明;
(2)请你继续完成下面的探索;
①在正n(n≥3)边形ABCDEF…中,M、N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM=CN成立(不要求证明);
②如图(4),在正五边形ABCDE中,M、N分别是DE、AE上的点,BM与CN相交于点O,∠BON=108°时,试问结论BM=CN是否成立.若成立,请给予证明;若不成立,请说明理由.
【答案与解析】
一、选择题
1.【答案】B;
【解析】由AB为⊙O的切线,则AB⊥OD.又BD=OB,则AB垂直平分OD,AO=AD,∠DAB=∠BAO.
由AB、AC为⊙O的切线,则∠CAO=∠BAO=∠DAB.所以,∠DAB=∠DAC=26°.
∠ADO=90°-26°=64°.
本题涉及切线性质定理、切线长定理、垂直平分线的性质、等腰三角形的性质等.
2.【答案】C;
【解析】圆锥的高、底面半径与母线组成直角三角形.
由题意,SO⊥AB于O,∴
∠SOA=∠SOB=90°.又SA=SB,∠ASB=120°,
∴
∠SAB=∠SBA=,设SO=x
m,则AS=2x
m.∵
AO=27,
由勾股定理,得(2x)2-x2=272,解得(m).
3.【答案】A.;
【解析】对图中阴影部分进行分析,可看做扇形、矩形、三角形的面积和差关系.
∵
矩形ABCD中,AB=2BC,AB=8cm,
∴
AD=BC=4cm,∠DAF=90°,
,,
又AF=AD=4cm,
∴
,
∴
.
4.【答案】A;
【解析】OM最长是半径5;最短是OM⊥AB时,此时OM=3,故选A.
5.【答案】D;
【解析】因为直径CD垂直于弦AB,所以可通过连接OA(或OB),求出半径即可.
根据“垂直于弦的直径平分弦,并且平分弦所对的两条弧”,
知(寸),在Rt△AOE中,,
即,解得OA=13,进而求得CD=26(寸).
故选D.
6.【答案】B.
【解析】设OP与⊙O交于点N,连结MN,OQ,如图,
∵OP=4,ON=2,
∴N是OP的中点,
∵M为PQ的中点,
∴MN为△POQ的中位线,
∴MN=OQ=×2=1,
∴点M在以N为圆心,1为半径的圆上,
当点M在ON上时,OM最小,最小值为1,
∴线段OM的最小值为1.故选B.
7.【答案】C;
【解析】圆周角的顶点在劣弧上时,圆周角为;圆周角的顶点在优弧上时,
圆周角为.注意分情况讨论.
8.【答案】C;
【解析】连接OC、OB,则∠BOC=360°-90°-90°-50°=130°.点P在优弧上时,
∠BPC=∠BOC=65°;点P在劣弧上时,∠BPC=180°-65°=115°.
主要应用了切线的性质定理、圆周角定理和多边形内角和定理.
二、填空题
9.【答案】;
10.【答案】99°;
【解析】由EB=EC,∠E=46°知,∠ECB=
67°,从而∠BCD=180°-67°-32°=81°,
在⊙O中,∠BCD与∠A互补,所以∠A=180°-81°=99°.
11.【答案】相交;
【解析】求出方程
的两实根、分别是4、2,则-<<+,所以两圆相交.
12.【答案】①②④;
【解析】连接AD,AB是直径,
则AD⊥BC,
又∵△ABC是等腰三角形,
故点D是BC的中点,即BD=CD,故②正确;
∵AD是∠BAC的平分线,
由圆周角定理知,∠EBC=∠DAC=∠BAC=22.5°,故①正确;
∵∠ABE=90°﹣∠EBC﹣∠BAD=45°=2∠CAD,故④正确;
∵∠EBC=22.5°,2EC≠BE,AE=BE,∴AE≠2CE,③不正确;
∵AE=BE,BE是直角边,BC是斜边,肯定不等,故⑤错误.
综上所述,正确的结论是:①②④.
13.【答案】7或3;
【解析】两圆有三种位置关系:相交、相切(外切、内切)和相离(外离、内含).两圆内切时,
圆心距,题中一圆半径为5,而d=2,所以有,解得r=7或r=3,
即另一圆半径为7或3.
14.【答案】;
;
【解析】正方形ABCD外接圆的直径就是它的对角线,由此求得正方形边长为a.如图所示,设正八边形的边长为x.在Rt△AEL中,LE=x,AE=AL=,∴
,,
即正八边形的边长为.
.
15.【答案】(1)π;
2π;
(2)(n-2)π;
【解析】∵
n边形内角和为(n-2)180°,前n条弧的弧长的和为个以某定点为圆心,以1为半径的圆周长,∴
n条弧的弧长的和为.
本题还有其他解法,比如:设各个扇形的圆心角依次为,,…,,
则,
∴
n条弧长的和为
.
16.【答案】720π;
【解析】∵
S=πr2,∴
9π=πr2,∴
r=3.∴
h1=4,∴
,
∴
,
.
所求面积包括圆锥的侧面积和圆柱的侧面积,不包括底面积.
三、解答题
17.【答案与解析】
(1)连结OF
∵FH是⊙O的切线
∴OF⊥FH
∵FH∥BC
,
∴OF垂直平分BC
∴
∴AF平分∠BAC
.
(2)由(1)及题设条件可知
∠1=∠2,∠4=∠3,∠5=∠2
∴∠1+∠4=∠2+∠3
∴∠1+∠4=∠5+∠3
∠FDB=∠FBD
∴BF=FD.
18.【答案与解析】
证明:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠AEB,
∴∠A=∠AEB;
(2)∵∠A=∠AEB,
∴△ABE是等腰三角形,
∵EO⊥CD,
∴CF=DF,
∴EO是CD的垂直平分线,
∴ED=EC,
∵DC=DE,
∴DC=DE=EC,
∴△DCE是等边三角形,
∴∠AEB=60°,
∴△ABE是等边三角形.
19.【答案与解析】
解:∵公共弦AB=120
.
20.
【答案与解析】
(1)如选命题①.
证明:在图(1)中,
∵
∠BON=60°,∴
∠1+∠2=60°.
∵
∠3+∠2=60°,∴
∠1=∠3.
又∵
BC=CA,∠BCM=∠CAN=60°,
∴
△BCM≌△CAN,∴
BM=CM.
如选命题②.
证明:在图(2)中,
∵
∠BON=90°,∴
∠1+∠2=90°.
∵
∠3+∠2=90°,∴
∠1=∠3.
又∵
BC=CD,∠BCM=∠CDN=90°,
∴
△BCM≌△CDN,∴
BM=CN.
如选命题③.
证明:在图(3)中,
∵
∠BON=108°,∴
∠1+∠2=108°.
∵
∠2+∠3=108°,∴
∠1=∠3.
又∵
BC=CD,∠BCM=∠CDN=108°,
∴
△BCM≌△CDN,∴
BM=CN.
(2)①答:当∠BON=时结论BM=CN成立.
②答:当∠BON=108°时.BM=CN还成立.
证明:如图(4),连接BD、CE
在△BCD和△CDE中,
∵
BC=CD,∠BCD=∠CDE=108°,CD=DE,
∴
△BCD≌△CDE.
∴
BD=CE,∠BDC=∠CED,∠DBC=∠ECD.
∵
∠CDE=∠DEN=108°,
∴
∠BDM=∠CEM.
∵
∠OBC+∠OCB=108°,∠OCB+∠OCD=108°.
∴
∠MBC=∠NCD.
又∵
∠DBC=∠ECD=36°,
∴
∠DBM=∠ECM.
∴
△BDM≌△CEN,
∴
BM=CN.
11
同课章节目录
