人教版九年级数学上册教学讲义,复习补习资料(巩固练习):29【提高】《旋转》全章复习与巩固含答案
文档属性
| 名称 | 人教版九年级数学上册教学讲义,复习补习资料(巩固练习):29【提高】《旋转》全章复习与巩固含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 155.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 21:30:14 | ||
图片预览



文档简介
《旋转》全章复习与巩固(提高)知识讲解
【学习目标】
1、
通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质.
2、通过具体实例认识中心对称,探索它的基本性质,理解对应点所连线段被对称中心平分的性质,了解平行四边形、圆是中心对称图形.
3、
能够按要求作出简单平面图形旋转后的图形,欣赏旋转在现实生活中的应用.
4、探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用轴对称、平移和旋转的组合进行图案设计.
【知识网络】
【巩固练习】
一、选择题
1.在下列四个图案中,既是轴对称图形,又是中心对称图形的是(
).
2.
时钟钟面上的分针从12时开始绕中心旋转120°,则下列说法正确的是( ).
A.此时分针指向的数字为3 B.此时分针指向的数字为6
C.此时分针指向的数字为4 D.分针转动3,但时针却未改变
3.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( ).
A.M或O或N
B.E或O或C
C.E或O或N
D.M或O或C
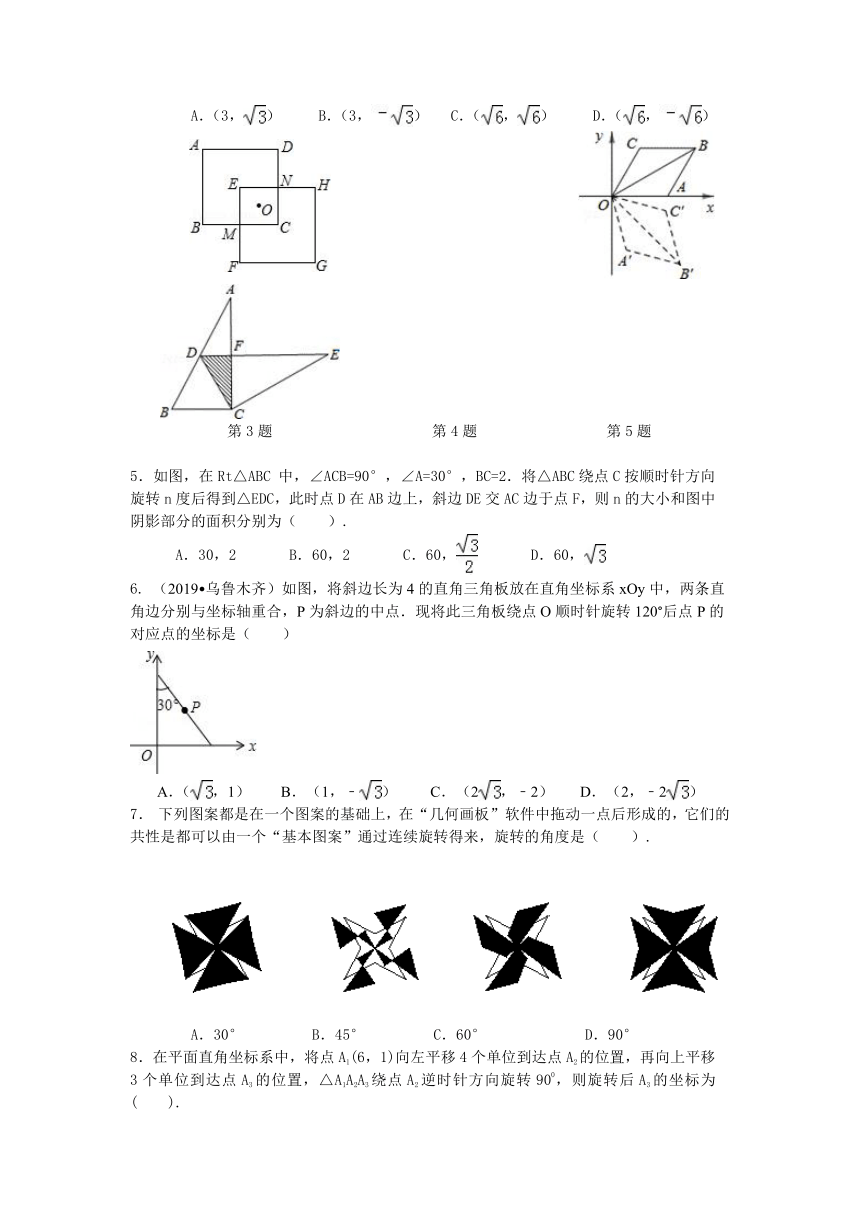
4.如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB=,∠C=120°,则点B′的坐标为( ).
A.(3,)
B.(3,)
C.(,)
D.(,)
第3题
第4题
第5题
5.如图,在Rt△ABC
中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( ).
A.30,2
B.60,2
C.60,
D.60,
6.
(2019 乌鲁木齐)如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
A.(,1)
B.
(1,﹣)
C.
(2,﹣2)
D.
(2,﹣2)
7.
下列图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们的共性是都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( ).
A.30°
B.45°
C.60°
D.90°
8.在平面直角坐标系中,将点A1(6,1)向左平移4个单位到达点A2的位置,再向上平移3个单位到达点A3的位置,△A1A2A3绕点A2逆时针方向旋转900,则旋转后A3的坐标为(
).
A.(-2,1)
B.(1,1)
C.(-1,1)
D.(5,1)
二.
填空题
9.
(2019 扬州)如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= .
10.如图,正方形ABCD的边长为4cm,正方形AEFG的边长为1cm.如果正方形AEFG绕点A旋转,那么C、F两点之间的最小距离为 _________ cm.
11.绕一定点旋转180°后与原来图形重合的图形是中心对称图形,正六边形就是这样的图形.小明发现将正六边形绕着它的中心旋转一个小于180°的角,也可以使它与原来的正六边形重合,请你写出小明发现的一个旋转角的度数:_____________________.
12.如图所示,在Rt△ABC中,∠A=90°,AB=AC=4cm,以斜边BC上距离B点 cm的H为中心,把这个三角形按逆时针方向旋转90°至△DEF,则旋转前后两个直角三角形重叠部分的面积是___cm2.
13.如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至ED,连接AE、DE,△ADE的面积为3,则BC的长为_________.
14.
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP绕点A逆时针旋转后与△ACP′重合,如果AP=3,那么线段PP′的长等于________.
15.如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…,则:
(1)点P5的坐标为__________;
(2)落在x轴正半轴上的点Pn坐标是_________,其中n满足的条件是________.
16.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是__________.
三
综合题
17.
如图,已知,点P是正方ABCD内一点,且AP∶BP∶CP=1∶2∶3.
求证:∠APB=135°.
18.如图,已知点D是△ABC的BC边的中点,E、F分别是AB、AC上的点,且DE⊥DF.
求证:
BE
+
CF>EF
19.
(2019 黄冈中学自主招生)阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
请你回答:AP的最大值是
.
参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是
.(结果可以不化简)
20.如图14―1,14―2,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.
⑴如图14―1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是
;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是
;
③请证明你的上述两猜想.
⑵如图14―2,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系.
【答案与解析】
一、选择题
1.【答案】C.
2.【答案】C.
【解析】分针每5分钟转动30.
3.【答案】A.
【解析】
因为以M或O或N为旋转中心两个图形能够完全重合.
4.【答案】D.
【解析】因为是菱形,所以可得为等腰直角三角形.
5.【答案】C.
【解析】△BDC为正三角形,所以△FDC为直角三角形,∠DCF=30°,DF=1,FC=,即求得.
6.【答案】B.
【解析】根据题意画出△AOB绕着O点顺时针旋转120°得到的△COD,连接OP,OQ,过Q作QM⊥y轴,
∴∠POQ=120°,
∵AP=OP,
∴∠BAO=∠POA=30°,
∴∠MOQ=30°,
在Rt△OMQ中,OQ=OP=2,
∴MQ=1,OM=,
则P的对应点Q的坐标为(1,﹣),故选B
7.【答案】D.
8.【答案】C.
【解析】即旋转90°后坐标为(-1,1).
二、填空题
9.【答案】5.
【解析】作FG⊥AC,
根据旋转的性质,EC=BC=4,DC=AC=6,∠ACD=∠ACB=90°,
∵点F是DE的中点,
∴FG∥CD
∴GF=CD=AC=3
EG=EC=BC=2
∵AC=6,EC=BC=4
∴AE=2
∴AG=4
根据勾股定理,AF=5.
10.【答案】;
【解析】当点F在正方形ABCD的对角线AC上时,CF=AC﹣AF,当点F不在正方形的对角线上时由三角形的三边关系可知AC﹣AF<CF<AC+AF,
∴当点F在正方形ABCD的对角线AC上时,C、F两点之间的距离最小,
∴CF=AC﹣AF=4﹣=cm.
故答案为:.
11.【答案】60°或120°.
【解析】正六边形的中心角是60°.
12.【答案】1.
【解析】证明△FHC和△FHG是等腰直角三角形,且腰长为,即得.
13.【答案】5.
【解析】做DF⊥BC,EG⊥AD,交AD的延长线于点G
,则AD=BF,
可证得△DEG≌△DCF,即EG=FC,又因为,所以EG=3,
即BC=BF+FC=AD+EG=5.
14.【答案】.
【解析】由旋转可知△APP′是等腰直角三角形,所以PP′=.
15.【答案】(1)
,
(2)落在x轴正半轴上的点Pn坐标是,其中n满足的条件是n=8k(k=0,1,2,…)
16.【答案】(-1,).
【解析】首先求得的坐标,即可求得坐标.
三.解答题
17.【解析】证明:将△APB绕点B沿顺时针方向旋转90°至△CP′B
位置(如图),
则有△APB≌△CP′B.
∴BP′=
BP,CP′=AP,
∠PBP′=
90°,∠APB=∠CP′B.
设CP′=
AP=
k,则BP′=
BP=2k,CP=
3k,在Rt△BP′P中,
BP′=
BP=
2k,∴∠BP′P=45°.
=(3k)2=
CP2,
∴∠CP′P=90°,
∴∠CP′B=∠CP′P+∠BP′P=90°+45°=135°,
即∠APB=135°.
18.【解析】证明:将△BDE绕点D沿顺时针方向旋转180°至△CDG位置,则有△BDE≌△CDG.
∴BE=CG,ED=DG.
∵DE⊥DF,即
DF⊥EG.
∴EF=FG,在△FCG中CG+CF>FG,
即BE+CF>EF.
19.【解析】解:(1)如图2,∵△ABP逆时针旋转60°得到△A′BC,
∴∠A′BA=60°,A′B=AB,AP=A′C
∴△A′BA是等边三角形,
∴A′A=AB=BA′=2,
在△AA′C中,A′C<AA′+AC,即AP<6,
则当点A′A、C三点共线时,A′C=AA′+AC,即AP=6,即AP的最大值是:6;
故答案是:6.
(2)如图3,∵Rt△ABC是等腰三角形,∴AB=BC.
以B为中心,将△APB逆时针旋转60°得到△A'P'B.则A'B=AB=BC=4,PA=P′A′,PB=P′B,
∴PA+PB+PC=P′A′+P'B+PC.
∵当A'、P'、P、C四点共线时,(P'A+P'B+PC)最短,即线段A'C最短,
∴A'C=PA+PB+PC,
∴A'C长度即为所求.
过A'作A'D⊥CB延长线于D.
∵∠A'BA=60°(由旋转可知),
∴∠1=30°.
∵A'B=4,
∴A'D=2,BD=2,
∴CD=4+2.
在Rt△A'DC中A'C====2+2;
∴AP+BP+CP的最小值是:2+2(或不化简为).
故答案是:2+2(或不化简为).
20.【解析】
⑴ ①DE=EF;
②NE=BF.
③证明:
∵四边形ABCD是正方形,N,E分别为AD,AB的中点,
∴DN=EB
∵BF平分∠CBM,AN=AE,∴∠DNE=∠EBF=90°+45°=135°
∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF
∴△DNE≌△EBF
∴
DE=EF,NE=BF
⑵在DA边上截取DN=EB(或截取AN=AE),连结NE,点N就使得NE=BF成立(图略)
此时,
DE=EF.
【学习目标】
1、
通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质.
2、通过具体实例认识中心对称,探索它的基本性质,理解对应点所连线段被对称中心平分的性质,了解平行四边形、圆是中心对称图形.
3、
能够按要求作出简单平面图形旋转后的图形,欣赏旋转在现实生活中的应用.
4、探索图形之间的变化关系(轴对称、平移、旋转及其组合),灵活运用轴对称、平移和旋转的组合进行图案设计.
【知识网络】
【巩固练习】
一、选择题
1.在下列四个图案中,既是轴对称图形,又是中心对称图形的是(
).
2.
时钟钟面上的分针从12时开始绕中心旋转120°,则下列说法正确的是( ).
A.此时分针指向的数字为3 B.此时分针指向的数字为6
C.此时分针指向的数字为4 D.分针转动3,但时针却未改变
3.如图,若正方形EFGH由正方形ABCD绕某点旋转得到,则可以作为旋转中心的是( ).
A.M或O或N
B.E或O或C
C.E或O或N
D.M或O或C
4.如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O顺时针旋转75°至OA′B′C′的位置,若OB=,∠C=120°,则点B′的坐标为( ).
A.(3,)
B.(3,)
C.(,)
D.(,)
第3题
第4题
第5题
5.如图,在Rt△ABC
中,∠ACB=90°,∠A=30°,BC=2.将△ABC绕点C按顺时针方向旋转n度后得到△EDC,此时点D在AB边上,斜边DE交AC边于点F,则n的大小和图中阴影部分的面积分别为( ).
A.30,2
B.60,2
C.60,
D.60,
6.
(2019 乌鲁木齐)如图,将斜边长为4的直角三角板放在直角坐标系xOy中,两条直角边分别与坐标轴重合,P为斜边的中点.现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是( )
A.(,1)
B.
(1,﹣)
C.
(2,﹣2)
D.
(2,﹣2)
7.
下列图案都是在一个图案的基础上,在“几何画板”软件中拖动一点后形成的,它们的共性是都可以由一个“基本图案”通过连续旋转得来,旋转的角度是( ).
A.30°
B.45°
C.60°
D.90°
8.在平面直角坐标系中,将点A1(6,1)向左平移4个单位到达点A2的位置,再向上平移3个单位到达点A3的位置,△A1A2A3绕点A2逆时针方向旋转900,则旋转后A3的坐标为(
).
A.(-2,1)
B.(1,1)
C.(-1,1)
D.(5,1)
二.
填空题
9.
(2019 扬州)如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=4,将△ABC绕直角顶点C顺时针旋转90°得到△DEC.若点F是DE的中点,连接AF,则AF= .
10.如图,正方形ABCD的边长为4cm,正方形AEFG的边长为1cm.如果正方形AEFG绕点A旋转,那么C、F两点之间的最小距离为 _________ cm.
11.绕一定点旋转180°后与原来图形重合的图形是中心对称图形,正六边形就是这样的图形.小明发现将正六边形绕着它的中心旋转一个小于180°的角,也可以使它与原来的正六边形重合,请你写出小明发现的一个旋转角的度数:_____________________.
12.如图所示,在Rt△ABC中,∠A=90°,AB=AC=4cm,以斜边BC上距离B点 cm的H为中心,把这个三角形按逆时针方向旋转90°至△DEF,则旋转前后两个直角三角形重叠部分的面积是___cm2.
13.如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,将腰CD以D为中心逆时针旋转90°至ED,连接AE、DE,△ADE的面积为3,则BC的长为_________.
14.
如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP绕点A逆时针旋转后与△ACP′重合,如果AP=3,那么线段PP′的长等于________.
15.如图,在直角坐标系中,已知点P0的坐标为(1,0),进行如下操作:将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2,如此重复操作下去,得到线段OP3,OP4,…,则:
(1)点P5的坐标为__________;
(2)落在x轴正半轴上的点Pn坐标是_________,其中n满足的条件是________.
16.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是__________.
三
综合题
17.
如图,已知,点P是正方ABCD内一点,且AP∶BP∶CP=1∶2∶3.
求证:∠APB=135°.
18.如图,已知点D是△ABC的BC边的中点,E、F分别是AB、AC上的点,且DE⊥DF.
求证:
BE
+
CF>EF
19.
(2019 黄冈中学自主招生)阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
请你回答:AP的最大值是
.
参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,则AP+BP+CP的最小值是
.(结果可以不化简)
20.如图14―1,14―2,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.
⑴如图14―1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是
;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是
;
③请证明你的上述两猜想.
⑵如图14―2,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系.
【答案与解析】
一、选择题
1.【答案】C.
2.【答案】C.
【解析】分针每5分钟转动30.
3.【答案】A.
【解析】
因为以M或O或N为旋转中心两个图形能够完全重合.
4.【答案】D.
【解析】因为是菱形,所以可得为等腰直角三角形.
5.【答案】C.
【解析】△BDC为正三角形,所以△FDC为直角三角形,∠DCF=30°,DF=1,FC=,即求得.
6.【答案】B.
【解析】根据题意画出△AOB绕着O点顺时针旋转120°得到的△COD,连接OP,OQ,过Q作QM⊥y轴,
∴∠POQ=120°,
∵AP=OP,
∴∠BAO=∠POA=30°,
∴∠MOQ=30°,
在Rt△OMQ中,OQ=OP=2,
∴MQ=1,OM=,
则P的对应点Q的坐标为(1,﹣),故选B
7.【答案】D.
8.【答案】C.
【解析】即旋转90°后坐标为(-1,1).
二、填空题
9.【答案】5.
【解析】作FG⊥AC,
根据旋转的性质,EC=BC=4,DC=AC=6,∠ACD=∠ACB=90°,
∵点F是DE的中点,
∴FG∥CD
∴GF=CD=AC=3
EG=EC=BC=2
∵AC=6,EC=BC=4
∴AE=2
∴AG=4
根据勾股定理,AF=5.
10.【答案】;
【解析】当点F在正方形ABCD的对角线AC上时,CF=AC﹣AF,当点F不在正方形的对角线上时由三角形的三边关系可知AC﹣AF<CF<AC+AF,
∴当点F在正方形ABCD的对角线AC上时,C、F两点之间的距离最小,
∴CF=AC﹣AF=4﹣=cm.
故答案为:.
11.【答案】60°或120°.
【解析】正六边形的中心角是60°.
12.【答案】1.
【解析】证明△FHC和△FHG是等腰直角三角形,且腰长为,即得.
13.【答案】5.
【解析】做DF⊥BC,EG⊥AD,交AD的延长线于点G
,则AD=BF,
可证得△DEG≌△DCF,即EG=FC,又因为,所以EG=3,
即BC=BF+FC=AD+EG=5.
14.【答案】.
【解析】由旋转可知△APP′是等腰直角三角形,所以PP′=.
15.【答案】(1)
,
(2)落在x轴正半轴上的点Pn坐标是,其中n满足的条件是n=8k(k=0,1,2,…)
16.【答案】(-1,).
【解析】首先求得的坐标,即可求得坐标.
三.解答题
17.【解析】证明:将△APB绕点B沿顺时针方向旋转90°至△CP′B
位置(如图),
则有△APB≌△CP′B.
∴BP′=
BP,CP′=AP,
∠PBP′=
90°,∠APB=∠CP′B.
设CP′=
AP=
k,则BP′=
BP=2k,CP=
3k,在Rt△BP′P中,
BP′=
BP=
2k,∴∠BP′P=45°.
=(3k)2=
CP2,
∴∠CP′P=90°,
∴∠CP′B=∠CP′P+∠BP′P=90°+45°=135°,
即∠APB=135°.
18.【解析】证明:将△BDE绕点D沿顺时针方向旋转180°至△CDG位置,则有△BDE≌△CDG.
∴BE=CG,ED=DG.
∵DE⊥DF,即
DF⊥EG.
∴EF=FG,在△FCG中CG+CF>FG,
即BE+CF>EF.
19.【解析】解:(1)如图2,∵△ABP逆时针旋转60°得到△A′BC,
∴∠A′BA=60°,A′B=AB,AP=A′C
∴△A′BA是等边三角形,
∴A′A=AB=BA′=2,
在△AA′C中,A′C<AA′+AC,即AP<6,
则当点A′A、C三点共线时,A′C=AA′+AC,即AP=6,即AP的最大值是:6;
故答案是:6.
(2)如图3,∵Rt△ABC是等腰三角形,∴AB=BC.
以B为中心,将△APB逆时针旋转60°得到△A'P'B.则A'B=AB=BC=4,PA=P′A′,PB=P′B,
∴PA+PB+PC=P′A′+P'B+PC.
∵当A'、P'、P、C四点共线时,(P'A+P'B+PC)最短,即线段A'C最短,
∴A'C=PA+PB+PC,
∴A'C长度即为所求.
过A'作A'D⊥CB延长线于D.
∵∠A'BA=60°(由旋转可知),
∴∠1=30°.
∵A'B=4,
∴A'D=2,BD=2,
∴CD=4+2.
在Rt△A'DC中A'C====2+2;
∴AP+BP+CP的最小值是:2+2(或不化简为).
故答案是:2+2(或不化简为).
20.【解析】
⑴ ①DE=EF;
②NE=BF.
③证明:
∵四边形ABCD是正方形,N,E分别为AD,AB的中点,
∴DN=EB
∵BF平分∠CBM,AN=AE,∴∠DNE=∠EBF=90°+45°=135°
∵∠NDE+∠DEA=90°,∠BEF+∠DEA=90°,∴∠NDE=∠BEF
∴△DNE≌△EBF
∴
DE=EF,NE=BF
⑵在DA边上截取DN=EB(或截取AN=AE),连结NE,点N就使得NE=BF成立(图略)
此时,
DE=EF.
同课章节目录
