人教版九年级数学上册教学讲义,复习补习资料(巩固练习):36【提高】弧、弦、圆心角、圆周角含答案
文档属性
| 名称 | 人教版九年级数学上册教学讲义,复习补习资料(巩固练习):36【提高】弧、弦、圆心角、圆周角含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 201.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 21:29:49 | ||
图片预览


文档简介
弧、弦、圆心角、圆周角—知识讲解(提高)
【学习目标】
1.了解圆心角、圆周角的概念;
2.理解圆周角定理及其推论,能灵活运用圆周角的定理及其推理解决有关问题;
3.掌握在同圆或等圆中,三组量:两个圆心角、两条弦、两条弧,只要有一组量相等,就可以推出其它两组量对应相等,及其它们在解题中的应用.
【巩固练习】
一、选择题
1.
如图,在⊙O中,若圆心角∠AOB=100°,C是上一点,则∠ACB等于(
).
A.80°
B.100°
C.130°
D.140°
2.已知,如图,
AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°。给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC。其中正确的有(
)个
A.
5
B.
4
C.
3
D.
2
第1题图
第2题图
第3题图
3.如图,设⊙O的半径为r,弦的长为a,弦与圆心的距离为d,弦的中点到所对劣弧中点的距离为h,下面说法或等式:①
②
③已知r、a、d、h中任意两个,可求其它两个。其中正确结论的序号是(
)
A.仅①
B.②③
C.①②③
D.①③
4.(2019 威海)如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
A.68°
B.
88°
C.
90°
D.112°
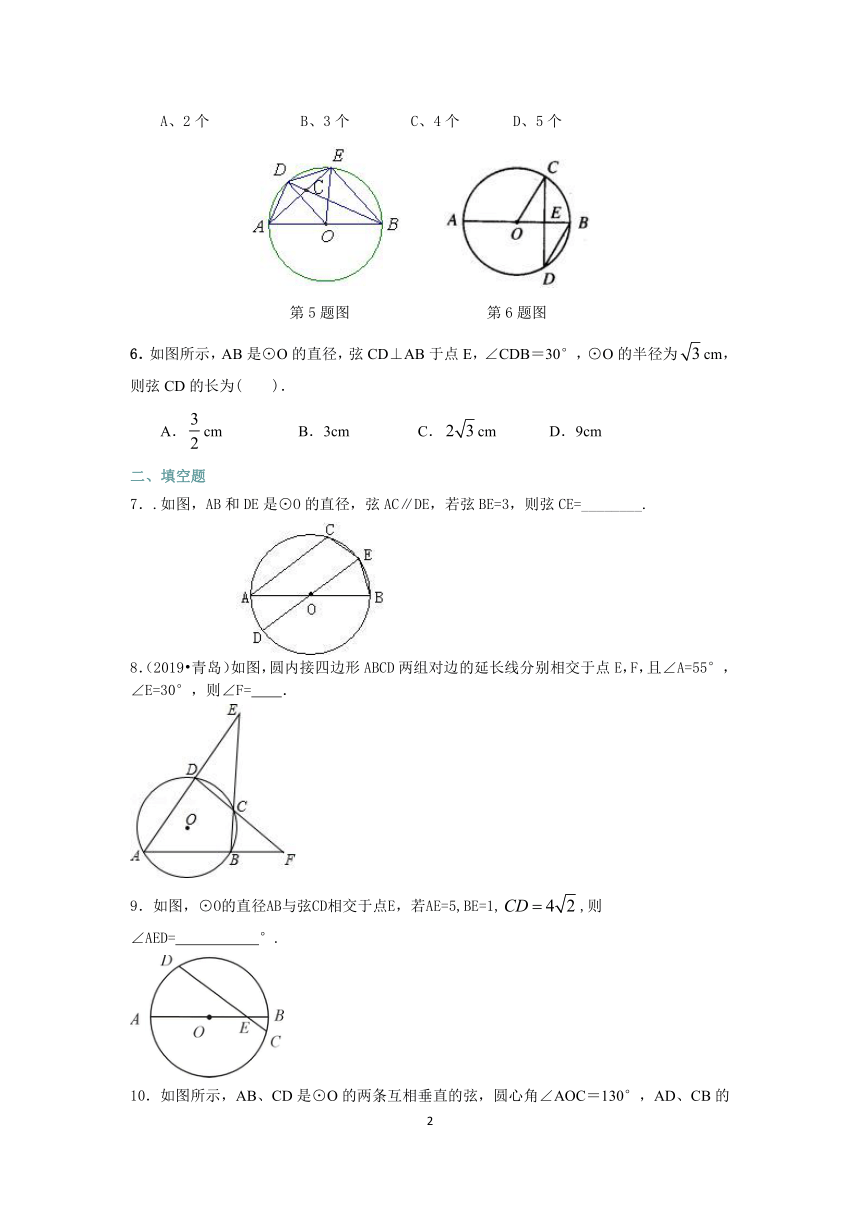
5.如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有(
)
A、2个
B、3个
C、4个
D、5个
第5题图
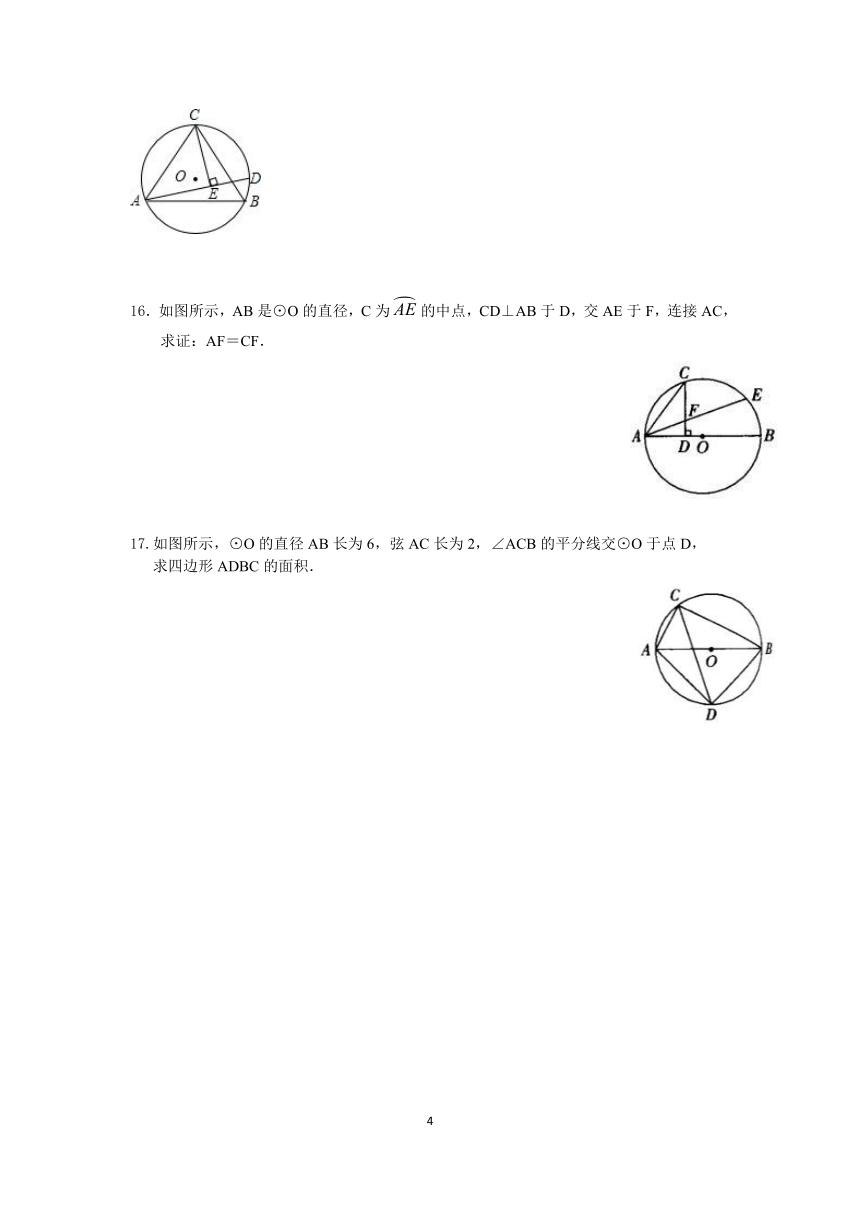
第6题图
6.如图所示,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD的长为(
).
A.cm
B.3cm
C.cm
D.9cm
二、填空题
7..如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.
8.(2019 青岛)如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F= .
9.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,BE=1,,则∠AED=
°.
10.如图所示,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD、CB的延长线相交于P,则∠P=________°.
11.如图所示,在半径为3的⊙O中,点B是劣弧的中点,连接AB并延长到D,使BD=AB,连接AC、BC、CD,如果AB=2,那么CD=________.
(第10题图)
(第11题图)
12.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,点B为中点,P直径MN上的一个动点,则PA+PB的最小值是
.
13.已知⊙O的半径OA=2,弦AB、AC分别为一元二次方程x2-(2+2)x+4=0的两个根,
则∠BAC的度数为_______.
三、解答题
14.如图,在⊙O中,,OB,OC分别交AC,BD于E、F,求证
15.(2019 宁波模拟)如图,等腰△ABC中,AC=BC,⊙O为△ABC的外接圆,D为上一点,CE⊥AD于E,求证:AE=BD+DE.
16.如图所示,AB是⊙O的直径,C为的中点,CD⊥AB于D,交AE于F,连接AC,
求证:AF=CF.
17.如图所示,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,
求四边形ADBC的面积.
【答案与解析】
一、选择题
1.【答案】C.
【解析】设点D是优弧AB上一点(不与A、B重合),连接AD、BD;
则∠ADB=∠AOB=50°;
∵四边形ADBC内接于⊙O,
∴∠C=180°-∠ADB=130°;故选C.
2.【答案】C.
【解析】①②④正确.
3.【答案】C.
【解析】根据垂径定理及勾股定理可得①②③都是正确的.
4.【答案】B.
【解析】如图,∵AB=AC=AD,
∴点B、C、D在以点A为圆心,
以AB的长为半径的圆上;
∵∠CBD=2∠BDC,
∠CAD=2∠CBD,∠BAC=2∠BDC,
∴∠CAD=2∠BAC,而∠BAC=44°,
∴∠CAD=88°,
故选B.
5.【答案】D.
【解析】与∠BCE相等的角有5个,∠DAE=∠AED=∠ABD,∠BAD=∠BAE+∠DAE=∠BAE+∠ABD=∠BCE,
同理∠ADO=∠ODE=∠OED=∠BCE,且∠ACD=∠BCE.
6.【答案】B.
【解析】∵
∠CDB=30°,
∴
∠COB=2∠CDB=60°,
又AB为⊙O的直径,CD⊥AB,
∴
∠OCD=30°,,
在Rt△OEC中,∵
cm,∴
cm.
(cm).
∴
cm,∴
CD=3cm.
二、填空题
7.【答案】3;
8.【答案】40°;
【解析】∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
9.【答案】30°;
10.【答案】40°;
【解析】∵
∠AOC=130°,
∴
∠ADC=∠ABC=65°,
又AB⊥CD,
∴
∠PCD=90°-65°=25°,
∴
∠P=∠ADC-∠PCD=65°-25°=40°.
11.【答案】;
【解析】连结OA、OB,交AC于E,因为点B是劣弧的中点,所以
OB⊥AC,设BE=x,则OE=3-x,由AB2-BE2=OA2-OE2得
22-x2=32-(3-x)2,解得,.
或连接OA、OB,△OAB∽△BCD,,,.
12.【答案】;
【解析】作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.(如图)
此时PA+PB最小,且等于AC的长.
连接OA,OC,根据题意得弧AN的度数是60°,
则弧BN的度数是30°,
根据垂径定理得弧CN的度数是30°,
则∠AOC=90°,又OA=OC=1,
则AC=
.
13.【答案】15°或75°.
【解析】方程x2-(2+2)x+4=0的解为x1=2,x2=2,
不妨设:AB=2,AC=2.
(1)如图,OM⊥AB于M,ON⊥AC于N.
∵AB=2,AC=2,
∴AM=,
∵OA=2,在Rt△MAO中,∠MAO=45°,AC=2,
∴AN=,
在Rt△NAO中,∠NAO=30°,∴∠BAC=15°;
(2)如图,∠BAC=75°.
三、解答题
14.【答案与解析】
如图,∵,∴,
∴,∵B,C是的中点,
∴,
∴,
∴
15.【答案与解析】
证明:如图,在AE上截取AF=BD,连接CF,CD;
在△ACF和△BCD中
∴△ACF≌△BCD,
∴CF=CD,
∵CE⊥AD于E,
∴EF=DE,
∴AE=AF+EF=BD+DE.
16.【答案与解析】
证法一:连接BC,如图所示.
∵
AB是直径,∴
∠ACB=90°,
即∠ACF+∠BCD=90°.
又∵
CD⊥AB,
∴
∠B+∠BCD=90°,
∴
∠ACF=∠B.
∵
点C是的中点,
∴
,
∴
∠B=∠CAE,
∴
∠ACF=∠CAE,∴
AF=CF.
证法二:如图所示,连接BC,并延长CD交⊙O于点H.
∵
AB是直径,CD⊥AB,
∴
.
∴
点C是的中点,
∴
,
∴
.
∵
∠ACF=∠CAF,
∴
AF=CF.
17.【答案与解析】
∵
AB是直径,∴
∠ACB=∠ADB=∠90°.
在Rt△ABC中,AB=6,AC=2,
∴
.
∵
∠ACB的平分线交⊙O于点D,∴
∠DCA=∠BCD.
∴
,∴
AD=BD.
∴
在Rt△ABD中,AD2+BD2=AB2=62,∴
AD=BD=.
∴
.
2
【学习目标】
1.了解圆心角、圆周角的概念;
2.理解圆周角定理及其推论,能灵活运用圆周角的定理及其推理解决有关问题;
3.掌握在同圆或等圆中,三组量:两个圆心角、两条弦、两条弧,只要有一组量相等,就可以推出其它两组量对应相等,及其它们在解题中的应用.
【巩固练习】
一、选择题
1.
如图,在⊙O中,若圆心角∠AOB=100°,C是上一点,则∠ACB等于(
).
A.80°
B.100°
C.130°
D.140°
2.已知,如图,
AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°。给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧是劣弧的2倍;⑤AE=BC。其中正确的有(
)个
A.
5
B.
4
C.
3
D.
2
第1题图
第2题图
第3题图
3.如图,设⊙O的半径为r,弦的长为a,弦与圆心的距离为d,弦的中点到所对劣弧中点的距离为h,下面说法或等式:①
②
③已知r、a、d、h中任意两个,可求其它两个。其中正确结论的序号是(
)
A.仅①
B.②③
C.①②③
D.①③
4.(2019 威海)如图,已知AB=AC=AD,∠CBD=2∠BDC,∠BAC=44°,则∠CAD的度数为( )
A.68°
B.
88°
C.
90°
D.112°
5.如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有(
)
A、2个
B、3个
C、4个
D、5个
第5题图
第6题图
6.如图所示,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为cm,则弦CD的长为(
).
A.cm
B.3cm
C.cm
D.9cm
二、填空题
7..如图,AB和DE是⊙O的直径,弦AC∥DE,若弦BE=3,则弦CE=________.
8.(2019 青岛)如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠A=55°,∠E=30°,则∠F= .
9.如图,⊙O的直径AB与弦CD相交于点E,若AE=5,BE=1,,则∠AED=
°.
10.如图所示,AB、CD是⊙O的两条互相垂直的弦,圆心角∠AOC=130°,AD、CB的延长线相交于P,则∠P=________°.
11.如图所示,在半径为3的⊙O中,点B是劣弧的中点,连接AB并延长到D,使BD=AB,连接AC、BC、CD,如果AB=2,那么CD=________.
(第10题图)
(第11题图)
12.如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,点B为中点,P直径MN上的一个动点,则PA+PB的最小值是
.
13.已知⊙O的半径OA=2,弦AB、AC分别为一元二次方程x2-(2+2)x+4=0的两个根,
则∠BAC的度数为_______.
三、解答题
14.如图,在⊙O中,,OB,OC分别交AC,BD于E、F,求证
15.(2019 宁波模拟)如图,等腰△ABC中,AC=BC,⊙O为△ABC的外接圆,D为上一点,CE⊥AD于E,求证:AE=BD+DE.
16.如图所示,AB是⊙O的直径,C为的中点,CD⊥AB于D,交AE于F,连接AC,
求证:AF=CF.
17.如图所示,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,
求四边形ADBC的面积.
【答案与解析】
一、选择题
1.【答案】C.
【解析】设点D是优弧AB上一点(不与A、B重合),连接AD、BD;
则∠ADB=∠AOB=50°;
∵四边形ADBC内接于⊙O,
∴∠C=180°-∠ADB=130°;故选C.
2.【答案】C.
【解析】①②④正确.
3.【答案】C.
【解析】根据垂径定理及勾股定理可得①②③都是正确的.
4.【答案】B.
【解析】如图,∵AB=AC=AD,
∴点B、C、D在以点A为圆心,
以AB的长为半径的圆上;
∵∠CBD=2∠BDC,
∠CAD=2∠CBD,∠BAC=2∠BDC,
∴∠CAD=2∠BAC,而∠BAC=44°,
∴∠CAD=88°,
故选B.
5.【答案】D.
【解析】与∠BCE相等的角有5个,∠DAE=∠AED=∠ABD,∠BAD=∠BAE+∠DAE=∠BAE+∠ABD=∠BCE,
同理∠ADO=∠ODE=∠OED=∠BCE,且∠ACD=∠BCE.
6.【答案】B.
【解析】∵
∠CDB=30°,
∴
∠COB=2∠CDB=60°,
又AB为⊙O的直径,CD⊥AB,
∴
∠OCD=30°,,
在Rt△OEC中,∵
cm,∴
cm.
(cm).
∴
cm,∴
CD=3cm.
二、填空题
7.【答案】3;
8.【答案】40°;
【解析】∵∠A=55°,∠E=30°,
∴∠EBF=∠A+∠E=85°,
∵∠A+∠BCD=180°,
∴∠BCD=180°﹣55°=125°,
∵∠BCD=∠F+∠CBF,
∴∠F=125°﹣85°=40°.
9.【答案】30°;
10.【答案】40°;
【解析】∵
∠AOC=130°,
∴
∠ADC=∠ABC=65°,
又AB⊥CD,
∴
∠PCD=90°-65°=25°,
∴
∠P=∠ADC-∠PCD=65°-25°=40°.
11.【答案】;
【解析】连结OA、OB,交AC于E,因为点B是劣弧的中点,所以
OB⊥AC,设BE=x,则OE=3-x,由AB2-BE2=OA2-OE2得
22-x2=32-(3-x)2,解得,.
或连接OA、OB,△OAB∽△BCD,,,.
12.【答案】;
【解析】作点B关于MN的对称点C,连接AC交MN于点P,则P点就是所求作的点.(如图)
此时PA+PB最小,且等于AC的长.
连接OA,OC,根据题意得弧AN的度数是60°,
则弧BN的度数是30°,
根据垂径定理得弧CN的度数是30°,
则∠AOC=90°,又OA=OC=1,
则AC=
.
13.【答案】15°或75°.
【解析】方程x2-(2+2)x+4=0的解为x1=2,x2=2,
不妨设:AB=2,AC=2.
(1)如图,OM⊥AB于M,ON⊥AC于N.
∵AB=2,AC=2,
∴AM=,
∵OA=2,在Rt△MAO中,∠MAO=45°,AC=2,
∴AN=,
在Rt△NAO中,∠NAO=30°,∴∠BAC=15°;
(2)如图,∠BAC=75°.
三、解答题
14.【答案与解析】
如图,∵,∴,
∴,∵B,C是的中点,
∴,
∴,
∴
15.【答案与解析】
证明:如图,在AE上截取AF=BD,连接CF,CD;
在△ACF和△BCD中
∴△ACF≌△BCD,
∴CF=CD,
∵CE⊥AD于E,
∴EF=DE,
∴AE=AF+EF=BD+DE.
16.【答案与解析】
证法一:连接BC,如图所示.
∵
AB是直径,∴
∠ACB=90°,
即∠ACF+∠BCD=90°.
又∵
CD⊥AB,
∴
∠B+∠BCD=90°,
∴
∠ACF=∠B.
∵
点C是的中点,
∴
,
∴
∠B=∠CAE,
∴
∠ACF=∠CAE,∴
AF=CF.
证法二:如图所示,连接BC,并延长CD交⊙O于点H.
∵
AB是直径,CD⊥AB,
∴
.
∴
点C是的中点,
∴
,
∴
.
∵
∠ACF=∠CAF,
∴
AF=CF.
17.【答案与解析】
∵
AB是直径,∴
∠ACB=∠ADB=∠90°.
在Rt△ABC中,AB=6,AC=2,
∴
.
∵
∠ACB的平分线交⊙O于点D,∴
∠DCA=∠BCD.
∴
,∴
AD=BD.
∴
在Rt△ABD中,AD2+BD2=AB2=62,∴
AD=BD=.
∴
.
2
同课章节目录
