北师大版数学八年级下册4.2提取公因式法(一)课件(共23张PPT)
文档属性
| 名称 | 北师大版数学八年级下册4.2提取公因式法(一)课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 465.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-25 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
4.2 提取公因式法
回顾与思考
1.多项式的分解因式的概念:
把一个多项式__________________的
形式,叫做把这个多项式分解因式.
2.分解因式与整式乘法是_____过程.
3.分解因式要注意以下几点:
① 分解的对象必须是_______.
② 分解的结果一定是几个整式的_____的形式.
化为几个整式乘积
互逆
多项式
乘积
练习一 理解概念
判断下列各式哪些是整式乘法?哪些是因式分解?
(1) x2-4y2=(x+2y)(x-2y);
(2) 2x(x-3y)=2x2-6xy
(3) (5a-1)2=25a2-10a+1 ;
(4) x2+4x+4=(x+2)2 ;
(5) (a-3)(a+3)=a2-9
(6) m2-4=(m+2)(m-2) ;
(7) 2πR+ 2πr= 2π(R+r).
因式分解
整式乘法
整式乘法
因式分解
整式乘法
因式分解
因式分解
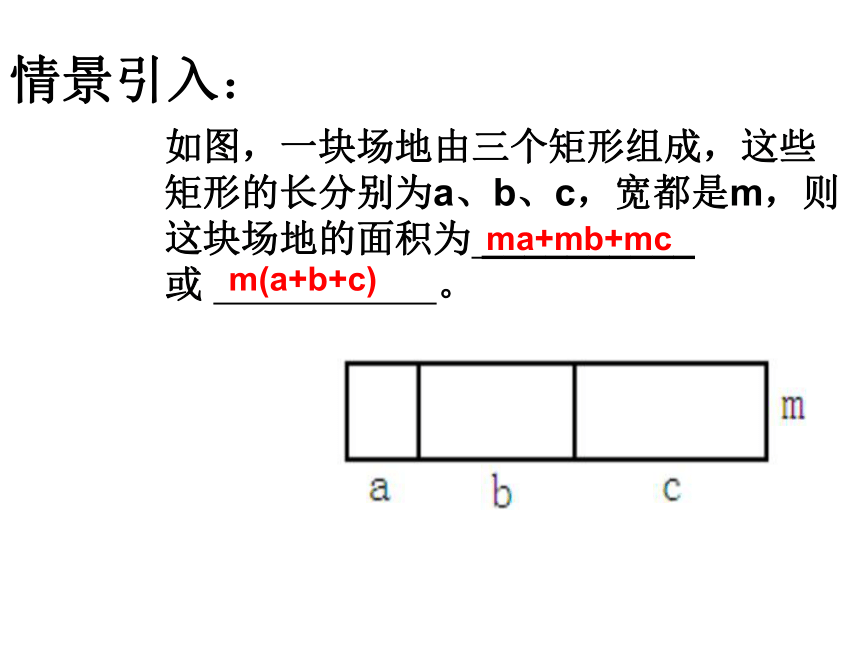
情景引入:
如图,一块场地由三个矩形组成,这些矩形的长分别为a、b、c,宽都是m,则这块场地的面积为 __________ 或 。
ma+mb+mc
m(a+b+c)
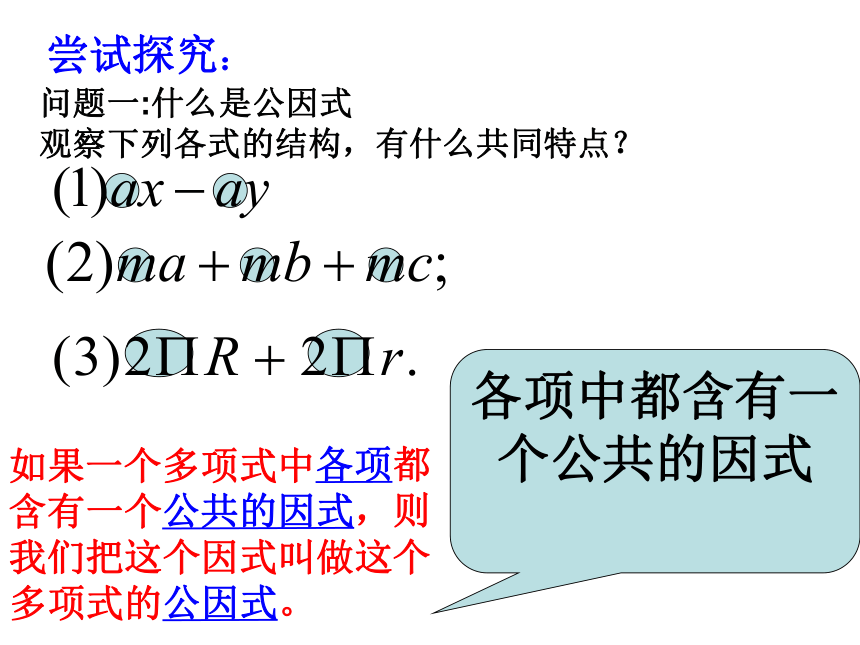
问题一:什么是公因式
观察下列各式的结构,有什么共同特点?
各项中都含有一个公共的因式
如果一个多项式中各项都含有一个公共的因式,则我们把这个因式叫做这个多项式的公因式。
尝试探究:
怎样确定多项式的公因式?
想一想:
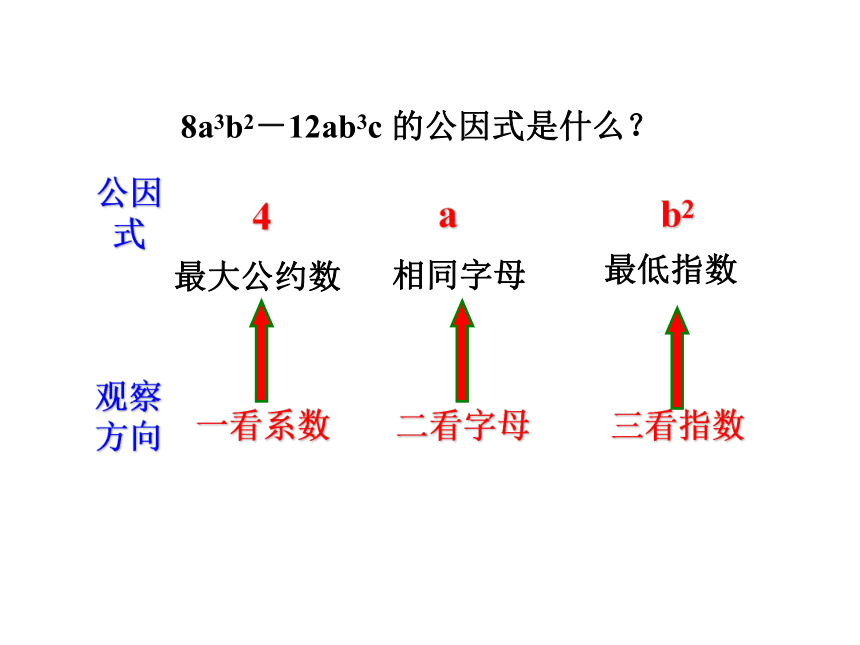
8a3b2-12ab3c 的公因式是什么?
最大公约数
相同字母
公因式
4
a
b2
一看系数
观察方向
二看字母
三看指数
最低指数
多项式中各项都含有的相同因式,叫做这个多项式各项的公因式。
系数:找各项的最大公约数。
字母:找各项的相同字母
指数:找相同字母的最低次幂
多项式的公因式
如何确定公因式?
注意:各项系数都是整数时,因式的系数应取各项系数的最大公约数;字母取各项的相同的字母,而且各字母的指数取次数最低的.
说出下列多项式各项的公因式:
(1)ma + mb ;
(2)4kx- 8ky ;
(3)5y3+20y2 ;
(4)a2b-2ab2+ab .
m
4k
5y2
ab
回顾:
如果多项式的各项有公因式,那么可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法,叫做提取公因式。
3、提公因式法分解因式步骤(分两步):
第一步,找出公因式;
第二步,提公因式
4、用提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)提公因式后某一项剩下因式“1”不能漏写;
(3)多项式的首项取正号.
例1 (1)把8a3b2 + 12ab3c 分解因式.
解:8a3b2+12ab3c
=4ab2?2a2+4ab2?3bc
=4ab2(2a2+3bc).
提公因式后,另一个因式:
①项数应与原多项式的项数一样;
②不再含有公因式.
例1 (2) 把12a4b3+16a2b3c2分解因式.
解:12a4b3+16a2b3c2
=4a2b3·3a2+ 4a2b3 ·4c2
= 4a2b3 (3a2 + 4c2)
公因式: 4a2b3
课堂练习
1.用提取公因式法分解因式。
1要留守家门
想一想:
用提公因式法分解因式与单项式乘多项式有什么关系?
例题2 把下列各式分解因式
解:(1)8x-72=8(x-9);
(2)a2b-5ab=ab(a-5);
(3)4m3-6m2=2m2(2m-3);
(4)a2b-5ab+9b=b(a2-5a+9);
例题3:
注意:当多项式第一项的系数是负数时,通常先提出“-”号,使括号内第一项的系数成为正数.在提出“-”号时,多项式的各项都要变号.
课堂练习:
2.写出下列多项式各项的公因式:
(1)xy-x (2)
(3) (4)
3.把下列各式分解因式:
(1) (2)
解:(1)x ;(2)4y3 ; (3)b ; (4)2ab
解:(1)3a2-9ab=3a(a-3b);
(2)-2x-8x3+4×2=-2(x+4x3-4).
课堂练习
4.把下列各式分解因式:
解:(1)-a2+ab-ac=-(a2-ab+ac)=-a(a-b+c);
(2)-2x3+6x2-2x=-(2x3-6x2+2x)=-2x(x2-3x+1).
课堂练习
5.利用分解因式进行计算
(1)3.14×77+3.14×32-3.14×9;
(2)121×0.13+12.1×0.9-12×1.21.
解:(1)3.14×77+3.14×32-3.14×9
=3.14×(77+32-9)
=3.14×100
=314.
(2)121×0.13+12.1×0.9-12×1.21
=12.1×1.3+12.1×0.9-12.1×1.2
=12.1×(1.3+0.9-1.2)
=12.1×1
=12.1.
课堂小结:
学习本节课后,你有哪些收获和感悟?你还有什么疑问?与同伴交流。
回顾小结:
提公因式法的依据,是分配律:
提公因式法的关键,是找出各相关的公因式:
提公因式法的步骤:
(1)确定公因式:
(2)确定与公因式相乘的另一个因式。
课后练习
1.利用因式分解进行计算: 1.47×18+1.47×43+39×1.47
2.小刚同学这样做因式分解:
你同意他的做法吗?若不同意,请你帮小刚同学改正。
解:1.47×18+1.47×43+39×1.47
=1.47×(18+43+39)
=1.47×100=147.
解:不同意. 3x2-6xy+x=x(3x-6y+1).
再见!
4.2 提取公因式法
回顾与思考
1.多项式的分解因式的概念:
把一个多项式__________________的
形式,叫做把这个多项式分解因式.
2.分解因式与整式乘法是_____过程.
3.分解因式要注意以下几点:
① 分解的对象必须是_______.
② 分解的结果一定是几个整式的_____的形式.
化为几个整式乘积
互逆
多项式
乘积
练习一 理解概念
判断下列各式哪些是整式乘法?哪些是因式分解?
(1) x2-4y2=(x+2y)(x-2y);
(2) 2x(x-3y)=2x2-6xy
(3) (5a-1)2=25a2-10a+1 ;
(4) x2+4x+4=(x+2)2 ;
(5) (a-3)(a+3)=a2-9
(6) m2-4=(m+2)(m-2) ;
(7) 2πR+ 2πr= 2π(R+r).
因式分解
整式乘法
整式乘法
因式分解
整式乘法
因式分解
因式分解
情景引入:
如图,一块场地由三个矩形组成,这些矩形的长分别为a、b、c,宽都是m,则这块场地的面积为 __________ 或 。
ma+mb+mc
m(a+b+c)
问题一:什么是公因式
观察下列各式的结构,有什么共同特点?
各项中都含有一个公共的因式
如果一个多项式中各项都含有一个公共的因式,则我们把这个因式叫做这个多项式的公因式。
尝试探究:
怎样确定多项式的公因式?
想一想:
8a3b2-12ab3c 的公因式是什么?
最大公约数
相同字母
公因式
4
a
b2
一看系数
观察方向
二看字母
三看指数
最低指数
多项式中各项都含有的相同因式,叫做这个多项式各项的公因式。
系数:找各项的最大公约数。
字母:找各项的相同字母
指数:找相同字母的最低次幂
多项式的公因式
如何确定公因式?
注意:各项系数都是整数时,因式的系数应取各项系数的最大公约数;字母取各项的相同的字母,而且各字母的指数取次数最低的.
说出下列多项式各项的公因式:
(1)ma + mb ;
(2)4kx- 8ky ;
(3)5y3+20y2 ;
(4)a2b-2ab2+ab .
m
4k
5y2
ab
回顾:
如果多项式的各项有公因式,那么可以把这个公因式提到括号外面,将多项式写成因式乘积的形式,这种分解因式的方法,叫做提取公因式。
3、提公因式法分解因式步骤(分两步):
第一步,找出公因式;
第二步,提公因式
4、用提公因式法分解因式应注意的问题:
(1)公因式要提尽;
(2)提公因式后某一项剩下因式“1”不能漏写;
(3)多项式的首项取正号.
例1 (1)把8a3b2 + 12ab3c 分解因式.
解:8a3b2+12ab3c
=4ab2?2a2+4ab2?3bc
=4ab2(2a2+3bc).
提公因式后,另一个因式:
①项数应与原多项式的项数一样;
②不再含有公因式.
例1 (2) 把12a4b3+16a2b3c2分解因式.
解:12a4b3+16a2b3c2
=4a2b3·3a2+ 4a2b3 ·4c2
= 4a2b3 (3a2 + 4c2)
公因式: 4a2b3
课堂练习
1.用提取公因式法分解因式。
1要留守家门
想一想:
用提公因式法分解因式与单项式乘多项式有什么关系?
例题2 把下列各式分解因式
解:(1)8x-72=8(x-9);
(2)a2b-5ab=ab(a-5);
(3)4m3-6m2=2m2(2m-3);
(4)a2b-5ab+9b=b(a2-5a+9);
例题3:
注意:当多项式第一项的系数是负数时,通常先提出“-”号,使括号内第一项的系数成为正数.在提出“-”号时,多项式的各项都要变号.
课堂练习:
2.写出下列多项式各项的公因式:
(1)xy-x (2)
(3) (4)
3.把下列各式分解因式:
(1) (2)
解:(1)x ;(2)4y3 ; (3)b ; (4)2ab
解:(1)3a2-9ab=3a(a-3b);
(2)-2x-8x3+4×2=-2(x+4x3-4).
课堂练习
4.把下列各式分解因式:
解:(1)-a2+ab-ac=-(a2-ab+ac)=-a(a-b+c);
(2)-2x3+6x2-2x=-(2x3-6x2+2x)=-2x(x2-3x+1).
课堂练习
5.利用分解因式进行计算
(1)3.14×77+3.14×32-3.14×9;
(2)121×0.13+12.1×0.9-12×1.21.
解:(1)3.14×77+3.14×32-3.14×9
=3.14×(77+32-9)
=3.14×100
=314.
(2)121×0.13+12.1×0.9-12×1.21
=12.1×1.3+12.1×0.9-12.1×1.2
=12.1×(1.3+0.9-1.2)
=12.1×1
=12.1.
课堂小结:
学习本节课后,你有哪些收获和感悟?你还有什么疑问?与同伴交流。
回顾小结:
提公因式法的依据,是分配律:
提公因式法的关键,是找出各相关的公因式:
提公因式法的步骤:
(1)确定公因式:
(2)确定与公因式相乘的另一个因式。
课后练习
1.利用因式分解进行计算: 1.47×18+1.47×43+39×1.47
2.小刚同学这样做因式分解:
你同意他的做法吗?若不同意,请你帮小刚同学改正。
解:1.47×18+1.47×43+39×1.47
=1.47×(18+43+39)
=1.47×100=147.
解:不同意. 3x2-6xy+x=x(3x-6y+1).
再见!
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
