安徽省蒙城庄子中学联盟2019--2020学年度第一学期九年级第三次月考数学试卷(含解析)
文档属性
| 名称 | 安徽省蒙城庄子中学联盟2019--2020学年度第一学期九年级第三次月考数学试卷(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 358.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-25 00:00:00 | ||
图片预览



文档简介
蒙城庄子中学联盟九年级第三次月考数学试卷
(满分150分 考试时间120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1. 二次函数的图象向右平移3个单位,得到新的图象的函数表达式是( )
A. B. C. D.
2. 如图,一个小球由地面沿着坡度i=1:2的坡面向上前进了10m,此时小球距离地面的高度为( )
A. 5m B. m C. m D. m
3. 已知二次函数有最小值1,则的大小关系为( )
A. B. C. D. 不能确定
4. 下列交通标志中既是中心对称图形,又是轴对称图形的是( )
5、如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )
A. = B. =
C. = D. =
第5题 第6题 第7题
6、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=2,BD=1,则AD的长是( )
A. 1 B. C. 2 D. 4
7、如图,在△ABC中,AB=AC=13,BC=10,点D为BC的中点,DE⊥AB于点E,则tan∠BDE的值等于( )
A. B. C. D.
8、在一个可以改变容积的密闭容器内,装有一定质量m的某种气体,当改变容积V时,气体的密度p也随之改变,ρ与V在一定范围内满足ρ=,它的图象如图所示,则该气体的质量m为( )
1.4kg B. 5kg C. 7kg D. ?6.4kg
9、如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P、Q两点,则函数y=ax2+(b-1)x+c的图象可能为( )
10.已知二次函数y=ax2+bx+c(a≠0)的图像如图所示,并且关于x的一元二次方程ax2+bx+c –m=0有两个实数根,下列结论:①b2-4ac>0;②abc>0;③;④,其中正确的个数有( )
A. 1 B. 2 C. 3 D. 4
二、填空题(本大题共5小题,每小题4分,满分20分)
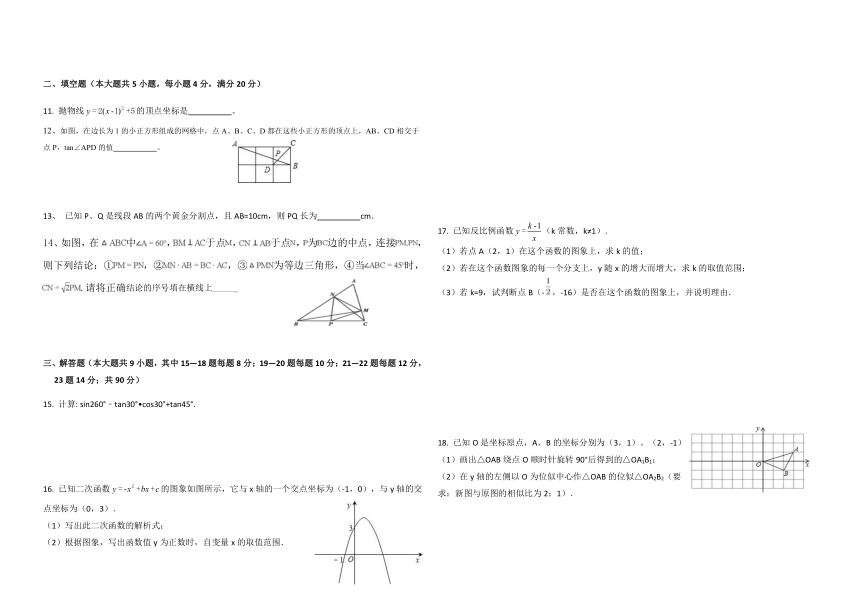
11. 抛物线的顶点坐标是 。
12、如图,在边长为1的小正方形组成的网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点P,tan∠APD的值 。
13、 已知P、Q是线段AB的两个黄金分割点,且AB=10cm,则PQ长为 cm.
14、如图,在中,于点,于点,为边的中点,连接,则下列结论:①,②,③为等边三角形,④当时,.请将正确结论的序号填在横线上______
三、解答题(本大题共9小题,其中15—18题每题8分;19—20题每题10分;21—22题每题12分,23题14分;共90分)
15. 计算: sin260°﹣tan30°?cos30°+tan45°.
16. 已知二次函数的图象如图所示,它与x轴的一个交点坐标为(-1,0),与y轴的交点坐标为(0,3).
(1)写出此二次函数的解析式;
(2)根据图象,写出函数值y为正数时,自变量x的取值范围.
17. 已知反比例函数(k常数,k≠1).
(1)若点A(2,1)在这个函数的图象上,求k的值;
(2)若在这个函数图象的每一个分支上,y随x的增大而增大,求k的取值范围;
(3)若k=9,试判断点B(-,-16)是否在这个函数的图象上,并说明理由.
18. 已知O是坐标原点,A、B的坐标分别为(3,1)、(2,-1)
(1)画出△OAB绕点O顺时针旋转90°后得到的△OA1B1;
(2)在y轴的左侧以O为位似中心作△OAB的位似△OA2B2(要求:新图与原图的相似比为2:1).
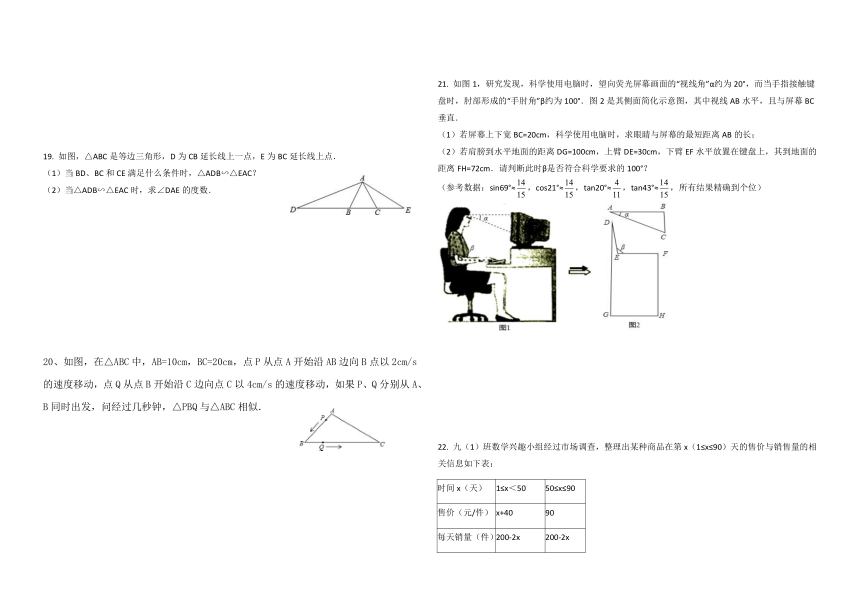
19. 如图,△ABC是等边三角形,D为CB延长线上一点,E为BC延长线上点.
(1)当BD、BC和CE满足什么条件时,△ADB∽△EAC?
(2)当△ADB∽△EAC时,求∠DAE的度数.
20、如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿AB边向B点以2cm/s的速度移动,点Q从点B开始沿C边向点C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,问经过几秒钟,△PBQ与△ABC相似.
21. 如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈,cos21°≈,tan20°≈,tan43°≈,所有结果精确到个位)
22. 九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200-2x 200-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
23. 已知:如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,AE⊥BD,EF⊥CE
(1)试证明△AEF∽△BEC;
(2)如图,过C点作CH⊥AD于H,试探究线段DH与BF的数量关系,并说明理由;
(3)若AD=1,CD=5,试求出BE的值?
蒙城庄子中学联盟九年级第三次月考数学试卷参考答案
(满分150分 考试时间120分钟)
一、选择题(本大题共10小题,每小题4分,满分40分)
1.
【解析】
解:原抛物线的顶点为(0,0),向右平移3个单位,那么新抛物线的顶点为(3,0).?
可设新抛物线的解析式为:,?
代入得:.?
故选:D.
2.
【解析】
【答案】D【知识点】勾股定理
3.
【解析】
解:∵二次函数y=a(x+1)2-b(a≠0)有最小值,?
∴抛物线开口方向向上,即a>0;?
又最小值为1,即-b=1,∴b=-1,?
∴a>b.?
故选:A.
4、
【解析】
选项A是轴对称图形但不是中心对称图形,选项B、C既不是中心对称图形也不是轴对称图形.只有选项D既是轴对称图形又是中心对称图形
5.
【解析】
解:∵∠A=∠A,∠ADE=∠B,∴△AED∽△ACB,∴.
故选B.
. 6、【解析】
解:∵∠ACB=90°,CD⊥AB于点D,∴∠ADC=∠CDB=90°,∠A+∠B=90°,∠B+∠BCD=90°,
∴∠A=∠BCD,∴△ADC∽△CDB,∴AD:CD=CD:BD,
∵CD=2,BD=1,∴AD=4.故选:D.
7、
【解析】
解:连接AD,
∵△ABC中,AB=AC=13,BC=10,D为BC中点,
∴AD⊥BC,BD=BC=5,
∴AD==12,
∴tan∠BAD==.
∵AD⊥BC,DE⊥AB,
∴∠BDE+∠ADE=90°,∠BAD+∠ADE=90°,
∴∠BDE=∠BAD,
∴tan∠BDE=tan∠BAD=.
故选:C.
8 【解析】
解:∵ρ=,∴m=ρV,而点(5,1.4)在图象上,
代入得m=5×1.4=7(kg).
故选C.
9、【解析】本题考查二次函数与一元二次方程的关系.根据一次函数y1=x与二次函数y2=ax2+bx+c图象在第一象限相交于P、Q两点,观察图象可知一元二次方程ax2+bx+c= x的根为两个正根,即关于x的一元二次方程ax2+bx+c-x=0有两个正实数根,故函数y=ax2+(b-1)x+c的图象与x轴交点的横坐标均为正数,
故选A.
10【答案】D
【解析】
轴交点个数以及抛物线与方程之间的关系、函数图象与各系数之间关系分析得出答案.
【详解】如图所示:图象与x轴有两个交点,则b2-4ac>0,故①正确;
∵图象开口向上,∴a>0, ∵对称轴在y轴右侧,∴a,b异号,∴b<0,∵图象与y轴交于x轴下方,
∴c<0,∴abc>0,故②正确;当x=-1时,a-b+c>0,故③正确;∵二次函数y=ax2+bx+c的顶点坐标纵坐标为:-2,
故二次函数y=ax2+bx+c向上平移不超过2个单位,则平移后解析式y=ax2+bx+c-m与x轴有交点,此时关于x的一元二次方程ax2+bx+c-m=0有两个实数根,故-m≤2,解得:m≥-2,故④正确.故选:D.
二、填空题(本大题共5小题,每小题4分,满分20分)
11.【解析】
解:根据二次函数的性质可得抛物线y=2(x﹣1)2+5的顶点坐标是(1,5);
故答案为(1,5).
12、 分析:P点不在网格线的格点上,无法发挥网格线的作用,可以将∠APD转化为一个顶点在格点上的角,如何转化,利用网格线构造平行,从而得到相等的角。
解:如图,连接BE,AE。
∵DE∥BC DE=BC
∴四边形DEBC是平行四边形
∴DC∥BE
∴∠ABE=∠APD
由勾股定理得
BE=,AE=2,AB=
∵AB?=BE?+AE?
∴∠AEB=90°
∴tan∠APD= tan∠ABE==2.
13. 已知P、Q是线段AB的两个黄金分割点,且AB=10cm,则PQ长为 cm.
【解析】
解:如图,
由题意得,AQ=BP=cm,
∴PQ=AQ+BP-AB=cm.
故答案为.
此题考查了黄金分割的知识.注意掌握黄金分割点的定义是解此题的关键.首先根据题意画出图形,由P、Q是线段AB的两个黄金分割点,可求得AQ与BP的长,继而求得答案.
【答案】
14、【答案】①③④
【解析】
①根据直角三角形斜边上的中线等于斜边的一半可判断①;
②先证明△ABM∽△ACN,再根据相似三角形的对应边成比例可判断②;
③先根据直角三角形两锐角互余的性质求出∠ABM=∠ACN=30°,再根据三角形的内角和定理求出∠BCN+∠CBM=60°,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠BPN+∠CPM=120°,从而得到∠MPN=60°,又由①得PM=PN,根据有一个角是60°的等腰三角形是等边三角形可判断③;
④当∠ABC=45°时,∠BCN=45°,进而判断④.
【详解】①∵BM⊥AC于M,CN⊥AB于点N,P为BC边的中点,
∴PM=BC,PN=BC,点
∴PM=PN,正确;
②在△ABM与△ACN中,
∵∠A=∠A,∠AMB=∠ANC=90°,
∴△ABM∽△ACN,
∴,错误;
③∵∠A=60°,BM⊥AC于点M,CN⊥AB于点N,
∴∠ABM=∠ACN=30°,
在△ABC中,∠BCN+∠CBM=180°-60°-30°×2=60°,
∵点P是BC的中点,BM⊥AC,CN⊥AB,
∴PM=PN=PB=PC,
∴∠BPN=2∠BCN,∠CPM=2∠CBM,
∴∠BPN+∠CPM=2(∠BCN+∠CBM)=2×60°=120°,
∴∠MPN=60°,
∴△PMN是等边三角形,正确;
④当∠ABC=45°时,∵CN⊥AB于点N,
∴∠BNC=90°,∠BCN=45°,
∵P为BC中点,可得BC=PB=PC,故④正确.
所以正确的选项有:①③④
故答案为:①③④
三、解答题(本大题共9小题,其中15—18题每题8分;19—20题每题10分;21—22题每题12分,23题14分;共90分)
15、【解析】
解:原式=
=
=.
16、.【解析】
解:(1)根据题意得,
解得,
所以二次函数解析式为y=-x2+2x+3;
(2)当y=0时,-x2+2x+3=0,
解得x1=-1,x2=3,
则抛物线与x轴的两交点坐标为(-1,0),(3,0),
所以当-1<x<3时,y>0.
(1)把(-1,0)和(0,3)分别代入y=-x2+bx+c中得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;?
(2)先求出抛物线与x轴的交点坐标,然后利用图象找出抛物线在x轴上方所对应的自变量的范围即可
17.【解析】
解:(1)把A(2,1)代入y=得k-1=2×1,解得k=3;
(2)根据题意得k-1<0,解得k<1;
(3)在.理由如下:
当k=9时,反比例函数解析式为y=,
因为-×(-16)=8,
所以点B在这个函数的图象上.
(1)根据反比例函数图象上点的坐标特征得到k-1=2×1,然后解方程即可;
(2)根据反比例函数的性质得k-1<0,然后解不等式;
(3)根据反比例好图象上点的坐标特征解析判断.
18、略、
19. 如图,
【解析】
解:(1)当BC2=BD?CE时,△ADB∽△EAC,
∵△ABC是等边三角形,
∴AB=BC=CA,∠ABC=∠ACB=60°,
∴∠ABD=∠ACE=120°,
∵BC2=BD?CE,
∴AB?AC=BD?CE,
∴,
∴△ADB∽△EAC;
(2)∵△ADB∽△EAC,
∴∠D=∠CAE,
∵∠ABC=∠D+∠DAB=60°,
∴∠CAE+∠DAB=60°,
∴∠DAE=∠CAE+∠DAB+∠BAC=60°+60°=120°.
(1)由等边三角形得AB=BC=CA、∠ABC=∠ACB=60°,即∠ABD=∠ACE=120°,结合BC2=BD?CE知AB?AC=BD?CE,据此可得答案;?
(2)由△ADB∽△EAC知∠D=∠CAE,由∠ABC=∠D+∠DAB=60°知∠CAE+∠DAB=60°,根据∠DAE=∠CAE+∠DAB+∠BAC可得答案.
本题主要考查相似三角形的判定与性质,解题的关键是熟练掌握相似三角形的判定及等边三角形的性质.
20、解答: 解:设经过秒后t秒后,△PBQ与△ABC相似,则有AP=2t,BQ=4t,BP=10﹣2t,当△PBQ∽△ABC时,有BP:AB=BQ:BC,即(10﹣2t):10=4t:20,解得t=2.5(s)(6分)当△QBP∽△ABC时,有BQ:AB=BP:BC,即4t:10=(10﹣2t):20,解得t=1.所以,经过2.5s或1s时,△PBQ与△ABC相似(10分).解法二:设ts后,△PBQ与△ABC相似,则有,AP=2t,BQ=4t,BP=10﹣2t分两种情况:(1)当BP与AB对应时,有=,即=,解得t=2.5s(2)当BP与BC对应时,有=,即=,解得t=1s所以经过1s或2.5s时,以P、B、Q三点为顶点的三角形与△ABC相似.
21、【解析】
解:(1)∵Rt△ABC中,tanA=,
∴AB====55(cm);
(2)延长FE交DG于点I.
则DI=DG-FH=100-72=28(cm).
在Rt△DEI中,sin∠DEI===,
∴∠DEI=69°,
∴∠β=180°-69°=111°≠100°,
∴此时β不是符合科学要求的100°.
(1)Rt△ABC中利用三角函数即可直接求解;?
(2)延长FE交DG于点I,利用三角函数求得∠DEI即可求得β的值,从而作出判断.
此题综合性比较强,解此题的关键是把实际问题转化为数学问题,本题只要把实际问题抽象到几何图形中来考虑,就能迎刃而解.
22. 【解析】
解:(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x+2000,
当50≤x≤90时,
y=(200-2x)(90-30)=-120x+12000,
综上所述:y=;
(2)当1≤x<50时,
y=-2x2+180x+2000,
y=-2(x-45)2+6050.
∴a=-2<0,
∴二次函数开口向下,二次函数对称轴为x=45,
当x=45时,y最大=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)①当1≤x<50时,y=-2x2+180x+2000≥4800,
解得:20≤x≤70,
因此利润不低于4800元的天数是20≤x<50,共30天;
②当50≤x≤90时,y=-120x+12000≥4800,
解得:x≤60,
因此利润不低于4800元的天数是50≤x≤60,共11天,
所以该商品在整个销售过程中,共41天每天销售利润不低于4800元.
(1)根据单价乘以数量,可得利润,可得答案;?
(2)根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案;?
(3)根据二次函数值大于或等于4800,一次函数值大于或等于48000,可得不等式,根据解不等式组,可得答案.,利用单价乘以数量求函数解析式,利用了函数的性质求最值.
23. 【解析】
(1)证明:∵AE⊥BD,EF⊥CE,
∴∠AEB=∠FEC=90°,
∴∠AEF=∠BEC,
∵∠ABC=90°,
∴∠ABE+∠EBC=90°,∠ABE+∠FAE=90°,
∴∠FAE=∠EBC,
∴△AEF∽△BEC;
(2)解:结论:DH=BF.
理由:∵△AEF∽△BEC,
∴=,
∵∠ABE=∠ABD,∠AEB=∠BAD=90°,
∴△ABE∽△DBA,
∴=,
∴=,
?∵BC=AB,
∴AF=AD,
∵∠ABC=∠BAD=∠H=90°,
∴四边形ABCH是矩形,
∵AB=BC,
∴四边形ABCH是正方形,
∴AB=AH,∵AF=AD,
∴BF=DH.
(3)设正方形的边长为x,
在Rt△CDH中,DH=x-1,CH=x,CD=5,
∴52=x2+(x-1)2,
解得x=4,
∴AB=4,AD=1,
在Rt△ABD中,BD==,
∵?AD?AB=?BD?AE,
∴AE==,
在Rt△AEB中,BE==.
(1)想办法证明∠AEF=∠BEC,∠FAE=∠EBC即可解决问题;?
(2)结论:DH=BF.利用比例的性质首先证明AD=AF,再证明四边形ABCH是正方形即可解决问题;?
(3)设正方形的边长为x,在Rt△CDH中,DH=x-1,CH=x,CD=5,可得52=x2+(x-1)2,解得x=4,再通过解直角三角形求出BE的长即可;
本题考查相似三角形综合题、比例的性质、正方形的判定和性质、勾股定理等知识,解题的关键是学勾股定理会添加常用辅助线,构造特殊四边形解决问题,属于中考压轴题.
