湘教版九年级数学下册第2章圆:2.6弧长与扇形面积 (第1课时 弧长) 课件(共19张ppt)
文档属性
| 名称 | 湘教版九年级数学下册第2章圆:2.6弧长与扇形面积 (第1课时 弧长) 课件(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
第2章 圆
2.6 弧长
【学习目标】
1.理解并掌握弧长公式的推导过程,会运用弧长公式进
行计算.
2.经历弧长公式的推导过程,进一步培养学生探究问题
的能力.
【学习重点】
弧长公式及其运用.
【学习难点】
运用弧长公式解决实际问题.
教学目标
(1)已知⊙O的半径为R,⊙O的周长是多少?
(2)什么叫圆心角?
C=2πR
顶点在圆心,两边和圆相交所组成的角叫做圆心角.
温故知新:
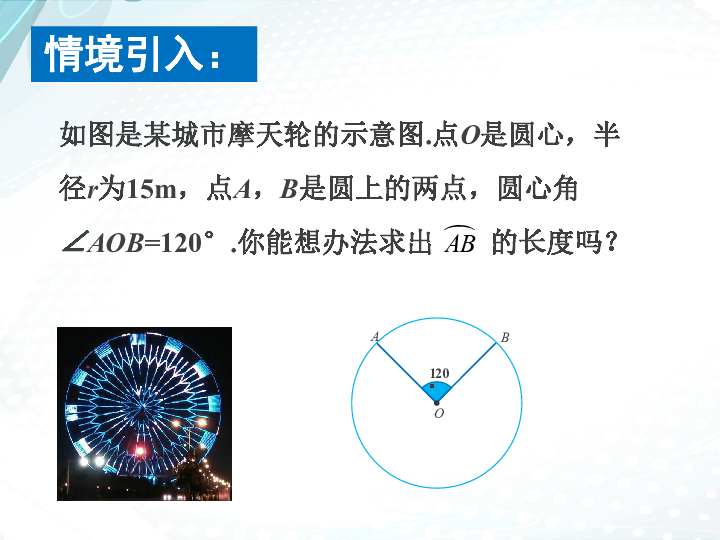
如图是某城市摩天轮的示意图.点O是圆心,半径r为15m,点A,B是圆上的两点,圆心角∠AOB=120°.你能想办法求出 的长度吗?
O
A
B
120°
情境引入:
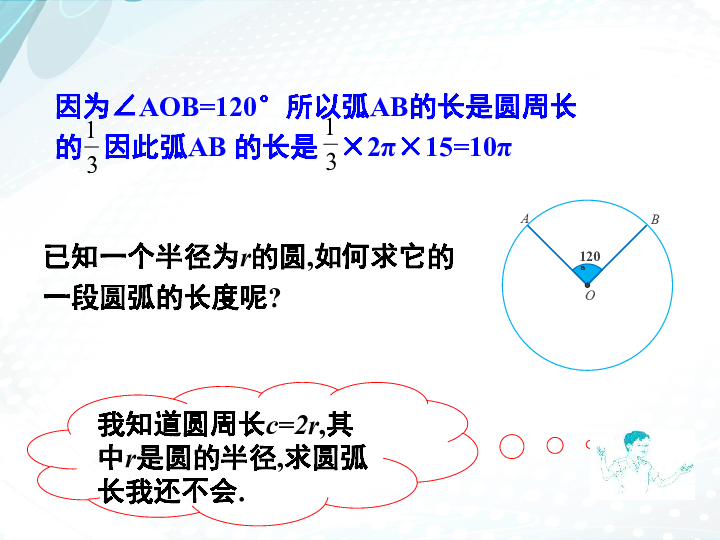
因为∠AOB=120°所以弧AB的长是圆周长的 因此弧AB 的长是 ×2π×15=10π
O
A
B
120°
已知一个半径为r的圆,如何求它的一段圆弧的长度呢?
我知道圆周长c=2r,其中r是圆的半径,求圆弧长我还不会.
阅读教材P77~P78,完成下列问题:
弧长公式是什么?如何推导?
自主学习:
(1)半径为R的圆,周长是多少?
C=2πR
(3)1°圆心角所对弧长是多少?
(4)140°圆心角所对的
弧长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
若设⊙O半径为R, n°的圆心角所对的弧长为l,则
n°
A
B
O
新知探究:
1.由于在同一个圆中,相等的圆心角所对的弧相等,因此:1°的圆心角所对弧长为
2.所以得出:n°的圆心角所对的弧长l为
半径为r的圆中,n°的圆心角所对的弧长l为:
R
·
n°
1°
O
归纳总结:
1、弧长与哪些因素有关?
2、在3个量l、R、n中,只要已知其中两个量就可以求第三个量,那么请将公式变形求出R和n。
思考:
l
A
B
O
n°
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
(1)在应用弧长公式 ,进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
温馨提示:
例1 已知圆O的半径为30cm,求40°的圆心角所对的弧长(精确到0.1cm)
解:
40°的圆心角所对的弧长20.9cm
n°
典例解析:
●
B
B1
B2
例2.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.
(1)1o的弧长是 ,半径为10厘米
的圆中,60o的圆心角所对的弧长是 .
(2)如图同心圆中,大圆半径OA、OB交小圆与C、D,且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )
O
A
B
C
D
A、1∶1 B、1∶2
C、2∶1 D、1∶4
B
随堂练习:
(3) 如图:在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC与B点,若OA=6,求弧AB的长。
A
C
B
O
课堂总结:
谈谈你的收获?
1.已知弧所对的圆心角为90 °,半径是4,则弧长为 。
2. 已知一条弧的半径为9,弧长为8π,那么这条弧所对的 圆心角为 。
3.已知一条弧的弧长为4π ,那么这条弧所对的圆周角为 45 ° ,这条弧所在的半径 。
4. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D.
2π
160 °
B
8
知识检测:
如图,直角三角形ABC的斜边AB=35,点O在AB边上,OB=20,一个以O为圆心的圆,分别切两直角边BC,AC于D、E两点,求 的长度.
直击中考:
连接OE、OD,
∵⊙O切BC、AC于点D、E,
∴OD⊥BC,OE⊥AC.
∵∠C=90°,
∴四边形OECD为矩形,
∠EOD=90°, OE=OD.
设⊙O的半径为r,即OE=OD=r.
∵∠A+∠B=90°,∠DOB+∠B=90°.
∴ ∠A=∠DOB.
又∵ ∠AEO=∠ODB=90°,
∴△AEO∽△ODB.
∴ , ∴ ,
∴ r =12,
∴ 的长度 =
第2章 圆
2.6 弧长
【学习目标】
1.理解并掌握弧长公式的推导过程,会运用弧长公式进
行计算.
2.经历弧长公式的推导过程,进一步培养学生探究问题
的能力.
【学习重点】
弧长公式及其运用.
【学习难点】
运用弧长公式解决实际问题.
教学目标
(1)已知⊙O的半径为R,⊙O的周长是多少?
(2)什么叫圆心角?
C=2πR
顶点在圆心,两边和圆相交所组成的角叫做圆心角.
温故知新:
如图是某城市摩天轮的示意图.点O是圆心,半径r为15m,点A,B是圆上的两点,圆心角∠AOB=120°.你能想办法求出 的长度吗?
O
A
B
120°
情境引入:
因为∠AOB=120°所以弧AB的长是圆周长的 因此弧AB 的长是 ×2π×15=10π
O
A
B
120°
已知一个半径为r的圆,如何求它的一段圆弧的长度呢?
我知道圆周长c=2r,其中r是圆的半径,求圆弧长我还不会.
阅读教材P77~P78,完成下列问题:
弧长公式是什么?如何推导?
自主学习:
(1)半径为R的圆,周长是多少?
C=2πR
(3)1°圆心角所对弧长是多少?
(4)140°圆心角所对的
弧长是多少?
(2)圆的周长可以看作是多少度的圆心角所对的弧?
若设⊙O半径为R, n°的圆心角所对的弧长为l,则
n°
A
B
O
新知探究:
1.由于在同一个圆中,相等的圆心角所对的弧相等,因此:1°的圆心角所对弧长为
2.所以得出:n°的圆心角所对的弧长l为
半径为r的圆中,n°的圆心角所对的弧长l为:
R
·
n°
1°
O
归纳总结:
1、弧长与哪些因素有关?
2、在3个量l、R、n中,只要已知其中两个量就可以求第三个量,那么请将公式变形求出R和n。
思考:
l
A
B
O
n°
(2)区分弧、弧的度数、弧长三概念.度数相等的弧,弧长不一定相等,弧长相等的弧也不一定是等孤,而只有在同圆或等圆中,才可能是等弧.
(1)在应用弧长公式 ,进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的;
温馨提示:
例1 已知圆O的半径为30cm,求40°的圆心角所对的弧长(精确到0.1cm)
解:
40°的圆心角所对的弧长20.9cm
n°
典例解析:
●
B
B1
B2
例2.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至B2结束所走过的路径长度________.
(1)1o的弧长是 ,半径为10厘米
的圆中,60o的圆心角所对的弧长是 .
(2)如图同心圆中,大圆半径OA、OB交小圆与C、D,且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )
O
A
B
C
D
A、1∶1 B、1∶2
C、2∶1 D、1∶4
B
随堂练习:
(3) 如图:在△AOC中,∠AOC=900,∠C=150,以O为圆心,AO为半径的圆交AC与B点,若OA=6,求弧AB的长。
A
C
B
O
课堂总结:
谈谈你的收获?
1.已知弧所对的圆心角为90 °,半径是4,则弧长为 。
2. 已知一条弧的半径为9,弧长为8π,那么这条弧所对的 圆心角为 。
3.已知一条弧的弧长为4π ,那么这条弧所对的圆周角为 45 ° ,这条弧所在的半径 。
4. 钟表的轴心到分针针端的长为5cm,那么经过40分钟,分针针端转过的弧长是( )
A. B. C. D.
2π
160 °
B
8
知识检测:
如图,直角三角形ABC的斜边AB=35,点O在AB边上,OB=20,一个以O为圆心的圆,分别切两直角边BC,AC于D、E两点,求 的长度.
直击中考:
连接OE、OD,
∵⊙O切BC、AC于点D、E,
∴OD⊥BC,OE⊥AC.
∵∠C=90°,
∴四边形OECD为矩形,
∠EOD=90°, OE=OD.
设⊙O的半径为r,即OE=OD=r.
∵∠A+∠B=90°,∠DOB+∠B=90°.
∴ ∠A=∠DOB.
又∵ ∠AEO=∠ODB=90°,
∴△AEO∽△ODB.
∴ , ∴ ,
∴ r =12,
∴ 的长度 =
