北师大版九年级下册第二章2.2二次函数图像与性质2 练习(含答案)
文档属性
| 名称 | 北师大版九年级下册第二章2.2二次函数图像与性质2 练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 200.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-29 00:00:00 | ||
图片预览



文档简介
堂测3
1.(3分)已知二次函数的图象如图所示,对称轴是,则下列结论中正确的是(? )
A. B. C. D.
2.(3分)如图,已知二次函数的图象如图所示,给出以下四个结论:①,②,③,④;其中正确的结论有(? )
A.1 个 B.2 个 C.3 个 D.4 个
3.(3分)如图是二次函数的图象,其对称轴为,下列结论:①;②;③;④若,是抛物线上两点,则,其中结论正确的是(? )
A.①② B.②③ C.②④ D.①③④
堂测4
1.(3分)已知函数,则当时,自变量的取值范围是( )
A.或 B. C.或 D.
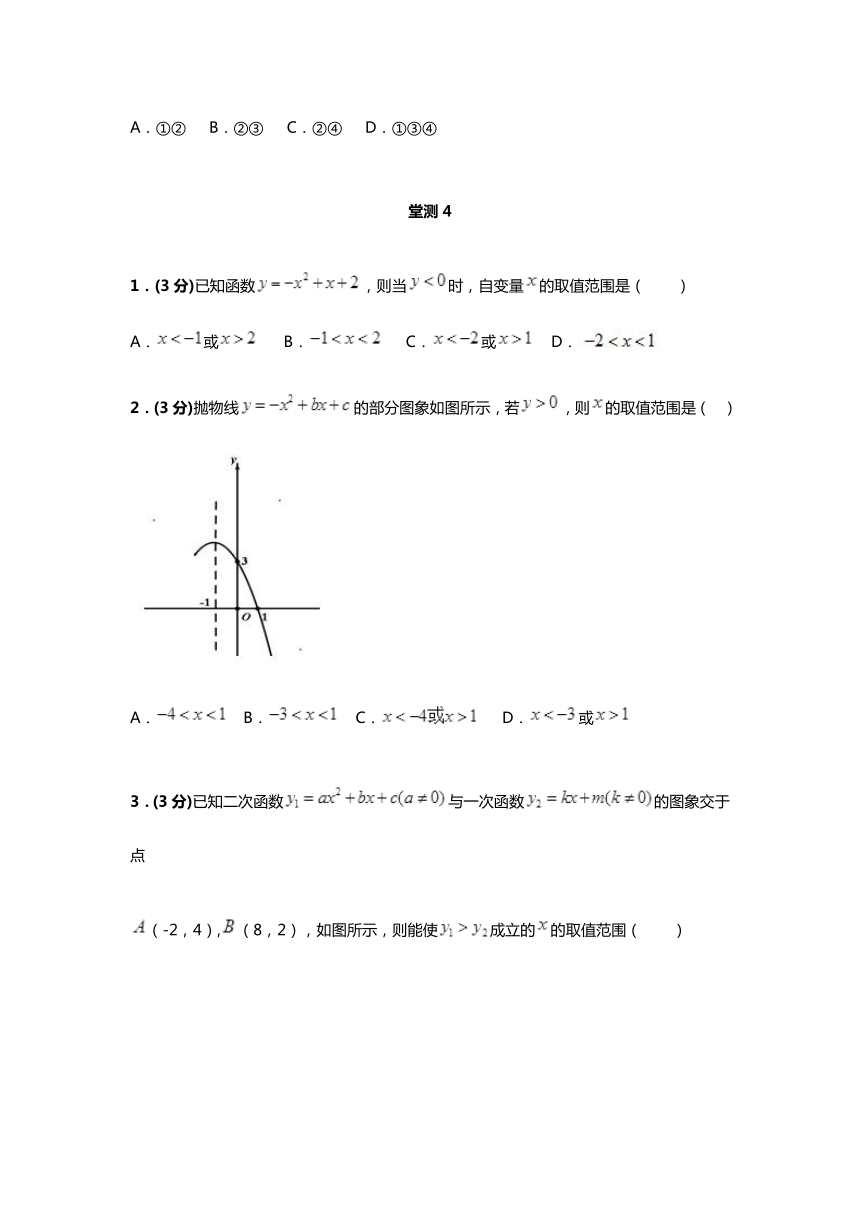
2.(3分)抛物线的部分图象如图所示,若,则的取值范围是(? )
A. B. C. D.或
3.(3分)已知二次函数与一次函数的图象交于点
(-2,4),(8,2),如图所示,则能使成立的的取值范围( )
A. B. C. D.或
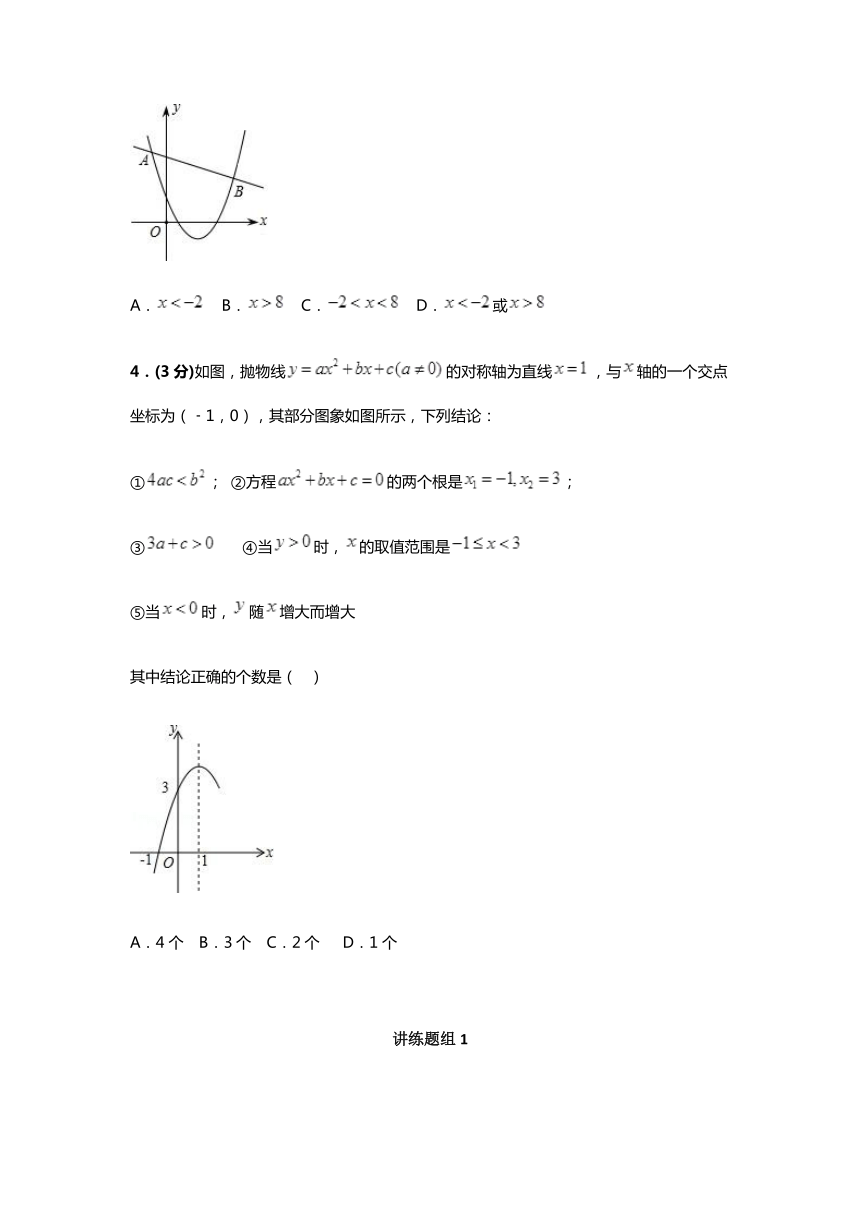
4.(3分)如图,抛物线的对称轴为直线,与轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①; ②方程的两个根是;
③???? ④当时,的取值范围是
⑤当时,随增大而增大
其中结论正确的个数是(? )
A.4个 B.3个 C.2个 D.1个
讲练题组1
1.(3分)已知二次函数的图象如图所示,下列结论:①,②,③,④;其中正确的个数是(?? )
A.1 B.2 C.3 D.4
2.(3分)已知二次函数的图象如图所示,对称轴为直线.有位学生写出了以下五个结论:
(1);? (2)方程的两根是;
(3);(4)当时,随的增大而减小;(5)
则以上结论中不正确的有(? )
A.1个 B.2个 C.3个 D.4个
3.(3分)已知二次函数的图象如图所示,有以下结论:①;②;③;④;⑤.其中所有正确结论的序号是(??? )
A.①② B.①③④ C.①②③⑤ D.①②③④⑤
4.(3分)如图,二次函数(a≠0)的图象与轴正半轴相交,其顶点坐标为(,1),下列结论:①;②;③;④.其中正确结论的个数是 (???)
A.1 B.2 C.3 D.4
5.(3分)已知二次函数的图象如图所示,有下列5个结论:
① ; ② ; ③ ;④ ;
⑤ ,(的实数)其中正确的结论有____________(填写序号).
6.(3分)如图所示:二次函数图象经过点(-1,2),且与轴交点的横坐标分别为,其中,,下列结论: ①;②;③;④其中正确的有(?? )
A.1个 B.2个 C.3个 D.4个
讲练题组2
1.(3分)抛物线与轴有两个不同的交点,则的取值范围为(??? )
A. B. C. D.
2.(3分)若二次函数的图象经过点(,0),则方程的解为(?? )
A., B., C., D.,
3.(3分)已知二次函数,当自变量取时,其相应的函数值小于,那么下列结论中正确的是(??? )
A.的函数值小于 B.的函数值大于 C.的函数值等于
D.的函数值与的大小关系不确定
4.(3分)下列关于二次函数()的图象与x轴交点的判断正确的是( )
A.没有交点 B.只有一个交点,且它位于y轴右侧
C.有两个交点,且它们均位于y轴左侧 D.有两个交点,且它们均位于y轴右侧
5.(3分)已知抛物线与轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与轴的交点在点(0,)的下方,那么的取值范围是( ???)
A. B. C. D.全体实数
6.(3分)若是关于的一元二次方程的两个根,且,则的大小关系是(?? )
A. B. C. D.
巩固作业
1.(3分)抛物线可以由抛物线平移得到,则下列平移过程正确的是(?? )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
2.(3分)将抛物线向左平移4个单位,再向上平移3个单位,得到抛物线的函数表达式是___________.
3.(3分)抛物线图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为,则的值为__________.
4.(3分)把二次函数的图象向左平移4个单位或向右平移1个单位后都会经过原点,则二次函数图象的对称轴与轴的交点坐标是( ?)
A.(-2.5, 0) B.(2.5, 0) C.(-1.5, 0) D.(1.5, 0)
5.(3分)已知二次函数(-1≤≤1),当从-1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线的移动方向的描述中,正确的是( )
A.先往左上方移动,再往左下方移动 B.先往左下方移动,再往左上方移动
C.先往右上方移动,再往右下方移动 D.先往右下方移动,再往右上方移动
6.(3分)将抛物线绕它的顶点旋转,所得抛物线的解析式是
A. B. C. D.
7.(3分)已知二次函数(是常数),把该函数的图象沿轴平移后,得到的函数图象与轴只有一个公共点,则应把该函数的图象
A.向上平移3个单位 B.向下平移3个单位 C.向上平移1个单位 D.向下平移1个单位
8.(6分)将抛物线向左平移4个单位,再向上平移3个单位,再绕点(1,2)旋转,求新抛物线的函数表达式.
9.(12分)如图,中,,点的坐标是,,以点为顶点的抛物线()经过轴上的点、.
⑴ 求点、、的坐标.
⑵ 求该抛物线分别关于轴、轴、原点、点(-1,1)对称的二次函数解析式.
⑶ 若抛物线向上平移后恰好经过点,求平移后抛物线的解析式.
堂测3答案与解析
1.(3分)
【考点】 二次函数位置与系数的关系
【答案】 D
2.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】 C
3.(3分)
【考点】 二次函数的图象和性质
【答案】 C
堂测4答案与解析
1.(3分)
【考点】 二次函数与一元二次方程
【答案】 A
2.(3分)
【考点】 二次函数的图象和性质
【答案】 B
3.(3分)
【考点】 二次函数与一元二次方程
【答案】 D
4.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系 二次函数与坐标轴的交点
【答案】 B
讲练题组1答案与解析
1.(3分)
【考点】 二次函数位置与系数的关系
【答案】 C
2.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】 B
3.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】 C
4.(3分)
【考点】 二次函数的图象和性质
【答案】 C
5.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】
③④⑤
6.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】 D
讲练题组2答案与解析
1.(3分)
【考点】 二次函数与坐标轴的交点
【答案】 A
2.(3分)
【考点】 二次函数与一元二次方程
【答案】 C
3.(3分)
【考点】 二次函数与坐标轴的交点
【答案】 B
4.(3分)
【考点】 二次函数与坐标轴的交点
【答案】 D
5.(3分)
【考点】 二次函数与坐标轴的交点
【答案】 A
6.(3分)
【考点】 二次函数与一元二次方程
【答案】 D
巩固作业答案与解析
1.(3分)
【考点】 二次函数图象变换
【答案】 B
2.(3分)
【考点】 二次函数解析式 二次函数图象变换
【答案】
3.(3分)
【考点】 二次函数解析式 二次函数图象变换
【答案】
4
4.(3分)
【考点】 二次函数图象变换
【答案】 D
5.(3分)
【考点】 二次函数图象变换
【答案】 C
6.(3分)
【考点】 二次函数解析式 二次函数图象变换
【答案】 D
7.(3分)
【考点】 二次函数图象变换
【答案】 B
8.(6分)
【考点】 二次函数解析式 二次函数图象变换
【答案】
9.(12分)
【考点】 二次函数解析式 二次函数图象变换 二次函数与坐标轴的交点
【答案】
(1);
(2),,,,
(3)
1.(3分)已知二次函数的图象如图所示,对称轴是,则下列结论中正确的是(? )
A. B. C. D.
2.(3分)如图,已知二次函数的图象如图所示,给出以下四个结论:①,②,③,④;其中正确的结论有(? )
A.1 个 B.2 个 C.3 个 D.4 个
3.(3分)如图是二次函数的图象,其对称轴为,下列结论:①;②;③;④若,是抛物线上两点,则,其中结论正确的是(? )
A.①② B.②③ C.②④ D.①③④
堂测4
1.(3分)已知函数,则当时,自变量的取值范围是( )
A.或 B. C.或 D.
2.(3分)抛物线的部分图象如图所示,若,则的取值范围是(? )
A. B. C. D.或
3.(3分)已知二次函数与一次函数的图象交于点
(-2,4),(8,2),如图所示,则能使成立的的取值范围( )
A. B. C. D.或
4.(3分)如图,抛物线的对称轴为直线,与轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①; ②方程的两个根是;
③???? ④当时,的取值范围是
⑤当时,随增大而增大
其中结论正确的个数是(? )
A.4个 B.3个 C.2个 D.1个
讲练题组1
1.(3分)已知二次函数的图象如图所示,下列结论:①,②,③,④;其中正确的个数是(?? )
A.1 B.2 C.3 D.4
2.(3分)已知二次函数的图象如图所示,对称轴为直线.有位学生写出了以下五个结论:
(1);? (2)方程的两根是;
(3);(4)当时,随的增大而减小;(5)
则以上结论中不正确的有(? )
A.1个 B.2个 C.3个 D.4个
3.(3分)已知二次函数的图象如图所示,有以下结论:①;②;③;④;⑤.其中所有正确结论的序号是(??? )
A.①② B.①③④ C.①②③⑤ D.①②③④⑤
4.(3分)如图,二次函数(a≠0)的图象与轴正半轴相交,其顶点坐标为(,1),下列结论:①;②;③;④.其中正确结论的个数是 (???)
A.1 B.2 C.3 D.4
5.(3分)已知二次函数的图象如图所示,有下列5个结论:
① ; ② ; ③ ;④ ;
⑤ ,(的实数)其中正确的结论有____________(填写序号).
6.(3分)如图所示:二次函数图象经过点(-1,2),且与轴交点的横坐标分别为,其中,,下列结论: ①;②;③;④其中正确的有(?? )
A.1个 B.2个 C.3个 D.4个
讲练题组2
1.(3分)抛物线与轴有两个不同的交点,则的取值范围为(??? )
A. B. C. D.
2.(3分)若二次函数的图象经过点(,0),则方程的解为(?? )
A., B., C., D.,
3.(3分)已知二次函数,当自变量取时,其相应的函数值小于,那么下列结论中正确的是(??? )
A.的函数值小于 B.的函数值大于 C.的函数值等于
D.的函数值与的大小关系不确定
4.(3分)下列关于二次函数()的图象与x轴交点的判断正确的是( )
A.没有交点 B.只有一个交点,且它位于y轴右侧
C.有两个交点,且它们均位于y轴左侧 D.有两个交点,且它们均位于y轴右侧
5.(3分)已知抛物线与轴交于两点,如果有一个交点的横坐标大于2,另一个交点的横坐标小于2,并且抛物线与轴的交点在点(0,)的下方,那么的取值范围是( ???)
A. B. C. D.全体实数
6.(3分)若是关于的一元二次方程的两个根,且,则的大小关系是(?? )
A. B. C. D.
巩固作业
1.(3分)抛物线可以由抛物线平移得到,则下列平移过程正确的是(?? )
A.先向左平移2个单位,再向上平移3个单位
B.先向左平移2个单位,再向下平移3个单位
C.先向右平移2个单位,再向下平移3个单位
D.先向右平移2个单位,再向上平移3个单位
2.(3分)将抛物线向左平移4个单位,再向上平移3个单位,得到抛物线的函数表达式是___________.
3.(3分)抛物线图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为,则的值为__________.
4.(3分)把二次函数的图象向左平移4个单位或向右平移1个单位后都会经过原点,则二次函数图象的对称轴与轴的交点坐标是( ?)
A.(-2.5, 0) B.(2.5, 0) C.(-1.5, 0) D.(1.5, 0)
5.(3分)已知二次函数(-1≤≤1),当从-1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线的移动方向的描述中,正确的是( )
A.先往左上方移动,再往左下方移动 B.先往左下方移动,再往左上方移动
C.先往右上方移动,再往右下方移动 D.先往右下方移动,再往右上方移动
6.(3分)将抛物线绕它的顶点旋转,所得抛物线的解析式是
A. B. C. D.
7.(3分)已知二次函数(是常数),把该函数的图象沿轴平移后,得到的函数图象与轴只有一个公共点,则应把该函数的图象
A.向上平移3个单位 B.向下平移3个单位 C.向上平移1个单位 D.向下平移1个单位
8.(6分)将抛物线向左平移4个单位,再向上平移3个单位,再绕点(1,2)旋转,求新抛物线的函数表达式.
9.(12分)如图,中,,点的坐标是,,以点为顶点的抛物线()经过轴上的点、.
⑴ 求点、、的坐标.
⑵ 求该抛物线分别关于轴、轴、原点、点(-1,1)对称的二次函数解析式.
⑶ 若抛物线向上平移后恰好经过点,求平移后抛物线的解析式.
堂测3答案与解析
1.(3分)
【考点】 二次函数位置与系数的关系
【答案】 D
2.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】 C
3.(3分)
【考点】 二次函数的图象和性质
【答案】 C
堂测4答案与解析
1.(3分)
【考点】 二次函数与一元二次方程
【答案】 A
2.(3分)
【考点】 二次函数的图象和性质
【答案】 B
3.(3分)
【考点】 二次函数与一元二次方程
【答案】 D
4.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系 二次函数与坐标轴的交点
【答案】 B
讲练题组1答案与解析
1.(3分)
【考点】 二次函数位置与系数的关系
【答案】 C
2.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】 B
3.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】 C
4.(3分)
【考点】 二次函数的图象和性质
【答案】 C
5.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】
③④⑤
6.(3分)
【考点】 二次函数的图象和性质 二次函数位置与系数的关系
【答案】 D
讲练题组2答案与解析
1.(3分)
【考点】 二次函数与坐标轴的交点
【答案】 A
2.(3分)
【考点】 二次函数与一元二次方程
【答案】 C
3.(3分)
【考点】 二次函数与坐标轴的交点
【答案】 B
4.(3分)
【考点】 二次函数与坐标轴的交点
【答案】 D
5.(3分)
【考点】 二次函数与坐标轴的交点
【答案】 A
6.(3分)
【考点】 二次函数与一元二次方程
【答案】 D
巩固作业答案与解析
1.(3分)
【考点】 二次函数图象变换
【答案】 B
2.(3分)
【考点】 二次函数解析式 二次函数图象变换
【答案】
3.(3分)
【考点】 二次函数解析式 二次函数图象变换
【答案】
4
4.(3分)
【考点】 二次函数图象变换
【答案】 D
5.(3分)
【考点】 二次函数图象变换
【答案】 C
6.(3分)
【考点】 二次函数解析式 二次函数图象变换
【答案】 D
7.(3分)
【考点】 二次函数图象变换
【答案】 B
8.(6分)
【考点】 二次函数解析式 二次函数图象变换
【答案】
9.(12分)
【考点】 二次函数解析式 二次函数图象变换 二次函数与坐标轴的交点
【答案】
(1);
(2),,,,
(3)
