人教版七年级上数学课件1.2.3相反数 (共33张PPT)
文档属性
| 名称 | 人教版七年级上数学课件1.2.3相反数 (共33张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 383.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 07:51:17 | ||
图片预览










文档简介
(共33张PPT)
1.2.3 相 反 数
1.掌握相反数的概念,理解它所包含的两种含义.(重点)
2.会求一个数的相反数,理解互为相反数的两个数在数轴上的位置关系.(重点、难点)
3.理解和掌握双重符号的化简规律.(重点)
相反数的定义
1.在数轴上,与原点的距离是6的点有两个,所表示的数分别
为__和___.
2.在数轴上,与原点的距离是10的点有两个,所表示的数分
别为___和____.
6
-6
10
-10
【思考】 1.观察上面两个题中你所填的两组数,各组数有什么
特点?
提示:每组数中的两个数只有符号不同.
2.表示各组数的点在数轴上的位置有什么特点?
提示:与原点的距离相等且分别在原点左右(即关于原点对称).
【总结】 1.相反数的定义:
(1)代数定义:只有_____不同的两个数叫做互为相反数,0的相
反数是__.
(2)几何定义:一般地,设a是一个正数,数轴上与原点的距离
是a的点有___个,它们分别在原点左右,表示-a和a,我们说这
两点关于原点_____,这里-a与a互为相反数.
符号
两
对称
0
2.求一个数的相反数的方法:只改变它的_____,其他部分都
_____.
3.多重符号的化简方法:因为一个数的前面加上“+”号等于
它的_____,一个数的前面加上“-”号等于它的_______,所以
把多重符号化为单一的符号时,如果是正号,可以_________,
如果是负号,取其_______即可.
符号
不变
本身
相反数
省略不写
相反数
(打“√”或“×”)
(1)符号不同的两个数互为相反数.( )
(2)-6的相反数是6.( )
(3)0没有相反数.( )
(4)a的相反数一定是负数.( )
(5)在数轴上离原点4个单位长度的点表示的数是4.( )
(6)在数轴上,表示互为相反数的两个点一定位于原点的两
侧.( )
×
√
×
×
×
×
1 相反数
【例1】分别写出2, , ,-2.5的相反数,并在数轴上标出
各数及它们的相反数,说明各对数在数轴上的位置特点.
【思路点拨】在所求数的前面添上“-”号,即得原数的相反
数→在数轴上表示出各数→观察各对数在数轴上的位置→结论
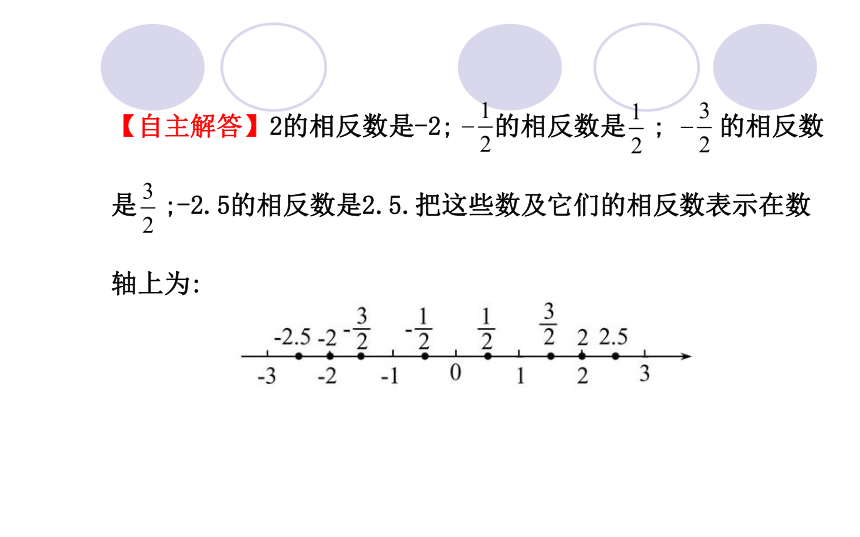
【自主解答】2的相反数是-2; 的相反数是 ; 的相反数
是 ;-2.5的相反数是2.5.把这些数及它们的相反数表示在数
轴上为:
2和-2, 和 , 和 ,-2.5和2.5,各对数在数轴上分别位
于原点两侧,且到原点的距离相等,即在数轴上表示每对数的
点关于原点对称.
【总结提升】求相反数的方法
1.在原数的前面加“-”号后,再进行符号化简.
2.复杂的数在求相反数前,可先进行符号化简,然后再变号.
2 多重符号的化简
【例2】(1)化简下列各数:
-(+5),-[-(+5)],-{-[-(+5)]}.
(2)猜想:当+5前面有2 013个正号时,化简的结果为______;
当+5前面有2 013个负号时,化简的结果为______;当+5前面
有2 012个负号时,化简的结果为______.
【解题探究】(1)-(+5)表示的意义是+5的_______,所以
-(+5)=___;
-[-(+5)]表示的意义是-(+5)的_______,而
-(+5)=___,所以-[-(+5)]=__;
-{-[-(+5)]}表示的意义是-[-(+5)]的_______,而
-[-(+5)]=__,所以-{-[-(+5)]}=_____.
相反数
-5
相反数
5
相反数
-5
-5
5
(2)①当+5前面只有“+”时,化简的结果的符号怎样?结果是
多少?
②当+5前面有奇数个“-”号时,化简的结果的符号怎样?结
果是多少?
③当+5前面有偶数个“-”号时,化简的结果的符号怎样?结
果是多少?
提示:①为正,5 ②为负,-5 ③为正,5
(3)由探究(2)的结论,能得出例2(2)的猜想吗?
提示:+5 -5 +5
【互动探究】化简数的符号时,结果的符号只与哪种符号有
关?
提示:化简数的符号时,结果的符号与“+”号无关,只与
“-”号的个数有关.当“-”号有偶数个时结果为正;当
“-”号有奇数个时结果为负.
【总结提升】多重符号化简的三个规律
1.把所有的正号去掉.
2.负号的个数是偶数时结果为正数,负号的个数为奇数时结果为负数,简称“奇负偶正”.
3.也可以采用两个同号得正,两个异号得负,分层化简的办法.
注意:多重符号的结果由“-”号的个数决定,与“+”号无关,最后结果的“+”号一般省略不写.
题组一:相反数
1.-7的相反数是( )
A.-7 B.7 C. D.
【解析】选B.与-7只有符号不同的数是7.
2.一个数的相反数是非负数,这个数一定是( )
A.正数或零 B.非零的数
C.负数或零 D.零
【解析】选C.正数的相反数是负数,0的相反数是0,即非负数
的相反数是非正数,即负数或零.
3.如果a=-a,那么表示a的点在数轴上的位置是在( )
A.原点左侧 B.原点右侧
C.原点上或原点右侧 D.原点上
【解析】选D.a=-a表示a与它的相反数-a相等,因为只有0的
相反数等于它本身,故a=0.
4.请你写出一对互为相反数的两个数:________与________.
【解析】只有符号不同的两个数互为相反数,因此写出只有符
号不同的两个数即可.
答案:2 -2(答案不唯一)
数a的相反数
数a的相反数是-a,这里的a是任意有理数,即a可以是正数、负数或0.
(1)当a>0时,-a<0(正数的相反数是负数).
(2)当a<0时,-a>0(负数的相反数是正数).
(3)当a=0时,-a=0(0的相反数是0).
综上可知,a不一定是正数,-a不一定是负数.
5.写出下列各数的相反数:
9,-0.3,-2 .
【解析】9的相反数是-9;-0.3的相反数是0.3;
-2 的相反数是2 .
6.已知m,n互为相反数,求6(m+n)- +2 012的值.
【解析】因为m,n互为相反数,所以m+n=0,所以
6(m+n)- +2 012=0-0+2 012=2 012.
题组二:多重符号的化简
1. 计算-(-5)等于( )
A.5 B.-5
C. D.-
【解析】选A.因为-(-5)表示-5的相反数,
所以-(-5)=5.
2.下列各数:+(-1),-[+(-3)],-(- ),-(-m),+[-(+ )]
其中正数有( )
A.1个 B.2个
C.3个 D.4个
【解析】选B.+(-1)=-1,-[+(-3)]=3,-(- )= ,
+[-(+ )]=- ,-(-m)=m,但m可能是正数,可能是负数,
也可能是0.
3.化简:-(-2 012)=______.
【解析】因为-(-2 012)表示-2 012的相反数,所以
-(-2 012)=2 012.
答案:2 012
4.-(+6)是 的相反数.
【解析】-(+6)=-6,是6的相反数.
答案:6
5.化简下列各数:
(1)-(+7).(2)+(-3).
(3)+(+ ).(4)-[-(- )].
【解析】(1)-(+7)=-7.
(2)+(-3)=-3.
(3)+(+ )= .
(4)-[-(- )]=- .
【归纳整合】多重符号的化简方法
(1)一个正数前面有偶数个“-”号,可以把“-”号一起去掉.
(2)一个正数前面有奇数个“-”号,则化简后只剩一个“-”号.
(3)0前面不论有多少个“+”号或“-”号,化简后仍是0.
【想一想错在哪?】画出数轴,在数轴上表示下列各数的相反数,并把它们的相反数按照数轴上从左到右的顺序排列:1,
-(+2.5),0,-3.
提示:求相反数时对多重符号的化简出现错误,最后导致比较大小也出现错误.
1.2.3 相 反 数
1.掌握相反数的概念,理解它所包含的两种含义.(重点)
2.会求一个数的相反数,理解互为相反数的两个数在数轴上的位置关系.(重点、难点)
3.理解和掌握双重符号的化简规律.(重点)
相反数的定义
1.在数轴上,与原点的距离是6的点有两个,所表示的数分别
为__和___.
2.在数轴上,与原点的距离是10的点有两个,所表示的数分
别为___和____.
6
-6
10
-10
【思考】 1.观察上面两个题中你所填的两组数,各组数有什么
特点?
提示:每组数中的两个数只有符号不同.
2.表示各组数的点在数轴上的位置有什么特点?
提示:与原点的距离相等且分别在原点左右(即关于原点对称).
【总结】 1.相反数的定义:
(1)代数定义:只有_____不同的两个数叫做互为相反数,0的相
反数是__.
(2)几何定义:一般地,设a是一个正数,数轴上与原点的距离
是a的点有___个,它们分别在原点左右,表示-a和a,我们说这
两点关于原点_____,这里-a与a互为相反数.
符号
两
对称
0
2.求一个数的相反数的方法:只改变它的_____,其他部分都
_____.
3.多重符号的化简方法:因为一个数的前面加上“+”号等于
它的_____,一个数的前面加上“-”号等于它的_______,所以
把多重符号化为单一的符号时,如果是正号,可以_________,
如果是负号,取其_______即可.
符号
不变
本身
相反数
省略不写
相反数
(打“√”或“×”)
(1)符号不同的两个数互为相反数.( )
(2)-6的相反数是6.( )
(3)0没有相反数.( )
(4)a的相反数一定是负数.( )
(5)在数轴上离原点4个单位长度的点表示的数是4.( )
(6)在数轴上,表示互为相反数的两个点一定位于原点的两
侧.( )
×
√
×
×
×
×
1 相反数
【例1】分别写出2, , ,-2.5的相反数,并在数轴上标出
各数及它们的相反数,说明各对数在数轴上的位置特点.
【思路点拨】在所求数的前面添上“-”号,即得原数的相反
数→在数轴上表示出各数→观察各对数在数轴上的位置→结论
【自主解答】2的相反数是-2; 的相反数是 ; 的相反数
是 ;-2.5的相反数是2.5.把这些数及它们的相反数表示在数
轴上为:
2和-2, 和 , 和 ,-2.5和2.5,各对数在数轴上分别位
于原点两侧,且到原点的距离相等,即在数轴上表示每对数的
点关于原点对称.
【总结提升】求相反数的方法
1.在原数的前面加“-”号后,再进行符号化简.
2.复杂的数在求相反数前,可先进行符号化简,然后再变号.
2 多重符号的化简
【例2】(1)化简下列各数:
-(+5),-[-(+5)],-{-[-(+5)]}.
(2)猜想:当+5前面有2 013个正号时,化简的结果为______;
当+5前面有2 013个负号时,化简的结果为______;当+5前面
有2 012个负号时,化简的结果为______.
【解题探究】(1)-(+5)表示的意义是+5的_______,所以
-(+5)=___;
-[-(+5)]表示的意义是-(+5)的_______,而
-(+5)=___,所以-[-(+5)]=__;
-{-[-(+5)]}表示的意义是-[-(+5)]的_______,而
-[-(+5)]=__,所以-{-[-(+5)]}=_____.
相反数
-5
相反数
5
相反数
-5
-5
5
(2)①当+5前面只有“+”时,化简的结果的符号怎样?结果是
多少?
②当+5前面有奇数个“-”号时,化简的结果的符号怎样?结
果是多少?
③当+5前面有偶数个“-”号时,化简的结果的符号怎样?结
果是多少?
提示:①为正,5 ②为负,-5 ③为正,5
(3)由探究(2)的结论,能得出例2(2)的猜想吗?
提示:+5 -5 +5
【互动探究】化简数的符号时,结果的符号只与哪种符号有
关?
提示:化简数的符号时,结果的符号与“+”号无关,只与
“-”号的个数有关.当“-”号有偶数个时结果为正;当
“-”号有奇数个时结果为负.
【总结提升】多重符号化简的三个规律
1.把所有的正号去掉.
2.负号的个数是偶数时结果为正数,负号的个数为奇数时结果为负数,简称“奇负偶正”.
3.也可以采用两个同号得正,两个异号得负,分层化简的办法.
注意:多重符号的结果由“-”号的个数决定,与“+”号无关,最后结果的“+”号一般省略不写.
题组一:相反数
1.-7的相反数是( )
A.-7 B.7 C. D.
【解析】选B.与-7只有符号不同的数是7.
2.一个数的相反数是非负数,这个数一定是( )
A.正数或零 B.非零的数
C.负数或零 D.零
【解析】选C.正数的相反数是负数,0的相反数是0,即非负数
的相反数是非正数,即负数或零.
3.如果a=-a,那么表示a的点在数轴上的位置是在( )
A.原点左侧 B.原点右侧
C.原点上或原点右侧 D.原点上
【解析】选D.a=-a表示a与它的相反数-a相等,因为只有0的
相反数等于它本身,故a=0.
4.请你写出一对互为相反数的两个数:________与________.
【解析】只有符号不同的两个数互为相反数,因此写出只有符
号不同的两个数即可.
答案:2 -2(答案不唯一)
数a的相反数
数a的相反数是-a,这里的a是任意有理数,即a可以是正数、负数或0.
(1)当a>0时,-a<0(正数的相反数是负数).
(2)当a<0时,-a>0(负数的相反数是正数).
(3)当a=0时,-a=0(0的相反数是0).
综上可知,a不一定是正数,-a不一定是负数.
5.写出下列各数的相反数:
9,-0.3,-2 .
【解析】9的相反数是-9;-0.3的相反数是0.3;
-2 的相反数是2 .
6.已知m,n互为相反数,求6(m+n)- +2 012的值.
【解析】因为m,n互为相反数,所以m+n=0,所以
6(m+n)- +2 012=0-0+2 012=2 012.
题组二:多重符号的化简
1. 计算-(-5)等于( )
A.5 B.-5
C. D.-
【解析】选A.因为-(-5)表示-5的相反数,
所以-(-5)=5.
2.下列各数:+(-1),-[+(-3)],-(- ),-(-m),+[-(+ )]
其中正数有( )
A.1个 B.2个
C.3个 D.4个
【解析】选B.+(-1)=-1,-[+(-3)]=3,-(- )= ,
+[-(+ )]=- ,-(-m)=m,但m可能是正数,可能是负数,
也可能是0.
3.化简:-(-2 012)=______.
【解析】因为-(-2 012)表示-2 012的相反数,所以
-(-2 012)=2 012.
答案:2 012
4.-(+6)是 的相反数.
【解析】-(+6)=-6,是6的相反数.
答案:6
5.化简下列各数:
(1)-(+7).(2)+(-3).
(3)+(+ ).(4)-[-(- )].
【解析】(1)-(+7)=-7.
(2)+(-3)=-3.
(3)+(+ )= .
(4)-[-(- )]=- .
【归纳整合】多重符号的化简方法
(1)一个正数前面有偶数个“-”号,可以把“-”号一起去掉.
(2)一个正数前面有奇数个“-”号,则化简后只剩一个“-”号.
(3)0前面不论有多少个“+”号或“-”号,化简后仍是0.
【想一想错在哪?】画出数轴,在数轴上表示下列各数的相反数,并把它们的相反数按照数轴上从左到右的顺序排列:1,
-(+2.5),0,-3.
提示:求相反数时对多重符号的化简出现错误,最后导致比较大小也出现错误.
