人教版七年级上册数学课件:1.2.4绝对值 (共16张PPT)
文档属性
| 名称 | 人教版七年级上册数学课件:1.2.4绝对值 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 546.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-29 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
1.2.4 绝 对 值
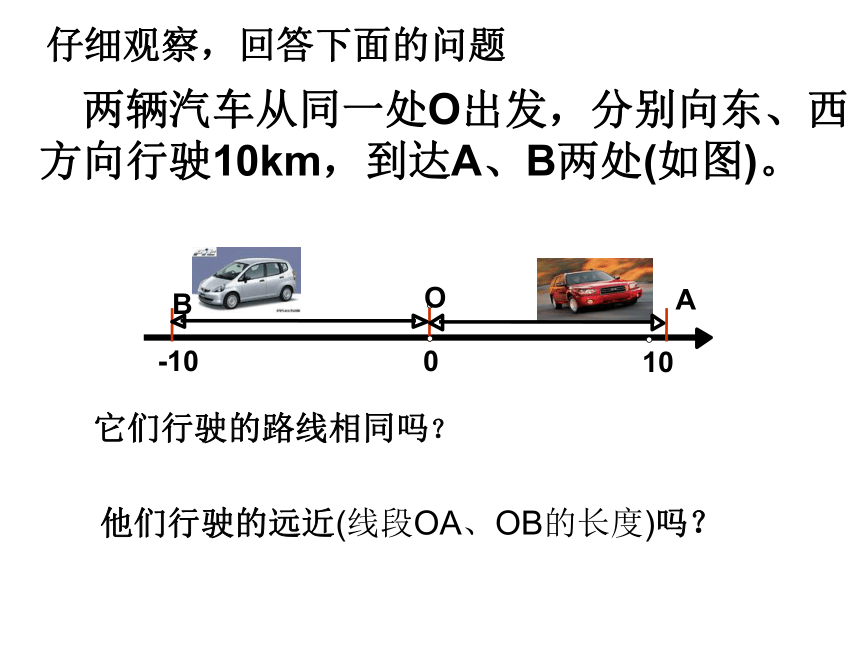
仔细观察,回答下面的问题
它们行驶的路线相同吗?
他们行驶的远近(线段OA、OB的长度)吗?
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图)。
B O A
-10 0 10
由上面问题可以知道,A点到原点的距离是 ,
B点到原点的距离也是
10
10
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作
例如,10和-10它们到原点的距离都是10个单位长度,所以10和-10的绝对值都是10,即
议一议 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0。即 |0|=0
而 原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
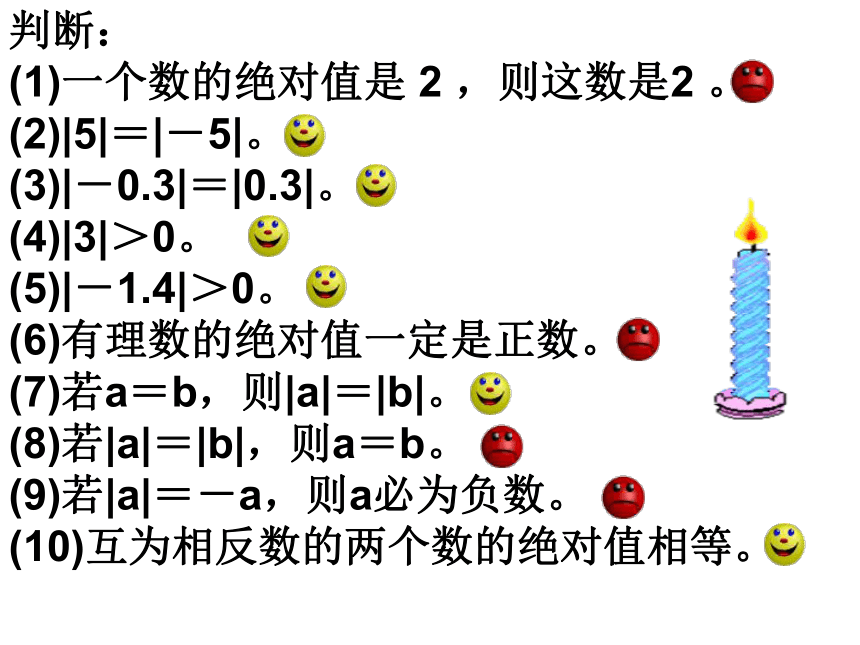
判断:
(1)一个数的绝对值是 2?,则这数是2 。 (2)|5|=|-5|。 (3)|-0.3|=|0.3|。 (4)|3|>0。 (5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。 (8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。 (10)互为相反数的两个数的绝对值相等。
想一想
1) 绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
想一想???
1、三个数a、b、c满足下列条件:a是最小的自然数,b是绝对值最小的数 ,c是相反数等于它本身的数,则a+b+c=?
2如果
则 a=_____,b=_____.
利用绝对值解决实际问题
正式的足球比赛,对足球的质量有严格的规定,下面是6个足球的质量检测结果,用正数记超过规定质量的克数,用负数记不足规定质量的克数,检测结果如下:-25,+30,-10,+20,+15,-40.请指出哪个足球的质量好一些,并用绝对值的知识进行说明.
因为|-10|<|+15|<|+20|<|-25|<|+30|<|-40|.-10的绝对值最小 ,
无论是超过规定质量的克数(正数),还是不足规定质量的克数(负数),它们的绝对值越大说明这个足球的质量与规定质量相差越远,它的质量越差,相反,绝对值越小,说明它的质量与规定质量越接近,它的质量就越好.
所以检测结果为-10克的足球的质量好一些.
判断并改错:
(1)一个数的绝对值等于本身,则这个数一定是正数; ( )
(2)一个数的绝对值等于它的相反数,这个数一定是负数;( )
(3)如果两个数的绝对值相等,那么这两个数一定相等; ( )
(4)如果两个数不相等,那么这两个数的绝对值一定不等;( )
(5)有理数的绝对值一定是非负数; ( )
(6)有理数没有最小的,有理数的绝对值也没有最小的; ( )
(7)两个有理数,绝对值大的反而小; ( )
(8)两个有理数为a 、b,若a >b,则|a|>|b|. ( )
练习:
练习1:____的相反数是它本身,_______的绝对值
是它本身,_______的绝对值是它的相反数.
练习2:|- |的相反数是 ;若| |=2,则 = .
练习3:绝对值小于3.5的整数是 .
练习4:已知: ,则x= ,y= .
-3,-2,-1,0,1,2,3
0
非负数
非正数
±2
-3
2
练习5:有理数a、b在数轴上的位置对应如图1,
试用“>”将a、b、-a、-b、0、2、-2连接起来.
解:
则由图2可知-a >2>b>0>-b>-2>a.
图1
由相反数的意义,
在数轴上画出表示-a、-b的点,如图2所示,
图2
作业:
1.必做题:教科书第15页习题1.2第4、5、6、8题.
2.选做题:(1)教科书第15页习题1.2第10题.
(2)|m|+m ( )
A.可以是负数 B.不可能是负数
C.必是正数 D.可以是正数也可以是负数
温馨提示:
认真完成作业是巩固知识的有效方法!!
B
1、数轴上表示数a的点与原点的距离叫做数a的绝对值。
2、(1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
课堂小结
3、
3、
3、
3、
谢谢大家~
1.2.4 绝 对 值
仔细观察,回答下面的问题
它们行驶的路线相同吗?
他们行驶的远近(线段OA、OB的长度)吗?
两辆汽车从同一处O出发,分别向东、西方向行驶10km,到达A、B两处(如图)。
B O A
-10 0 10
由上面问题可以知道,A点到原点的距离是 ,
B点到原点的距离也是
10
10
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作
例如,10和-10它们到原点的距离都是10个单位长度,所以10和-10的绝对值都是10,即
议一议 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0。即 |0|=0
而 原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
判断:
(1)一个数的绝对值是 2?,则这数是2 。 (2)|5|=|-5|。 (3)|-0.3|=|0.3|。 (4)|3|>0。 (5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。 (8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。 (10)互为相反数的两个数的绝对值相等。
想一想
1) 绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
想一想???
1、三个数a、b、c满足下列条件:a是最小的自然数,b是绝对值最小的数 ,c是相反数等于它本身的数,则a+b+c=?
2如果
则 a=_____,b=_____.
利用绝对值解决实际问题
正式的足球比赛,对足球的质量有严格的规定,下面是6个足球的质量检测结果,用正数记超过规定质量的克数,用负数记不足规定质量的克数,检测结果如下:-25,+30,-10,+20,+15,-40.请指出哪个足球的质量好一些,并用绝对值的知识进行说明.
因为|-10|<|+15|<|+20|<|-25|<|+30|<|-40|.-10的绝对值最小 ,
无论是超过规定质量的克数(正数),还是不足规定质量的克数(负数),它们的绝对值越大说明这个足球的质量与规定质量相差越远,它的质量越差,相反,绝对值越小,说明它的质量与规定质量越接近,它的质量就越好.
所以检测结果为-10克的足球的质量好一些.
判断并改错:
(1)一个数的绝对值等于本身,则这个数一定是正数; ( )
(2)一个数的绝对值等于它的相反数,这个数一定是负数;( )
(3)如果两个数的绝对值相等,那么这两个数一定相等; ( )
(4)如果两个数不相等,那么这两个数的绝对值一定不等;( )
(5)有理数的绝对值一定是非负数; ( )
(6)有理数没有最小的,有理数的绝对值也没有最小的; ( )
(7)两个有理数,绝对值大的反而小; ( )
(8)两个有理数为a 、b,若a >b,则|a|>|b|. ( )
练习:
练习1:____的相反数是它本身,_______的绝对值
是它本身,_______的绝对值是它的相反数.
练习2:|- |的相反数是 ;若| |=2,则 = .
练习3:绝对值小于3.5的整数是 .
练习4:已知: ,则x= ,y= .
-3,-2,-1,0,1,2,3
0
非负数
非正数
±2
-3
2
练习5:有理数a、b在数轴上的位置对应如图1,
试用“>”将a、b、-a、-b、0、2、-2连接起来.
解:
则由图2可知-a >2>b>0>-b>-2>a.
图1
由相反数的意义,
在数轴上画出表示-a、-b的点,如图2所示,
图2
作业:
1.必做题:教科书第15页习题1.2第4、5、6、8题.
2.选做题:(1)教科书第15页习题1.2第10题.
(2)|m|+m ( )
A.可以是负数 B.不可能是负数
C.必是正数 D.可以是正数也可以是负数
温馨提示:
认真完成作业是巩固知识的有效方法!!
B
1、数轴上表示数a的点与原点的距离叫做数a的绝对值。
2、(1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
课堂小结
3、
3、
3、
3、
谢谢大家~
