人教高中数学必修四第一章 三角函数 专题复习(无答案)
文档属性
| 名称 | 人教高中数学必修四第一章 三角函数 专题复习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 526.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 20:30:44 | ||
图片预览




文档简介
三角函数专题复习
三角函数的定义
第一定义:角的终边与单位圆的交点为则角的三角函数为:
第二定义:角的终边上任意一点为则角的三角函数为:
1. 已知角的终边上一点为则求角的三个三角函数。
2.已知角终边上一点,且sin,求
1、 同角的三角函数关系
平方关系: 商数关系: .
1.若是第二象限的角,且,则( )
A. B. C. D.
2、已知,且是第四象限的角,则 ( )
A . B. C. D.
3.已知,,则 。
4. 已知=2,求
(I)的值; (II)的值.
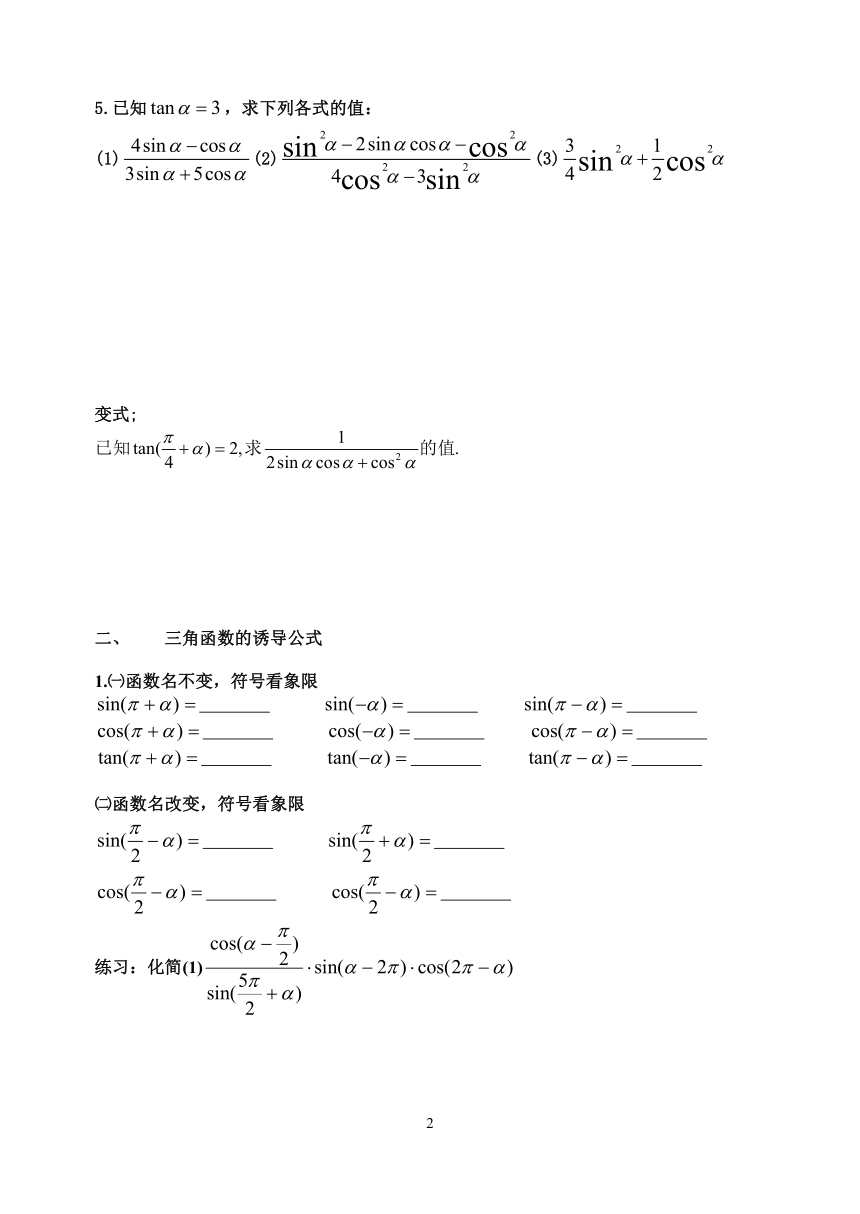
5.已知,求下列各式的值:
(1)(2)(3)
变式;
2、 三角函数的诱导公式
1.㈠函数名不变,符号看象限
㈡函数名改变,符号看象限
练习:化简(1)
(2).
(3)已知,求
3、 三角恒等变换
= =
1. (1)已知为第三象限角;
求 ,
(2)已知函数.
(I)若是第一象限角,且.求的值;
(II)求使成立的x的取值集合.
2.化简:
eq \f(,cos10°-)的值为
若,化简
3(1)已知设,,则的值是________
(2)已知,则的值等于( )
A. - B. C. D. -
(3) 已知等于( )
A.3 B.6 C.12 D.
(4)已知
4(1)已知.
(I)求sinx-cosx的值; (Ⅱ)求的值.
(2)已知,,<< ,求的值。
5(1):化简
(2) 的值为____ _.
(3)在△ABC中,若sinBsinC=cos2,则△ABC是( )
A.等边三角形 B.等腰三角形
C.不等边三角形 D.直角三角形
6.(1)若且求
(2)已知求的值。
(3) 知求的值
7(1). 已知则____ _.
(2)若则的值为( )
A. B. C. D.
4、 三角函数图象与性质
函数 y=sinx y=cosx y=tanx
图 象
定义域
值域
单调性
最值
奇偶性
对称性 对称中心
对称轴
周期性
(一)五点法作图;作出在上的图像。
(二)如何y=sinx的图象变换得到y=3sin(2x+)的图象
1.将函数的图像上所有的点向右平行移动个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图像的函数解析式是
(A) (B)
(C) (D)
2.将的图像向左平移(个单位长度后,得到的图像,则=( )
3.为得到函数y=sin(2x-)的图象可以将函数y=cos2x的图象向( )平移( )个单位长度 A.右, B.右, C.左, D.左,
4.已知函数(A>0,>0,0<)的两个邻近的最值点为()和(),则这个函数的解析式为____________________.
5已知函数=Acos()的图象如图所示,,则=( )
A. B. C.- D.
6.已知函数f(x)=Asin(ωx+φ) (A>0,ω>0,|φ|<,x∈R)的图象的一部分如图所示.求函数f(x)的解析式.
7.已知函数(A>O, >0,<)的最小正周期是,最小值是-2,且图象经过点M(),求这个函数的解析式.
8. 函数()的最大值为3, 其图像相邻两条对称轴之间的距离为,求函数的解析式;
(三)性质的研究
1、函数的值域是
A. B. C. D.
2.已知函数.
(I)求的最小正周期;(II)求的的最大值和最小值;
(III)若,求的值.
3.已知函数。
(Ⅰ)求的最小正周期,对称轴方程,对称中心:
(Ⅱ)求在区间上的最大值和最小值。
3.函数y=sin2xcos2x的最小正周期是 ( )
(A)2π (B)4π (C) (D)
4.已知函数,,则的最小正周期是
5.已知函数
(1)求的最小正周期和最小值;
(2)已知,求证:
6. (1)若函数为偶函数,则的一个值可以是( )
(2)若函数为奇函数,则的一个值可以是( )
A. B. C. D.
.
7(1).如果函数的图像关于点中心对称,那么的最小值为( )
(2)如果函数的图像关于对称,那么的最小值为( )
(A) (B) (C) (D)
(3).若函数f(x)= 对任意x都有f()=f()
(1)求f()(2)求的最小正值
(3)当取最小正值时若求f(x)的最大值与最小值
8已知函数,.求:
(I) 函数的最大值及取得最大值的自变量的集合;
(II) 函数的单调增区间.
9.已知函数f(x)=sin .
(1)求时的单调递增区间;(2)求时的函数的最值,及对应的x的取 (3)画出函数y=f(x)在区间[0,π]上的图象.
10. 已知函数
(1)求的周期和单调增区间
(2)若关于x的方程,求实数m的取值范围。
PAGE
1
