沪科版九年级下数学第24章圆单元测试卷及答案
文档属性
| 名称 | 沪科版九年级下数学第24章圆单元测试卷及答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 390.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 00:00:00 | ||
图片预览



文档简介
沪科版九年级数学下册 第24章 圆 测试卷及答案
沪科版九年级数学下册 第24章 圆 测试卷
(时间:120分钟 满分:150分)
姓名: 班级: 得分:
一、选择题(本大题共10小题,每小题4分,满分40分)
1.观察下列图形,其中既是轴对称图形又是中心对称图形
2.下列命题中,正确的有( )
①顶点在圆周上的角是圆周角; ②圆周角的度数等于圆心角度数的一半;
③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;
⑤同弧所对的圆周角相等
A.①②③ B.③④⑤ C.①②⑤ D.②④⑤
3.如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
4.已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是( )
A.4x B.8x C.12x D.16x
5.如图,正六边形ABCDEF内接于OO,正六边形的周长是12,则OO的半径是
A. B.2 C. D.
6.如图,AB是OO的弦,半径OC⊥AB于点D,下列判断中错误的是( )
A.OD=DC B. AC=BC C.AD=BD D.∠AOC=∠AOB
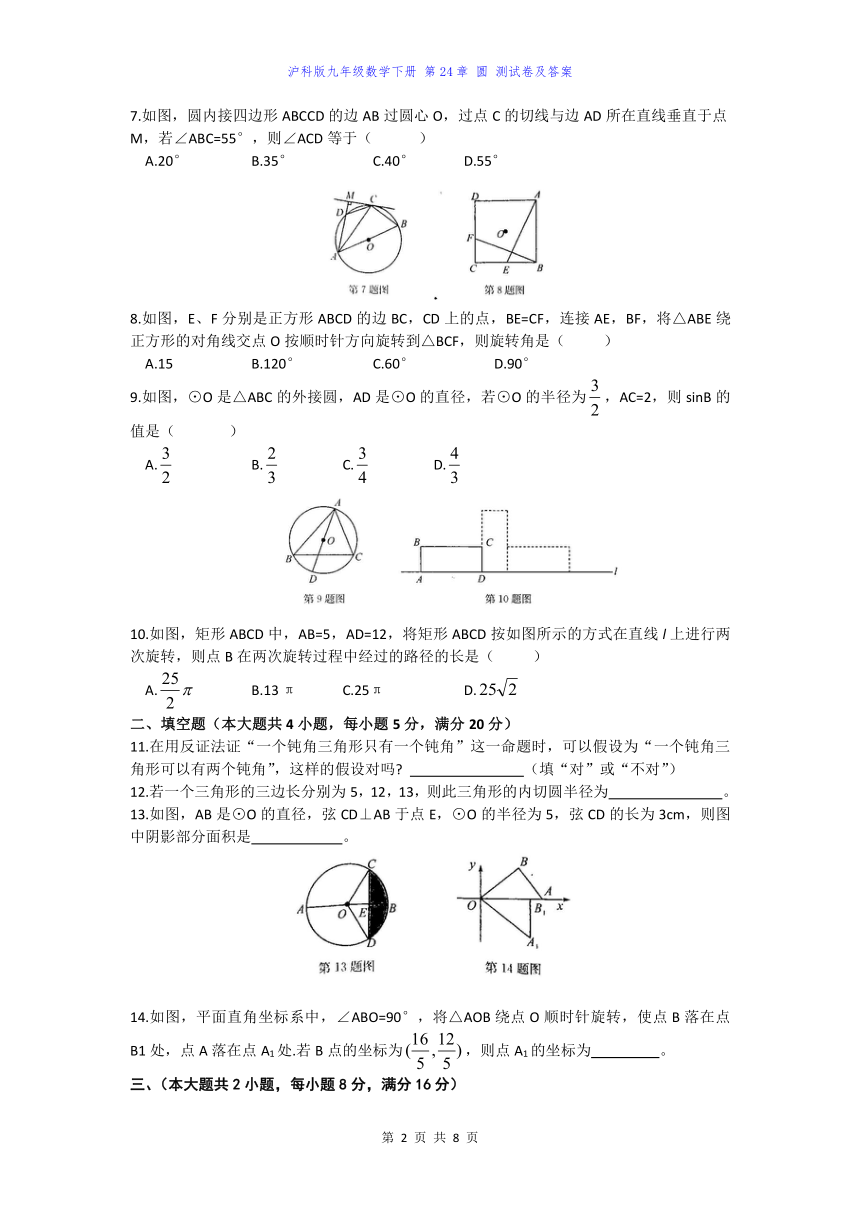
7.如图,圆内接四边形ABCCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
8.如图,E、F分别是正方形ABCD的边BC,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF,则旋转角是( )
A.15 B.120° C.60° D.90°
9.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为,AC=2,则sinB的值是( )
A. B. C. D.
10.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
A. B.13 π C.25π D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在用反证法证“一个钝角三角形只有一个钝角”这一命题时,可以假设为“一个钝角三角形可以有两个钝角”,这样的假设对吗? (填“对”或“不对”)
12.若一个三角形的三边长分别为5,12,13,则此三角形的内切圆半径为 。
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为5,弦CD的长为3cm,则图中阴影部分面积是 。
14.如图,平面直角坐标系中,∠ABO=90°,将△AOB绕点O顺时针旋转,使点B落在点B1处,点A落在点A1处.若B点的坐标为,则点A1的坐标为 。
三、(本大题共2小题,每小题8分,满分16分)
15.如图,等腰△OAB中,OA=OB,以点O为圆心作圆与底边AB相切于点C.
求证:AC=BC.
16.如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
四、(本大题共2小题,每小题8分,满分16分)
17.如图所示,AB是⊙O的直径,点为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD、AD.若∠ACD=30°.求∠DBA的度数.
18.如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的⊙P圆心在射线OA上,开始时,PO=6cm.如果OP以1cm/s的速度由A向B的方向移动,那么当OP运动时间t(s)满足什么条件时,OP与直线(CLD相交.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2).请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标,
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)面出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.
20.如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形.
(1)求这个扇形的面积(结果保留π);
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.
六、(本题满分12分)
21.如图是“明清影视城”的圆弧形门,黄红同学到影视城游玩,很想知道这扇门的相关数据.于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少?
七、(本题满分12分)
22.如图所示,圆O是△ABC的外接圆,∠BAC与∠ABC、的平分线相交于点I,延长AI交圆O于点D,连接BD,DC.
(1)求证:BD=D=DI;
(2)若圆O的半径为10cm,∠BAC=120°,求△BDC的面积,
八、(本题满分14分)
23.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求的值;
(3)若EA=EF=1,求圆O的半径.
第24章测试卷答案
1.D 2.B 3.A 4.C 5.B 6.A 7.A 8.D 9.B 10.A
11.不对
12.2
13.
14.(4,一3)
15.证明:∵AB切⊙O于点C,∴OC⊥AB
∵OA=OB,∴AC=BC.
16.(1)旋转角的度数为60°.
(2)证明:由题意可知:△ABC≌△A1BC1,
∴A1B=AB.∠C=∠C,由(1)知:∠ABA1=60°,∴△ABA为等边三角形,
∴∠BAA1=60°.而∠CBC1=60°,
∴∠BAA1=∠CBC1,
∴AA1∥BC,
∴∠A1AC=∠C.又∵∠C=∠C1,
∴∠A1AC=∠C1.
17.解:连接OD,∵CA,CD是⊙O的切线,
∴OA⊥AC,OD⊥CD.
∴∠OAC=∠ODC=90°,
∵∠ACD=30°∴∠AOD=360°-∠C-∠OAC一∠ODC=150°,
∴∠BOD=30°
∵OB=OD,
∴∠DBA=∠ODB=(180°-30°)=75°.
18.解:(1)如图,当OP运动到⊙P1与CD相切时.可得P1E=1.又因为∠AOC=30°,
所以OP1=2P1E=2×1=2(cm),
所以⊙P运动到OP1用的时间为.
(2)当⊙P继续向B移动到心P2的位置时.同理可得t2=8(s).
综上所述.当419.(1)△A1B1C1如图所示,此时A1的坐标为(一2,2);
(2)△A2B2C2如图所示,此时A2的坐标为(4,0);
(3)△A3B3C3如图所示、此时A3的坐标为(一4,0).
20.解:(1)连接BC.由勾股定理求得:AB=AC=,
(2)连接AO并延长,与弧BC和⊙O交于E,F,EF=AF-AE=2-2,
弧BC的长:
∵2r=
∴圆锥的底面直径为2r=
∵.
∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
21.解:如图,连接AC.作AC的中垂线交AC于G.交BD于N.交圆的另一点为M.由垂径定
理可知,MN为圆的直径,N点即为圆弧形所在的圆与地面的切点.取MN的中点O,则
O为圆心.连接 OA,OC,又AB⊥BD,CD⊥BD,
∴AB∥CD,又∵AB=CD
∴四边形ABDC为矩形,
∴AC=BD=200cm,GN=AB=CD=20cm.
∴AG=GC=AC=100cm
设⊙O的半径为R.由勾股定理,得OA2=OG2+AG2,即R2=(R一20)2+1002.
解得R=260cm,∴MN=2R=520cm.
答:这个圆弧形门的最高点离地面的高度是520cm.
22.(1)证明:∵AI平分∠BAC,∴∠BAD=∠DAC,∴BD=DC.
∵BI平分∠ABC,∴∠ABI=∠CBI,
∵∠BAD=∠DAC,∠DBC=∠DAC,
∴∠BAD=∠DBC,又∠DBI=∠DBC+∠CBI,∠DIB=∠ABI+∠BAD
∴∠DBI=∠DIB
∴△BDI为等腰三角形,∴BD=ID,.BD=DC=DI.
(2)解:当∠BAC=120°时,△ABC为钝角三角形,∴圆心O在△ABC外,连接OB,OD,
OC,
∴∠DOC=∠BOD=2,∠BAD =120°,
∴∠DBC=∠DCB=60°,
∴△BDC为正三角形.又知OB=10cm,
∴BD=2OBsin60"=2×10×= cm,
∴S△BDC= cm.
23.(1)证明:连接OD,如图1.
∵OB=OD∴△ODB是等腰二角形,
∴∠OBD=∠ODB①,
在△ABC中,∵AB=AC.∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB
∴OD∥AC
∵DH⊥AC
∴DH⊥OD
∴DH是圆O的切线;
(2)解:如图2,在⊙O中.∵∠E=∠B,
∴.由(1)可知∠E=∠B=∠C,
∴△EDC是等腰三角形,
∵DH⊥AC,且点A是EH中点,设AE=x,E=4x,则AC=3x,连接AD,则在⊙O中,∠ADB=90°,AD⊥BD,
∵AB=AC,∴D是BC的中点,∴OD是△ABC的中位线,
∴OD//AC.OD=AC=
∵OD//AC.∴∠E=∠ODF,在△AEF和△ODF中,
∠E=∠ODF,∠OFD=∠AFE,
∴△AEF∽△ODF,
∴,
∴
(3)解:如图2.设⊙O的半径为r,即OD=OB=r,
∵EF=EA,∴∠EFA=∠EAF,
∵OD/∥EC.
∴∠FOD=∠EAF,则∠FOD=∠EAF=∠EFA=∠OFD.
∴DF=OD=r,∴DE=DF+EF=r+1.
∴BD=CD=DE=r+1,
在⊙O中,∠BDE=∠EAB.∴∠BFD=∠EFA=∠EAB=∠BDE,
∴BF=BD,△BDF是等腰三角形.
∴BF=BD=r+1.
∴AF=AB-BF=2OB-BF=2r-(1+r)=r-1.
在ABFD 和△EFA中,
∠BFD=∠EFA
∠B=∠E.
∴△BFD∽EFA,
∴,则
解得:,(舍).
综上所述、⊙O的半径为
沪科版九年级数学下册 第24章 圆 测试卷
(时间:120分钟 满分:150分)
姓名: 班级: 得分:
一、选择题(本大题共10小题,每小题4分,满分40分)
1.观察下列图形,其中既是轴对称图形又是中心对称图形
2.下列命题中,正确的有( )
①顶点在圆周上的角是圆周角; ②圆周角的度数等于圆心角度数的一半;
③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;
⑤同弧所对的圆周角相等
A.①②③ B.③④⑤ C.①②⑤ D.②④⑤
3.如图,将正方形ABCD中的阴影三角形绕点A顺时针旋转90°后,得到的图形为( )
4.已知圆锥的母线长为6,将其侧面沿着一条母线展开后所得扇形的圆心角为120°,则该扇形的面积是( )
A.4x B.8x C.12x D.16x
5.如图,正六边形ABCDEF内接于OO,正六边形的周长是12,则OO的半径是
A. B.2 C. D.
6.如图,AB是OO的弦,半径OC⊥AB于点D,下列判断中错误的是( )
A.OD=DC B. AC=BC C.AD=BD D.∠AOC=∠AOB
7.如图,圆内接四边形ABCCD的边AB过圆心O,过点C的切线与边AD所在直线垂直于点M,若∠ABC=55°,则∠ACD等于( )
A.20° B.35° C.40° D.55°
8.如图,E、F分别是正方形ABCD的边BC,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线交点O按顺时针方向旋转到△BCF,则旋转角是( )
A.15 B.120° C.60° D.90°
9.如图,⊙O是△ABC的外接圆,AD是⊙O的直径,若⊙O的半径为,AC=2,则sinB的值是( )
A. B. C. D.
10.如图,矩形ABCD中,AB=5,AD=12,将矩形ABCD按如图所示的方式在直线l上进行两次旋转,则点B在两次旋转过程中经过的路径的长是( )
A. B.13 π C.25π D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在用反证法证“一个钝角三角形只有一个钝角”这一命题时,可以假设为“一个钝角三角形可以有两个钝角”,这样的假设对吗? (填“对”或“不对”)
12.若一个三角形的三边长分别为5,12,13,则此三角形的内切圆半径为 。
13.如图,AB是⊙O的直径,弦CD⊥AB于点E,⊙O的半径为5,弦CD的长为3cm,则图中阴影部分面积是 。
14.如图,平面直角坐标系中,∠ABO=90°,将△AOB绕点O顺时针旋转,使点B落在点B1处,点A落在点A1处.若B点的坐标为,则点A1的坐标为 。
三、(本大题共2小题,每小题8分,满分16分)
15.如图,等腰△OAB中,OA=OB,以点O为圆心作圆与底边AB相切于点C.
求证:AC=BC.
16.如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连接AA1.
(1)写出旋转角的度数;
(2)求证:∠A1AC=∠C1.
四、(本大题共2小题,每小题8分,满分16分)
17.如图所示,AB是⊙O的直径,点为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD、AD.若∠ACD=30°.求∠DBA的度数.
18.如图,直线AB,CD相交于点O,∠AOC=30°,半径为1cm的⊙P圆心在射线OA上,开始时,PO=6cm.如果OP以1cm/s的速度由A向B的方向移动,那么当OP运动时间t(s)满足什么条件时,OP与直线(CLD相交.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,2).请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出A1的坐标,
(2)画出△ABC绕点B逆时针旋转90°后得到的△A2B2C2,并写出A2的坐标.
(3)面出△A2B2C2关于原点O成中心对称的△A3B3C3,并写出A3的坐标.
20.如图,从一个直径是2的圆形铁皮中剪下一个圆心角为90°的扇形.
(1)求这个扇形的面积(结果保留π);
(2)在剩下的三块余料中,能否从第③块余料中剪出一个圆作为底面与此扇形围成一个圆锥?请说明理由.
六、(本题满分12分)
21.如图是“明清影视城”的圆弧形门,黄红同学到影视城游玩,很想知道这扇门的相关数据.于是她从景点管理人员处打听到:这个圆弧形门所在的圆与水平地面是相切的,AB=CD=20cm,BD=200cm,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮助黄红同学计算出这个圆弧形门的最高点离地面的高度是多少?
七、(本题满分12分)
22.如图所示,圆O是△ABC的外接圆,∠BAC与∠ABC、的平分线相交于点I,延长AI交圆O于点D,连接BD,DC.
(1)求证:BD=D=DI;
(2)若圆O的半径为10cm,∠BAC=120°,求△BDC的面积,
八、(本题满分14分)
23.如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求的值;
(3)若EA=EF=1,求圆O的半径.
第24章测试卷答案
1.D 2.B 3.A 4.C 5.B 6.A 7.A 8.D 9.B 10.A
11.不对
12.2
13.
14.(4,一3)
15.证明:∵AB切⊙O于点C,∴OC⊥AB
∵OA=OB,∴AC=BC.
16.(1)旋转角的度数为60°.
(2)证明:由题意可知:△ABC≌△A1BC1,
∴A1B=AB.∠C=∠C,由(1)知:∠ABA1=60°,∴△ABA为等边三角形,
∴∠BAA1=60°.而∠CBC1=60°,
∴∠BAA1=∠CBC1,
∴AA1∥BC,
∴∠A1AC=∠C.又∵∠C=∠C1,
∴∠A1AC=∠C1.
17.解:连接OD,∵CA,CD是⊙O的切线,
∴OA⊥AC,OD⊥CD.
∴∠OAC=∠ODC=90°,
∵∠ACD=30°∴∠AOD=360°-∠C-∠OAC一∠ODC=150°,
∴∠BOD=30°
∵OB=OD,
∴∠DBA=∠ODB=(180°-30°)=75°.
18.解:(1)如图,当OP运动到⊙P1与CD相切时.可得P1E=1.又因为∠AOC=30°,
所以OP1=2P1E=2×1=2(cm),
所以⊙P运动到OP1用的时间为.
(2)当⊙P继续向B移动到心P2的位置时.同理可得t2=8(s).
综上所述.当4
(2)△A2B2C2如图所示,此时A2的坐标为(4,0);
(3)△A3B3C3如图所示、此时A3的坐标为(一4,0).
20.解:(1)连接BC.由勾股定理求得:AB=AC=,
(2)连接AO并延长,与弧BC和⊙O交于E,F,EF=AF-AE=2-2,
弧BC的长:
∵2r=
∴圆锥的底面直径为2r=
∵.
∴不能在余料③中剪出一个圆作为底面与此扇形围成圆锥.
21.解:如图,连接AC.作AC的中垂线交AC于G.交BD于N.交圆的另一点为M.由垂径定
理可知,MN为圆的直径,N点即为圆弧形所在的圆与地面的切点.取MN的中点O,则
O为圆心.连接 OA,OC,又AB⊥BD,CD⊥BD,
∴AB∥CD,又∵AB=CD
∴四边形ABDC为矩形,
∴AC=BD=200cm,GN=AB=CD=20cm.
∴AG=GC=AC=100cm
设⊙O的半径为R.由勾股定理,得OA2=OG2+AG2,即R2=(R一20)2+1002.
解得R=260cm,∴MN=2R=520cm.
答:这个圆弧形门的最高点离地面的高度是520cm.
22.(1)证明:∵AI平分∠BAC,∴∠BAD=∠DAC,∴BD=DC.
∵BI平分∠ABC,∴∠ABI=∠CBI,
∵∠BAD=∠DAC,∠DBC=∠DAC,
∴∠BAD=∠DBC,又∠DBI=∠DBC+∠CBI,∠DIB=∠ABI+∠BAD
∴∠DBI=∠DIB
∴△BDI为等腰三角形,∴BD=ID,.BD=DC=DI.
(2)解:当∠BAC=120°时,△ABC为钝角三角形,∴圆心O在△ABC外,连接OB,OD,
OC,
∴∠DOC=∠BOD=2,∠BAD =120°,
∴∠DBC=∠DCB=60°,
∴△BDC为正三角形.又知OB=10cm,
∴BD=2OBsin60"=2×10×= cm,
∴S△BDC= cm.
23.(1)证明:连接OD,如图1.
∵OB=OD∴△ODB是等腰二角形,
∴∠OBD=∠ODB①,
在△ABC中,∵AB=AC.∴∠ABC=∠ACB②,
由①②得:∠ODB=∠OBD=∠ACB
∴OD∥AC
∵DH⊥AC
∴DH⊥OD
∴DH是圆O的切线;
(2)解:如图2,在⊙O中.∵∠E=∠B,
∴.由(1)可知∠E=∠B=∠C,
∴△EDC是等腰三角形,
∵DH⊥AC,且点A是EH中点,设AE=x,E=4x,则AC=3x,连接AD,则在⊙O中,∠ADB=90°,AD⊥BD,
∵AB=AC,∴D是BC的中点,∴OD是△ABC的中位线,
∴OD//AC.OD=AC=
∵OD//AC.∴∠E=∠ODF,在△AEF和△ODF中,
∠E=∠ODF,∠OFD=∠AFE,
∴△AEF∽△ODF,
∴,
∴
(3)解:如图2.设⊙O的半径为r,即OD=OB=r,
∵EF=EA,∴∠EFA=∠EAF,
∵OD/∥EC.
∴∠FOD=∠EAF,则∠FOD=∠EAF=∠EFA=∠OFD.
∴DF=OD=r,∴DE=DF+EF=r+1.
∴BD=CD=DE=r+1,
在⊙O中,∠BDE=∠EAB.∴∠BFD=∠EFA=∠EAB=∠BDE,
∴BF=BD,△BDF是等腰三角形.
∴BF=BD=r+1.
∴AF=AB-BF=2OB-BF=2r-(1+r)=r-1.
在ABFD 和△EFA中,
∠BFD=∠EFA
∠B=∠E.
∴△BFD∽EFA,
∴,则
解得:,(舍).
综上所述、⊙O的半径为
