高中物理人教版选修3-4 第十三章 光 高考真题集训 Word版含解析
文档属性
| 名称 | 高中物理人教版选修3-4 第十三章 光 高考真题集训 Word版含解析 |
|
|
| 格式 | zip | ||
| 文件大小 | 364.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-26 08:56:51 | ||
图片预览



文档简介
第十三章 高考真题集训
一、选择题
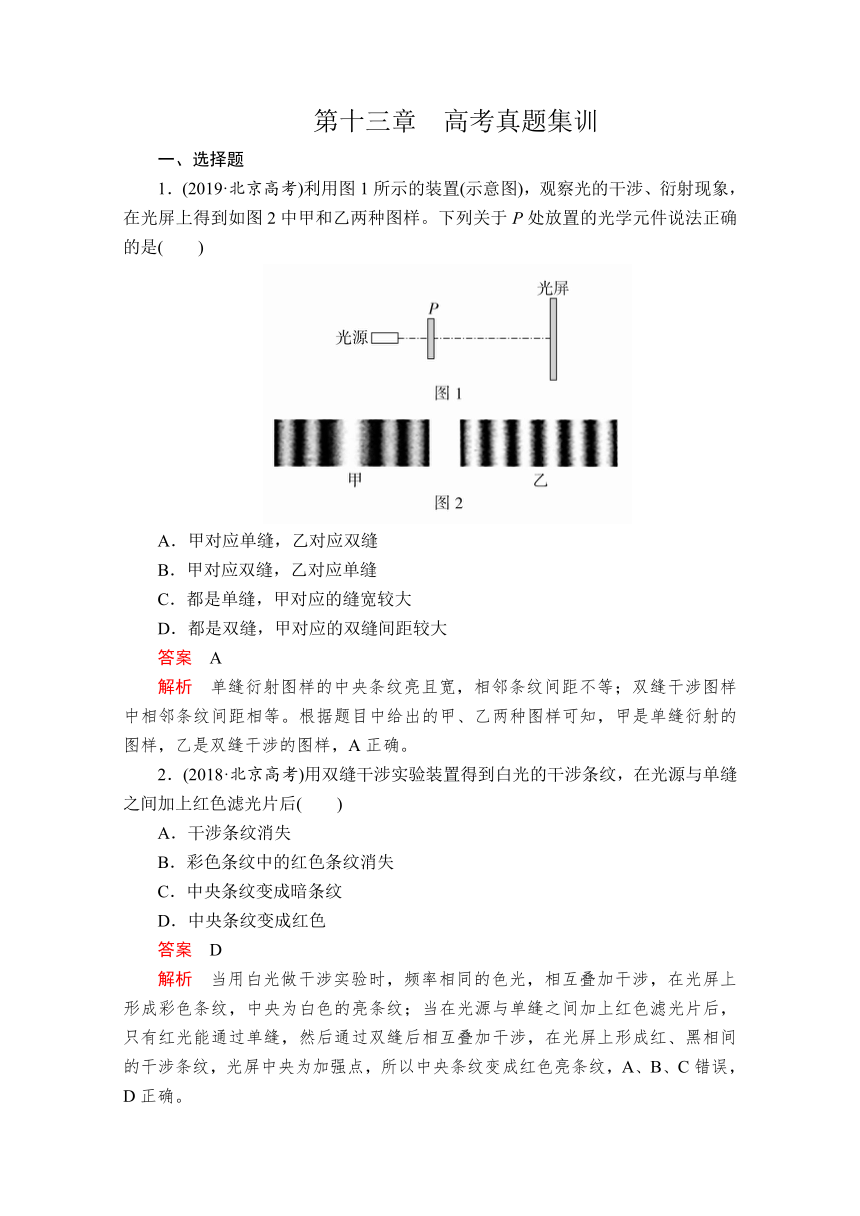
1.(2019·北京高考)利用图1所示的装置(示意图),观察光的干涉、衍射现象,在光屏上得到如图2中甲和乙两种图样。下列关于P处放置的光学元件说法正确的是( )
A.甲对应单缝,乙对应双缝
B.甲对应双缝,乙对应单缝
C.都是单缝,甲对应的缝宽较大
D.都是双缝,甲对应的双缝间距较大
答案 A
解析 单缝衍射图样的中央条纹亮且宽,相邻条纹间距不等;双缝干涉图样中相邻条纹间距相等。根据题目中给出的甲、乙两种图样可知,甲是单缝衍射的图样,乙是双缝干涉的图样,A正确。
2.(2018·北京高考)用双缝干涉实验装置得到白光的干涉条纹,在光源与单缝之间加上红色滤光片后( )
A.干涉条纹消失
B.彩色条纹中的红色条纹消失
C.中央条纹变成暗条纹
D.中央条纹变成红色
答案 D
解析 当用白光做干涉实验时,频率相同的色光,相互叠加干涉,在光屏上形成彩色条纹,中央为白色的亮条纹;当在光源与单缝之间加上红色滤光片后,只有红光能通过单缝,然后通过双缝后相互叠加干涉,在光屏上形成红、黑相间的干涉条纹,光屏中央为加强点,所以中央条纹变成红色亮条纹,A、B、C错误,D正确。
3.(2017·全国卷Ⅱ)(多选)在双缝干涉实验中,用绿色激光照射在双缝上,在缝后的屏幕上显示出干涉图样。若要增大干涉图样中两相邻亮条纹的间距,可选用的方法是( )
A.改用红色激光
B.改用蓝色激光
C.减小双缝间距
D.将屏幕向远离双缝的位置移动
E.将光源向远离双缝的位置移动
答案 ACD
解析 在双缝干涉实验中两相邻亮条纹的间距Δx=λ,因此要增大干涉图样中两相邻亮条纹的间距可减小双缝间的距离,增大屏幕与双缝的距离,换用波长更长或频率更小的光做光源,故选A、C、D。
4.(2017·北京高考) 如图所示,一束可见光穿过平行玻璃砖后,变为a、b两束单色光。如果光束b是蓝光,则光束a可能是( )
A.红光 B.黄光
C.绿光 D.紫光
答案 D
解析 解法一:光的偏折程度越大,则折射率越大,光的频率越大。题中a光的偏折程度大于b光的偏折程度,则玻璃对a光的折射率大于对b光的折射率,a光的频率大于b光的频率,只有D正确。
解法二:本题是单项选择,题中A、B、C光的频率均比蓝光的小,只有D光的频率比蓝光的大,可以直接判定D正确。
二、填空题
5.(2018·全国卷Ⅰ) 如图,△ABC为一玻璃三棱镜的横截面,∠A=30°。一束红光垂直AB边射入,从AC边上的D点射出,其折射角为60°,则玻璃对红光的折射率为________。若改用蓝光沿同一路径入射,则光线在D点射出时的折射角________(填“小于”“等于”或“大于”)60°。
答案 大于
解析 由光路可逆性,根据题述和图示可知,i=60°,r=30°,由折射定律,玻璃对红光的折射率n==。若改用蓝光沿同一路径入射,由于玻璃对蓝光的折射率大于玻璃对红光的折射率,则光线在D点射出时的折射角大于60°。
6.(2019·江苏高考)将两支铅笔并排放在一起,中间留一条狭缝,通过这条狭缝去看与其平行的日光灯,能观察到彩色条纹,这是由于光的________(选填“折射”“干涉”或“衍射”)。当缝的宽度________(选填“远大于”或“接近”)光波的波长时,这种现象十分明显。
答案 衍射 接近
解析 将两支铅笔并排放在一起,中间留一条狭缝,通过这条狭缝去看与其平行的日光灯,能观察到彩色条纹,这是由于光的衍射产生的;当缝的宽度与光波的波长接近或比光波的波长更小时,衍射现象很明显。
7.(2018·江苏高考)两束单色光A、B的波长分别为λA、λB,且λA>λB,则________(选填“A”或“B”)在水中发生全反射时的临界角较大。用同一装置进行杨氏双缝干涉实验时,可以观察到________(选填“A”或“B”)产生的条纹间距较大。
答案 A A
解析 波长越长,频率越小,折射率越小,根据临界角的正弦sinC=,可知波长越长临界角越大,所以A光在水中发生全反射时的临界角较大;双缝干涉条纹的间距Δx=λ,因为A光的波长较长,所以A光产生的条纹间距较大。
三、实验题
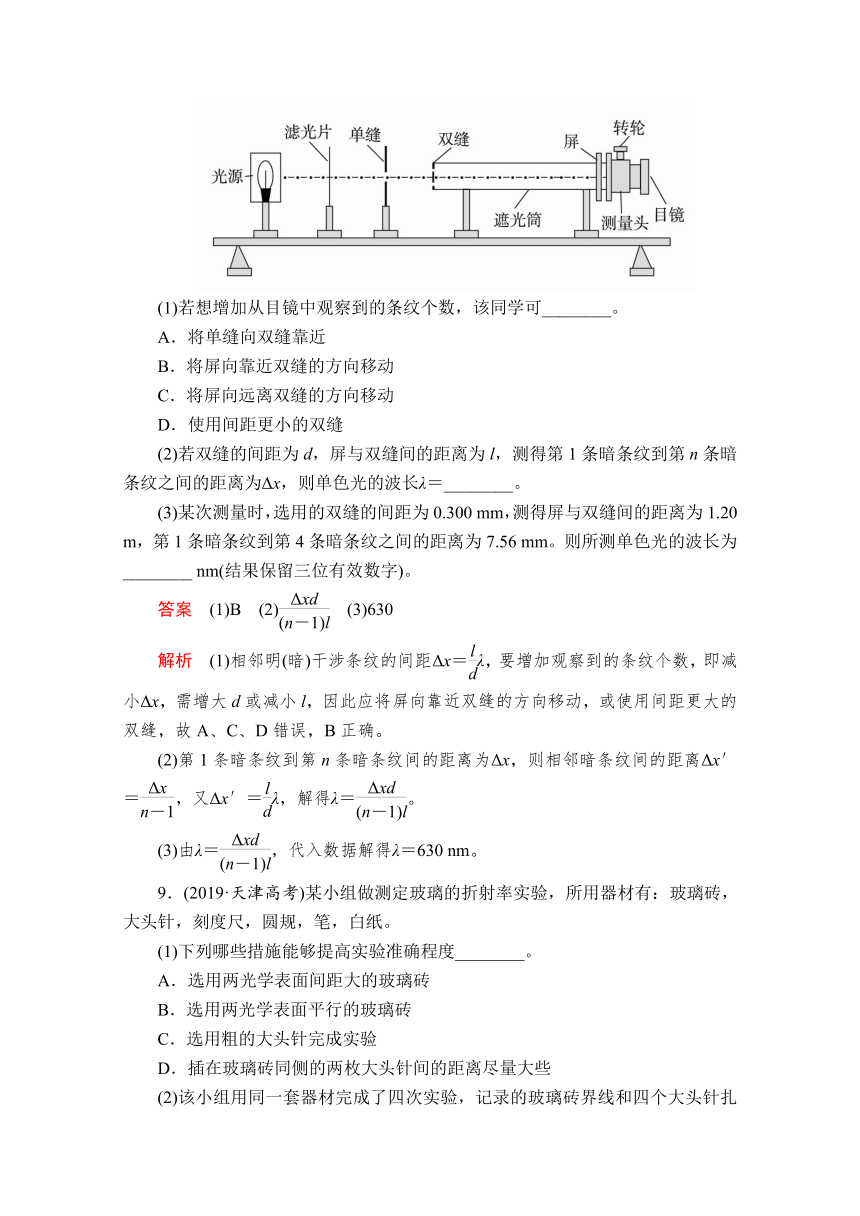
8.(2019·全国卷Ⅱ)某同学利用图示装置测量某种单色光的波长。实验时,接通电源使光源正常发光;调整光路,使得从目镜中可以观察到干涉条纹。回答下列问题:
(1)若想增加从目镜中观察到的条纹个数,该同学可________。
A.将单缝向双缝靠近
B.将屏向靠近双缝的方向移动
C.将屏向远离双缝的方向移动
D.使用间距更小的双缝
(2)若双缝的间距为d,屏与双缝间的距离为l,测得第1条暗条纹到第n条暗条纹之间的距离为Δx,则单色光的波长λ=________。
(3)某次测量时,选用的双缝的间距为0.300 mm,测得屏与双缝间的距离为1.20 m,第1条暗条纹到第4条暗条纹之间的距离为7.56 mm。则所测单色光的波长为________ nm(结果保留三位有效数字)。
答案 (1)B (2) (3)630
解析 (1)相邻明(暗)干涉条纹的间距Δx=λ,要增加观察到的条纹个数,即减小Δx,需增大d或减小l,因此应将屏向靠近双缝的方向移动,或使用间距更大的双缝,故A、C、D错误,B正确。
(2)第1条暗条纹到第n条暗条纹间的距离为Δx,则相邻暗条纹间的距离Δx′=,又Δx′=λ,解得λ=。
(3)由λ=,代入数据解得λ=630 nm。
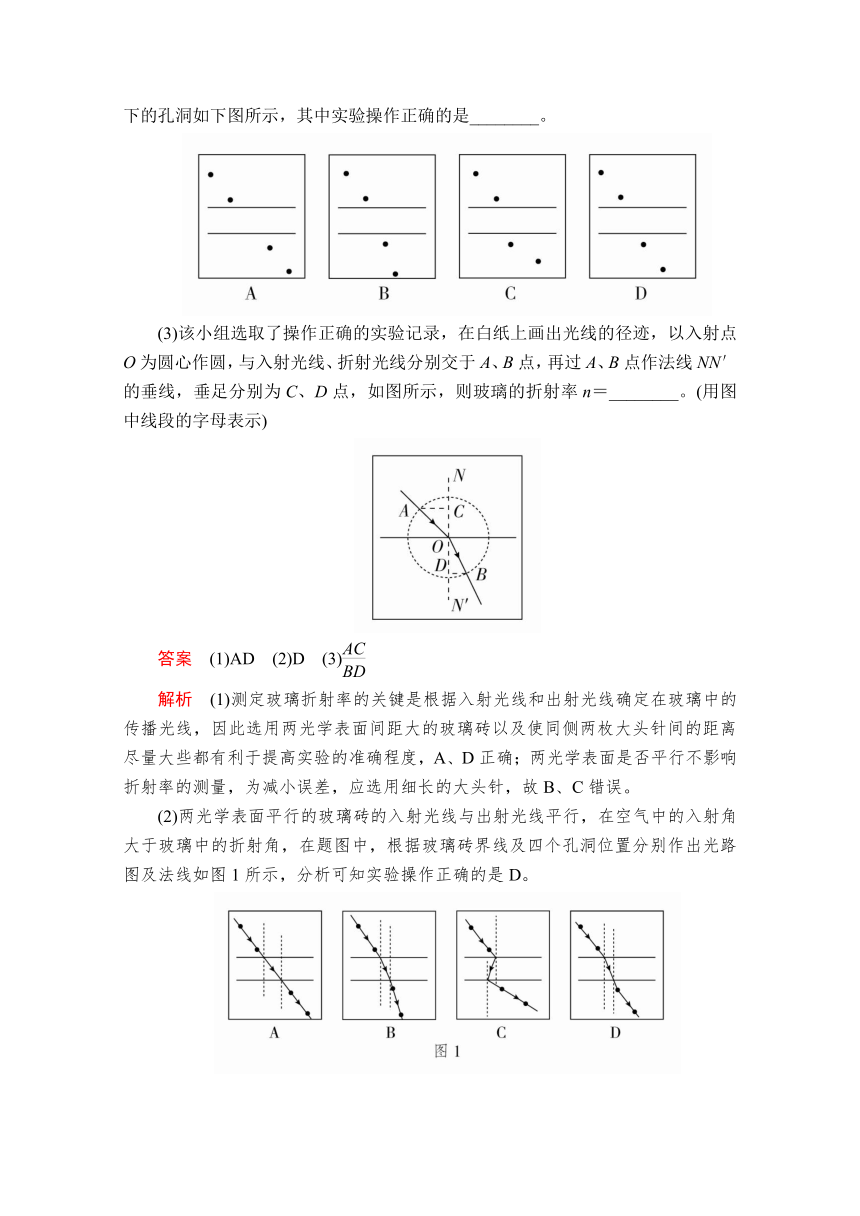
9.(2019·天津高考)某小组做测定玻璃的折射率实验,所用器材有:玻璃砖,大头针,刻度尺,圆规,笔,白纸。
(1)下列哪些措施能够提高实验准确程度________。
A.选用两光学表面间距大的玻璃砖
B.选用两光学表面平行的玻璃砖
C.选用粗的大头针完成实验
D.插在玻璃砖同侧的两枚大头针间的距离尽量大些
(2)该小组用同一套器材完成了四次实验,记录的玻璃砖界线和四个大头针扎下的孔洞如下图所示,其中实验操作正确的是________。
(3)该小组选取了操作正确的实验记录,在白纸上画出光线的径迹,以入射点O为圆心作圆,与入射光线、折射光线分别交于A、B点,再过A、B点作法线NN′的垂线,垂足分别为C、D点,如图所示,则玻璃的折射率n=________。(用图中线段的字母表示)
答案 (1)AD (2)D (3)
解析 (1)测定玻璃折射率的关键是根据入射光线和出射光线确定在玻璃中的传播光线,因此选用两光学表面间距大的玻璃砖以及使同侧两枚大头针间的距离尽量大些都有利于提高实验的准确程度,A、D正确;两光学表面是否平行不影响折射率的测量,为减小误差,应选用细长的大头针,故B、C错误。
(2)两光学表面平行的玻璃砖的入射光线与出射光线平行,在空气中的入射角大于玻璃中的折射角,在题图中,根据玻璃砖界线及四个孔洞位置分别作出光路图及法线如图1所示,分析可知实验操作正确的是D。
(3)如图2所示,玻璃的折射率n=,又sini=,sinr=,故n=。
四、计算题
10.(2019·江苏高考)如图所示,某L形透明材料的折射率n=2。现沿AB方向切去一角,AB与水平方向的夹角为θ。为使水平方向的光线射到AB面时不会射入空气,求θ的最大值。
答案 60°
解析 光线射到AB面时不射入空气中,则在AB面发生全反射。当恰好发生全反射时,入射角为临界角C,此时θ最大,sinC=,由几何关系得C+θm=90°,解得θm=60°。
11.(2019·全国卷Ⅲ)如图,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°。一束光线平行于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出。
(1)求棱镜的折射率;
(2)保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光线射出。求此时AB边上入射角的正弦。
答案 (1) (2)
解析 (1)光路图及相关量如图所示。
光束在AB边上折射,由折射定律得=n①
式中n是棱镜的折射率,由几何关系可知
α+β=60°②
由几何关系和反射定律得β=β′=∠B③
联立①②③式,并代入i=60°得n=④
(2)设改变后的入射角为i′,折射角为α′,由折射定律得
=n⑤
依题意,光束在BC边上的入射角为全反射的临界角θc,且
sinθc=⑥
由几何关系得θc=α′+30°⑦
由④⑤⑥⑦式得入射角的正弦为sini′=。
12.(2019·全国卷Ⅰ)如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m。距水面4 m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin53°=0.8)。已知水的折射率为。
(1)求桅杆到P点的水平距离;
(2)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍照射在桅杆顶端,求船行驶的距离。
答案 (1)7 m (2)5.5 m
解析 (1)设光束从水面射出的点到桅杆的水平距离为x1,到P点的水平距离为x2;桅杆高度为h1,P点处水深为h2;激光束在水中与竖直方向的夹角为θ。由几何关系有
=tan53°①
=tanθ②
由折射定律有
sin53°=nsinθ③
设桅杆到P点的水平距离为x,则x=x1+x2④
联立①②③④式并代入题给数据得x=7 m⑤
(2)设激光束在水中与竖直方向的夹角为45°时,从水面出射的方向与竖直方向夹角为i′,由折射定律有
sini′=nsin45°⑥
设船向左行驶的距离为x′,此时光束从水面射出的点到桅杆的水平距离为x1′,到P点的水平距离为x2′,则
x1′+x2′=x′+x⑦
=tani′⑧
=tan45°⑨
联立⑤⑥⑦⑧⑨式并代入题给数据得
x′=(6-3) m≈5.5 m。
13.(2018·全国卷Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(1)求出射光相对于D点的入射光的偏角;
(2)为实现上述光路,棱镜折射率的取值应在什么范围?
答案 (1)60° (2)≤n<2
解析 (1)光线在BC边折射,由折射定律有
sini1=nsinr1①
式中,n为棱镜的折射率,i1和r1分别是该光线在BC边上的入射角和折射角。
光线在AC边上发生全反射,由反射定律有i2=r2②
式中i2和r2分别是该光线在AC边上的入射角和反射角。
光线在AB边上发生折射,由折射定律有nsini3=sinr3③
式中i3和r3分别是该光线在AB边上的入射角和折射角,
联立①②③式并结合几何关系得
i2=r2=60°,r1=i3=30°,i1=r3④
F点的出射光相对于D点的入射光的偏角为
δ=(r1-i1)+(180°-i2-r2)+(r3-i3)⑤
由④⑤式得δ=60°⑥
(2)光线在AC边上发生全反射,光线在AB边上不发生全反射,有i3式中C是全反射临界角,满足nsinC=1⑧
由④⑦⑧式知,棱镜的折射率n的取值范围应为≤n<2。
14.(2018·全国卷Ⅲ)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点作AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点作AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
答案
解析 过D点作AB边的垂线NN′交BC于N,连接OD,则∠ODN=α为来自O点的光线在D点的入射角;设该光线在D点的折射角为β,如图所示。
根据折射定律有nsinα=sinβ①
式中n为三棱镜的折射率
由几何关系可知β=60°②
∠EOF=30°③
在△OEF中有EF=OEsin∠EOF④
由③④式和题给条件得OE=2 cm⑤
根据⑤式和题给条件可知,△OED为等腰三角形,有
α=30°⑥
由①②⑥式得n=。
15.(2017·全国卷Ⅰ)如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R。已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
答案 1.43
解析 如图,根据光路的对称性和光路可逆性,与入射光线平行的出射光线一定与入射光线相对于OC轴对称,这样,从半球面射入的折射光线,将从圆柱体底面中心C点反射。
设入射光线在半球面的入射角为i,折射角为r,由折射定律有
sini=nsinr①
由正弦定理有=②
由几何关系,入射点的法线与OC的夹角为i,由题设条件和几何关系有sini=③
式中L是入射光线与OC的距离。
由②③式和题给数据得sinr=④
由①③④式和题给数据得n=≈1.43。
16.(2017·江苏高考)人的眼球可简化为如图所示的模型。折射率相同、半径不同的两个球体共轴。平行光束宽度为D,对称地沿轴线方向射入半径为R的小球,会聚在轴线上的P点。取球体的折射率为,且D=R。求光线的会聚角α。(示意图未按比例画出)
答案 30°
解析 如图所示,由几何关系sini=,解得i=45°
则由折射定律=n,解得r=30°
且i=r+,解得会聚角α=30°。
17.(2017·全国卷Ⅲ) 如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线)。已知玻璃的折射率为1.5。现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线)。求:
(1)从球面射出的光线对应的入射光线到光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离。
答案 (1)R (2)2.74R
解析 (1)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l。
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有
nsinic=1②
由几何关系有
sini=③
联立①②③式并利用题给条件,得l=R④
(2)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有
nsini1=sinr1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有
=⑥
由几何关系有
∠C=r1-i1⑦
sini1=⑧
联立⑤⑥⑦⑧式及题给条件得
OC=R≈2.74R。
18.(2017·全国卷Ⅱ) 一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
答案 1.55
解析 设从光源发出直接射到D点的光线的入射角为i1,折射角为r1。在剖面内作光源相对于反光壁的镜像对称点C,连接C、D,交反光壁于E点,由光源射向E点的光线,反射后沿ED射向D点,设此反射光线在D点的入射角为i2,折射角为r2,如图所示。
设该液体的折射率为n,由折射定律有
nsini1=sinr1①
nsini2=sinr2②
由题意知r1+r2=90°③
联立①②③式得n2=④
由几何关系可知sini1==⑤
sini2==⑥
联立④⑤⑥式得n≈1.55。
一、选择题
1.(2019·北京高考)利用图1所示的装置(示意图),观察光的干涉、衍射现象,在光屏上得到如图2中甲和乙两种图样。下列关于P处放置的光学元件说法正确的是( )
A.甲对应单缝,乙对应双缝
B.甲对应双缝,乙对应单缝
C.都是单缝,甲对应的缝宽较大
D.都是双缝,甲对应的双缝间距较大
答案 A
解析 单缝衍射图样的中央条纹亮且宽,相邻条纹间距不等;双缝干涉图样中相邻条纹间距相等。根据题目中给出的甲、乙两种图样可知,甲是单缝衍射的图样,乙是双缝干涉的图样,A正确。
2.(2018·北京高考)用双缝干涉实验装置得到白光的干涉条纹,在光源与单缝之间加上红色滤光片后( )
A.干涉条纹消失
B.彩色条纹中的红色条纹消失
C.中央条纹变成暗条纹
D.中央条纹变成红色
答案 D
解析 当用白光做干涉实验时,频率相同的色光,相互叠加干涉,在光屏上形成彩色条纹,中央为白色的亮条纹;当在光源与单缝之间加上红色滤光片后,只有红光能通过单缝,然后通过双缝后相互叠加干涉,在光屏上形成红、黑相间的干涉条纹,光屏中央为加强点,所以中央条纹变成红色亮条纹,A、B、C错误,D正确。
3.(2017·全国卷Ⅱ)(多选)在双缝干涉实验中,用绿色激光照射在双缝上,在缝后的屏幕上显示出干涉图样。若要增大干涉图样中两相邻亮条纹的间距,可选用的方法是( )
A.改用红色激光
B.改用蓝色激光
C.减小双缝间距
D.将屏幕向远离双缝的位置移动
E.将光源向远离双缝的位置移动
答案 ACD
解析 在双缝干涉实验中两相邻亮条纹的间距Δx=λ,因此要增大干涉图样中两相邻亮条纹的间距可减小双缝间的距离,增大屏幕与双缝的距离,换用波长更长或频率更小的光做光源,故选A、C、D。
4.(2017·北京高考) 如图所示,一束可见光穿过平行玻璃砖后,变为a、b两束单色光。如果光束b是蓝光,则光束a可能是( )
A.红光 B.黄光
C.绿光 D.紫光
答案 D
解析 解法一:光的偏折程度越大,则折射率越大,光的频率越大。题中a光的偏折程度大于b光的偏折程度,则玻璃对a光的折射率大于对b光的折射率,a光的频率大于b光的频率,只有D正确。
解法二:本题是单项选择,题中A、B、C光的频率均比蓝光的小,只有D光的频率比蓝光的大,可以直接判定D正确。
二、填空题
5.(2018·全国卷Ⅰ) 如图,△ABC为一玻璃三棱镜的横截面,∠A=30°。一束红光垂直AB边射入,从AC边上的D点射出,其折射角为60°,则玻璃对红光的折射率为________。若改用蓝光沿同一路径入射,则光线在D点射出时的折射角________(填“小于”“等于”或“大于”)60°。
答案 大于
解析 由光路可逆性,根据题述和图示可知,i=60°,r=30°,由折射定律,玻璃对红光的折射率n==。若改用蓝光沿同一路径入射,由于玻璃对蓝光的折射率大于玻璃对红光的折射率,则光线在D点射出时的折射角大于60°。
6.(2019·江苏高考)将两支铅笔并排放在一起,中间留一条狭缝,通过这条狭缝去看与其平行的日光灯,能观察到彩色条纹,这是由于光的________(选填“折射”“干涉”或“衍射”)。当缝的宽度________(选填“远大于”或“接近”)光波的波长时,这种现象十分明显。
答案 衍射 接近
解析 将两支铅笔并排放在一起,中间留一条狭缝,通过这条狭缝去看与其平行的日光灯,能观察到彩色条纹,这是由于光的衍射产生的;当缝的宽度与光波的波长接近或比光波的波长更小时,衍射现象很明显。
7.(2018·江苏高考)两束单色光A、B的波长分别为λA、λB,且λA>λB,则________(选填“A”或“B”)在水中发生全反射时的临界角较大。用同一装置进行杨氏双缝干涉实验时,可以观察到________(选填“A”或“B”)产生的条纹间距较大。
答案 A A
解析 波长越长,频率越小,折射率越小,根据临界角的正弦sinC=,可知波长越长临界角越大,所以A光在水中发生全反射时的临界角较大;双缝干涉条纹的间距Δx=λ,因为A光的波长较长,所以A光产生的条纹间距较大。
三、实验题
8.(2019·全国卷Ⅱ)某同学利用图示装置测量某种单色光的波长。实验时,接通电源使光源正常发光;调整光路,使得从目镜中可以观察到干涉条纹。回答下列问题:
(1)若想增加从目镜中观察到的条纹个数,该同学可________。
A.将单缝向双缝靠近
B.将屏向靠近双缝的方向移动
C.将屏向远离双缝的方向移动
D.使用间距更小的双缝
(2)若双缝的间距为d,屏与双缝间的距离为l,测得第1条暗条纹到第n条暗条纹之间的距离为Δx,则单色光的波长λ=________。
(3)某次测量时,选用的双缝的间距为0.300 mm,测得屏与双缝间的距离为1.20 m,第1条暗条纹到第4条暗条纹之间的距离为7.56 mm。则所测单色光的波长为________ nm(结果保留三位有效数字)。
答案 (1)B (2) (3)630
解析 (1)相邻明(暗)干涉条纹的间距Δx=λ,要增加观察到的条纹个数,即减小Δx,需增大d或减小l,因此应将屏向靠近双缝的方向移动,或使用间距更大的双缝,故A、C、D错误,B正确。
(2)第1条暗条纹到第n条暗条纹间的距离为Δx,则相邻暗条纹间的距离Δx′=,又Δx′=λ,解得λ=。
(3)由λ=,代入数据解得λ=630 nm。
9.(2019·天津高考)某小组做测定玻璃的折射率实验,所用器材有:玻璃砖,大头针,刻度尺,圆规,笔,白纸。
(1)下列哪些措施能够提高实验准确程度________。
A.选用两光学表面间距大的玻璃砖
B.选用两光学表面平行的玻璃砖
C.选用粗的大头针完成实验
D.插在玻璃砖同侧的两枚大头针间的距离尽量大些
(2)该小组用同一套器材完成了四次实验,记录的玻璃砖界线和四个大头针扎下的孔洞如下图所示,其中实验操作正确的是________。
(3)该小组选取了操作正确的实验记录,在白纸上画出光线的径迹,以入射点O为圆心作圆,与入射光线、折射光线分别交于A、B点,再过A、B点作法线NN′的垂线,垂足分别为C、D点,如图所示,则玻璃的折射率n=________。(用图中线段的字母表示)
答案 (1)AD (2)D (3)
解析 (1)测定玻璃折射率的关键是根据入射光线和出射光线确定在玻璃中的传播光线,因此选用两光学表面间距大的玻璃砖以及使同侧两枚大头针间的距离尽量大些都有利于提高实验的准确程度,A、D正确;两光学表面是否平行不影响折射率的测量,为减小误差,应选用细长的大头针,故B、C错误。
(2)两光学表面平行的玻璃砖的入射光线与出射光线平行,在空气中的入射角大于玻璃中的折射角,在题图中,根据玻璃砖界线及四个孔洞位置分别作出光路图及法线如图1所示,分析可知实验操作正确的是D。
(3)如图2所示,玻璃的折射率n=,又sini=,sinr=,故n=。
四、计算题
10.(2019·江苏高考)如图所示,某L形透明材料的折射率n=2。现沿AB方向切去一角,AB与水平方向的夹角为θ。为使水平方向的光线射到AB面时不会射入空气,求θ的最大值。
答案 60°
解析 光线射到AB面时不射入空气中,则在AB面发生全反射。当恰好发生全反射时,入射角为临界角C,此时θ最大,sinC=,由几何关系得C+θm=90°,解得θm=60°。
11.(2019·全国卷Ⅲ)如图,直角三角形ABC为一棱镜的横截面,∠A=90°,∠B=30°。一束光线平行于底边BC射到AB边上并进入棱镜,然后垂直于AC边射出。
(1)求棱镜的折射率;
(2)保持AB边上的入射点不变,逐渐减小入射角,直到BC边上恰好有光线射出。求此时AB边上入射角的正弦。
答案 (1) (2)
解析 (1)光路图及相关量如图所示。
光束在AB边上折射,由折射定律得=n①
式中n是棱镜的折射率,由几何关系可知
α+β=60°②
由几何关系和反射定律得β=β′=∠B③
联立①②③式,并代入i=60°得n=④
(2)设改变后的入射角为i′,折射角为α′,由折射定律得
=n⑤
依题意,光束在BC边上的入射角为全反射的临界角θc,且
sinθc=⑥
由几何关系得θc=α′+30°⑦
由④⑤⑥⑦式得入射角的正弦为sini′=。
12.(2019·全国卷Ⅰ)如图,一艘帆船静止在湖面上,帆船的竖直桅杆顶端高出水面3 m。距水面4 m的湖底P点发出的激光束,从水面出射后恰好照射到桅杆顶端,该出射光束与竖直方向的夹角为53°(取sin53°=0.8)。已知水的折射率为。
(1)求桅杆到P点的水平距离;
(2)船向左行驶一段距离后停止,调整由P点发出的激光束方向,当其与竖直方向夹角为45°时,从水面射出后仍照射在桅杆顶端,求船行驶的距离。
答案 (1)7 m (2)5.5 m
解析 (1)设光束从水面射出的点到桅杆的水平距离为x1,到P点的水平距离为x2;桅杆高度为h1,P点处水深为h2;激光束在水中与竖直方向的夹角为θ。由几何关系有
=tan53°①
=tanθ②
由折射定律有
sin53°=nsinθ③
设桅杆到P点的水平距离为x,则x=x1+x2④
联立①②③④式并代入题给数据得x=7 m⑤
(2)设激光束在水中与竖直方向的夹角为45°时,从水面出射的方向与竖直方向夹角为i′,由折射定律有
sini′=nsin45°⑥
设船向左行驶的距离为x′,此时光束从水面射出的点到桅杆的水平距离为x1′,到P点的水平距离为x2′,则
x1′+x2′=x′+x⑦
=tani′⑧
=tan45°⑨
联立⑤⑥⑦⑧⑨式并代入题给数据得
x′=(6-3) m≈5.5 m。
13.(2018·全国卷Ⅱ)如图,△ABC是一直角三棱镜的横截面,∠A=90°,∠B=60°,一细光束从BC边的D点折射后,射到AC边的E点,发生全反射后经AB边的F点射出。EG垂直于AC交BC于G,D恰好是CG的中点。不计多次反射。
(1)求出射光相对于D点的入射光的偏角;
(2)为实现上述光路,棱镜折射率的取值应在什么范围?
答案 (1)60° (2)≤n<2
解析 (1)光线在BC边折射,由折射定律有
sini1=nsinr1①
式中,n为棱镜的折射率,i1和r1分别是该光线在BC边上的入射角和折射角。
光线在AC边上发生全反射,由反射定律有i2=r2②
式中i2和r2分别是该光线在AC边上的入射角和反射角。
光线在AB边上发生折射,由折射定律有nsini3=sinr3③
式中i3和r3分别是该光线在AB边上的入射角和折射角,
联立①②③式并结合几何关系得
i2=r2=60°,r1=i3=30°,i1=r3④
F点的出射光相对于D点的入射光的偏角为
δ=(r1-i1)+(180°-i2-r2)+(r3-i3)⑤
由④⑤式得δ=60°⑥
(2)光线在AC边上发生全反射,光线在AB边上不发生全反射,有i3
由④⑦⑧式知,棱镜的折射率n的取值范围应为≤n<2。
14.(2018·全国卷Ⅲ)如图,某同学在一张水平放置的白纸上画了一个小标记“·”(图中O点),然后用横截面为等边三角形ABC的三棱镜压在这个标记上,小标记位于AC边上。D位于AB边上,过D点作AC边的垂线交AC于F。该同学在D点正上方向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点作AB边的垂线交直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的反射)
答案
解析 过D点作AB边的垂线NN′交BC于N,连接OD,则∠ODN=α为来自O点的光线在D点的入射角;设该光线在D点的折射角为β,如图所示。
根据折射定律有nsinα=sinβ①
式中n为三棱镜的折射率
由几何关系可知β=60°②
∠EOF=30°③
在△OEF中有EF=OEsin∠EOF④
由③④式和题给条件得OE=2 cm⑤
根据⑤式和题给条件可知,△OED为等腰三角形,有
α=30°⑥
由①②⑥式得n=。
15.(2017·全国卷Ⅰ)如图,一玻璃工件的上半部是半径为R的半球体,O点为球心;下半部是半径为R、高为2R的圆柱体,圆柱体底面镀有反射膜。有一平行于中心轴OC的光线从半球面射入,该光线与OC之间的距离为0.6R。已知最后从半球面射出的光线恰好与入射光线平行(不考虑多次反射)。求该玻璃的折射率。
答案 1.43
解析 如图,根据光路的对称性和光路可逆性,与入射光线平行的出射光线一定与入射光线相对于OC轴对称,这样,从半球面射入的折射光线,将从圆柱体底面中心C点反射。
设入射光线在半球面的入射角为i,折射角为r,由折射定律有
sini=nsinr①
由正弦定理有=②
由几何关系,入射点的法线与OC的夹角为i,由题设条件和几何关系有sini=③
式中L是入射光线与OC的距离。
由②③式和题给数据得sinr=④
由①③④式和题给数据得n=≈1.43。
16.(2017·江苏高考)人的眼球可简化为如图所示的模型。折射率相同、半径不同的两个球体共轴。平行光束宽度为D,对称地沿轴线方向射入半径为R的小球,会聚在轴线上的P点。取球体的折射率为,且D=R。求光线的会聚角α。(示意图未按比例画出)
答案 30°
解析 如图所示,由几何关系sini=,解得i=45°
则由折射定律=n,解得r=30°
且i=r+,解得会聚角α=30°。
17.(2017·全国卷Ⅲ) 如图,一半径为R的玻璃半球,O点是半球的球心,虚线OO′表示光轴(过球心O与半球底面垂直的直线)。已知玻璃的折射率为1.5。现有一束平行光垂直入射到半球的底面上,有些光线能从球面射出(不考虑被半球的内表面反射后的光线)。求:
(1)从球面射出的光线对应的入射光线到光轴距离的最大值;
(2)距光轴的入射光线经球面折射后与光轴的交点到O点的距离。
答案 (1)R (2)2.74R
解析 (1)如图,从底面上A处射入的光线,在球面上发生折射时的入射角为i,当i等于全反射临界角ic时,对应入射光线到光轴的距离最大,设最大距离为l。
i=ic①
设n是玻璃的折射率,由全反射临界角的定义有
nsinic=1②
由几何关系有
sini=③
联立①②③式并利用题给条件,得l=R④
(2)设与光轴相距的光线在球面B点发生折射时的入射角和折射角分别为i1和r1,由折射定律有
nsini1=sinr1⑤
设折射光线与光轴的交点为C,在△OBC中,由正弦定理有
=⑥
由几何关系有
∠C=r1-i1⑦
sini1=⑧
联立⑤⑥⑦⑧式及题给条件得
OC=R≈2.74R。
18.(2017·全国卷Ⅱ) 一直桶状容器的高为2l,底面是边长为l的正方形;容器内装满某种透明液体,过容器中心轴DD′、垂直于左右两侧面的剖面图如图所示。容器右侧内壁涂有反光材料,其他内壁涂有吸光材料。在剖面的左下角处有一点光源,已知由液体上表面的D点射出的两束光线相互垂直,求该液体的折射率。
答案 1.55
解析 设从光源发出直接射到D点的光线的入射角为i1,折射角为r1。在剖面内作光源相对于反光壁的镜像对称点C,连接C、D,交反光壁于E点,由光源射向E点的光线,反射后沿ED射向D点,设此反射光线在D点的入射角为i2,折射角为r2,如图所示。
设该液体的折射率为n,由折射定律有
nsini1=sinr1①
nsini2=sinr2②
由题意知r1+r2=90°③
联立①②③式得n2=④
由几何关系可知sini1==⑤
sini2==⑥
联立④⑤⑥式得n≈1.55。
