2019-2020学年苏科新版数学七年级上册《第6章 平面图形的认识(一)》单元测试卷(解析版)
文档属性
| 名称 | 2019-2020学年苏科新版数学七年级上册《第6章 平面图形的认识(一)》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 245.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 09:21:35 | ||
图片预览




文档简介
2019年苏科新版数学七年级上册《第6章 平面图形的认识(一)》单元测试卷
一.选择题(共15小题)
1.下列说法正确的是( )
A.过一点P只能作一条直线
B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线
D.射线a比直线b短
2.在墙壁上固定一根横放的木条,则至少需要( )枚钉子.
A.l B.2 C.3 D.随便多少枚
3.如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.两点确定一条线段
4.下列说法中,正确的有( )
①过两点有且只有一条直线,②连结两点的线段叫做两点的距离,
③两点之间,线段最短,④AB=BC,则点B是线段AC的中点.
A.4个 B.3个 C.2个 D.1个
5.已知线段AB=5,C是直线AB上一点,BC=2,则线段AC长为( )
A.7 B.3 C.3或7 D.以上都不对
6.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A. B.
C. D.
7.时钟显示为8:30时,时针与分针所夹的角是( )
A.90° B.120° C.75° D.84°
8.书店、学校、食堂在平面上分别用A、B、C来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC的度数应该是( )
A.65° B.35° C.165° D.135°
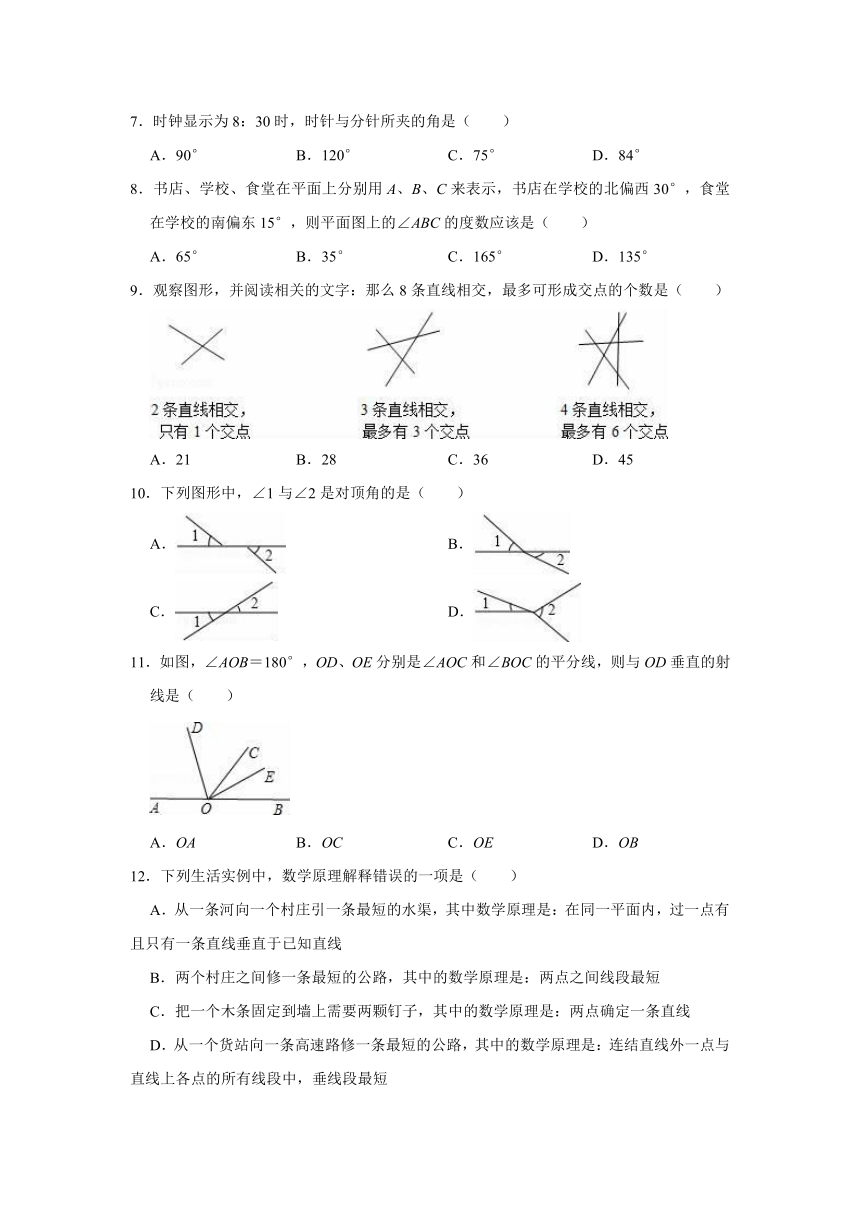
9.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A.21 B.28 C.36 D.45
10.下列图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
11.如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则与OD垂直的射线是( )
A.OA B.OC C.OE D.OB
12.下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短
13.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( )
A.线段PB的长是点P到直线a的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段PC的长是点C到直线PA的距离
14.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
15.已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是( )
A.相交 B.平行 C.垂直 D.平行或相交
二.填空题(共6小题)
16.如图,在直线I上顺次取A、B、C、D四点,则AC= +BC=AD﹣ ,AC+BD﹣BC= .
17.开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为 .
18.如图,把弯曲的河道改直,能够缩短航程,这样做的根据是 .
19.三条直线两两相交,则交点有 个.
20.如图,直线AB、CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD= 度.
21.如图,AB,CD相交于点O,OE⊥AB,垂足为O,∠COE=44°,则∠AOD= .
三.解答题(共3小题)
22.如图,平面上有A、B、C、D,4个点,根据下列语句画图.
(1)画线段AC、BD交于点F;
(2)连接AD,并将其反向延长;
(3)取一点P,使点P既在直线AB上又在直线CD上.
23.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
24.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
2019年苏科新版数学七年级上册《第6章 平面图形的认识(一)》单元测试卷
参考答案与试题解析
一.选择题(共15小题)
1.下列说法正确的是( )
A.过一点P只能作一条直线
B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线
D.射线a比直线b短
【分析】过一点可以做无数条直线,根据直线的表示方法,AB和BA是表示同一条直线.而射线AB和射线BA表示不同的射线,射线与直线不能进行长短的比较.
【解答】解:A、过一点P可以作无数条直线;故A错误.
B、直线可以用两个大写字母来表示,且直线没有方向,所以AB和BA是表示同一条直线;故B正确.
C、射线AB和射线BA,顶点不同,方向相反,故射线AB和射线BA表示不同的射线;故C错误.
D、射线和直线不能进行长短的比较;故D错误.
故选:B.
【点评】本题考查了直线,射线的表示方法,要能够区分直线与射线的不同点.
2.在墙壁上固定一根横放的木条,则至少需要( )枚钉子.
A.l B.2 C.3 D.随便多少枚
【分析】根据公理“两点确定一条直线”,来解答即可.
【解答】解:至少需要2根钉子.
故选:B.
【点评】解答此题不仅要根据公理,更要联系生活实际,以培养同学们的学以致用的思维习惯.
3.如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.两点确定一条线段
【分析】此题为数学知识的应用,由题意弯曲的河道改直,肯定为了尽量缩短两地之间的里程,就用到两点间线段最短定理.
【解答】解:因为两点之间线段最短,把弯曲的河道改直,能够缩短航程.
故选:C.
【点评】此题为数学知识的应用,考查知识点两点之间线段最短.
4.下列说法中,正确的有( )
①过两点有且只有一条直线,②连结两点的线段叫做两点的距离,
③两点之间,线段最短,④AB=BC,则点B是线段AC的中点.
A.4个 B.3个 C.2个 D.1个
【分析】根据直线的性质,线段的定性质,线段中点的定义,可得答案.
【解答】解:①过两点有且只有一条直线,故①符合题意;
②连接两点的线段的长度叫做两点的距离,故②不符合题意;
③两点之间,线段最短,故③符合题意;
④AB=BC,B在线段AC上,则点B是线段AC的中点,故④不符合题意;
故选:C.
【点评】本题考查了两点间的距离,利用直线的性质,线段的定性质,线段中点的定义是解题关键,注意线段是几何图形,两点间的距离是线段的长度.
5.已知线段AB=5,C是直线AB上一点,BC=2,则线段AC长为( )
A.7 B.3 C.3或7 D.以上都不对
【分析】C在直线AB上应分:在线段AB上或在线段AB延长线上两种情况讨论.
【解答】解:当点C在线段AB上时:AC=5﹣2=3;当C在AB的延长线上时:AC=5+2=7.
故选:C.
【点评】本题要注意点C在直线AB上,要分几种情况讨论.
6.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A. B.
C. D.
【分析】根据角的四种表示方法和具体要求回答即可.
【解答】解:A、以O为顶点的角不止一个,不能用∠O表示,故A选项错误;
B、以O为顶点的角不止一个,不能用∠O表示,故B选项错误;
C、以O为顶点的角不止一个,不能用∠O表示,故C选项错误;
D、能用∠1,∠AOB,∠O三种方法表示同一个角,故D选项正确.
故选:D.
【点评】本题考查了角的表示方法的应用,掌握角的表示方法是解题的关键.
7.时钟显示为8:30时,时针与分针所夹的角是( )
A.90° B.120° C.75° D.84°
【分析】由于钟面被分成12大格,每格为30°,而8点30分时,钟面上时针指向数字8与9的中间,分针指向数字6,则它们所夹的角为2×30°+×30°.
【解答】解:8点30分时,钟面上时针指向数字8与9的中间,分针指向数字6,
所以时针与分针所成的角等于2×30°+×30°=75°.
故选:C.
【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动()°,并且利用起点时间时针和分针的位置关系建立角的图形.
8.书店、学校、食堂在平面上分别用A、B、C来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC的度数应该是( )
A.65° B.35° C.165° D.135°
【分析】首先根据叙述作出A、B、C的相对位置,然后根据角度的和差计算即可.
【解答】解:∠ABD=90°﹣30°=60°,
则∠ABC=60°+90°+15°=165°.
故选:C.
【点评】本题考查了方向角的定义,理解方向角的定义,作出A、B、C的相对位置是解决本题的关键.
9.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A.21 B.28 C.36 D.45
【分析】解答此题的关键是观察图形找出规律,如果8条直线相交,那么每条直线最多可形成7个交点.然后即可得出答案.
【解答】解:观察图形可得:
n条直线相交最多可形成的交点个数为,
∴8条直线相交,最多可形成交点的个数为====28.
故选:B.
【点评】此题主要考查学生对相交线的理解和掌握.解答此题的关键是观察图形找出规律.
10.下列图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角进行分析即可.
【解答】解:A、∠1与∠2不是对顶角,故此选项错误;
B、∠1与∠2不是对顶角,故此选项错误;
C、∠1与∠2是对顶角,故此选项正确;
D、∠1与∠2不是对顶角,故此选项错误;
故选:C.
【点评】此题主要考查了对顶角,关键是掌握对顶角定义.
11.如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则与OD垂直的射线是( )
A.OA B.OC C.OE D.OB
【分析】由图可知,∠AOC和∠BOC是邻补角,它们的角平分线OD,OE相互垂直.
【解答】解:∵∠AOC+∠BOC=∠AOB=180°,
OD,OE分别是∠AOC和∠BOC的平分线,
∴∠DOC+∠COE=(∠AOC+∠BOC)=90°.
∴与OD垂直的射线是OE.
故选:C.
【点评】此题主要考查了垂线的定义即:当两条直线相交所成的四个角中,有一个角是直角时,即两条直线互相垂直.
12.下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短
【分析】根据垂线段最短、直线和线段的性质即可得到结论.
【解答】解:A、从一条河向一个村庄引一条最短的水渠,其中数学原理是:垂线段最短,故原命题错误;
B、两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短,正确;
C、一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线,正确;
D、从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短,正确.
故选:A.
【点评】本题考查了垂线段最短,直线和线段的性质,熟练掌握各性质是解题的关键.
13.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( )
A.线段PB的长是点P到直线a的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段PC的长是点C到直线PA的距离
【分析】利用点到直线的距离的定义、垂线段最短分析.
【解答】解:A、根据点到直线的距离的定义:即点到这一直线的垂线段的长度.故此选项正确;
B、根据垂线段最短可知此选项正确;
C、线段AP的长是点A到直线PC的距离,故选项错误;
D、根据点到直线的距离即点到这一直线的垂线段的长度.故此选项正确.
故选:C.
【点评】本题主要考查了点到直线的距离的定义,及垂线段最短的性质.
14.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
【分析】①根据两点之间线段最短判断.
②对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
③根据平行公理进行判断.
④根据垂线的性质进行判断.
⑤距离是指的长度.
⑥根据在同一平面内,两条不重合的直线的位置关系.
【解答】解:①两点之间的所有连线中,线段最短,故①正确.
②相等的角不一定是对顶角,故②错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④错误.
⑤两点之间的距离是两点间的线段的长度,故⑤错误.
⑥在同一平面内,两直线的位置关系只有两种:相交和平行,故⑥正确.
综上所述,正确的结论有2个.
故选:B.
【点评】本题主要考查对平行线的定义,两点间的距离,相交线等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
15.已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是( )
A.相交 B.平行 C.垂直 D.平行或相交
【分析】根据平行公理的推论直接判断直线c与直线a的位置关系即可.
【解答】解:∵在同一平面内,直线a∥b,直线b∥c,
∴直线c与直线a的位置关系是:a∥c.
故选:B.
【点评】此题主要考查了平行公理的推论,熟练记忆推论内容是解题关键.
二.填空题(共6小题)
16.如图,在直线I上顺次取A、B、C、D四点,则AC= AB +BC=AD﹣ CD ,AC+BD﹣BC= AD .
【分析】首先画出直线找出4个点,然后找出线段的关系.
【解答】解:由线段的关系可知AC=AB+BC=AD﹣CD,
AC+BD﹣BC=AD.
【点评】本题主要考查直线、线段、射线的知识点,不是很难.
17.开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为 两点确定一条直线 .
【分析】根据直线的确定方法,易得答案.
【解答】解:根据两点确定一条直线.
故答案为:两点确定一条直线.
【点评】本题考查直线的确定:两点确定一条直线.
18.如图,把弯曲的河道改直,能够缩短航程,这样做的根据是 两点之间线段最短 .
【分析】根据两点之间线段最短即可得出答案.
【解答】解:由两点之间线段最短可知,把弯曲的河道改直,能够缩短航程,这样做根据的道理是两点之间线段最短,
故答案为:两点之间线段最短.
【点评】本题考查了线段的性质,属于概念题,关键是掌握两点之间线段最短.
19.三条直线两两相交,则交点有 1或3 个.
【分析】三条直线两两相交有两种情况,即三条直线不过同一个交点时有三个交点;三条直线过同一个交点时有一个交点.
【解答】解:如图所示:
故三条直线两两相交,则交点有1或3个.
故答案为:1或3.
【点评】本题考查的是三条直线两两相交的情况,解答此类题目的关键是画出图形,找出可能出现的情况再进行解答.
20.如图,直线AB、CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD= 35 度.
【分析】由OE与AB垂直,利用垂直的定义得到∠AOE=90°,由∠AOE﹣∠COE求出∠AOC的度数,再利用对顶角相等即可求出∠BOD的度数.
【解答】解:∵OE⊥AB,∴∠AOE=90°,
∵∠COE=55°,
∴∠AOC=∠AOE﹣∠COE=35°,
则∠BOD=∠AOC=35°.
故答案为:35
【点评】此题考查了对顶角、邻补角,以及垂线,熟练掌握对顶角相等是解本题的关键.
21.如图,AB,CD相交于点O,OE⊥AB,垂足为O,∠COE=44°,则∠AOD= 134° .
【分析】首先根据垂直定义可得∠EOB=90°,再根据角的和差关系可得∠COB=134°,再根据对顶角相等可得∠AOD的度数.
【解答】解:∵OE⊥AB,
∴∠EOB=90°,
∵∠COE=44°,
∴∠COB=90°+44°=134°,
∴∠AOD=134°,
故答案为:134°.
【点评】此题主要考查了垂线以及对顶角,关键是算出∠EOB的度数,掌握对顶角相等.
三.解答题(共3小题)
22.如图,平面上有A、B、C、D,4个点,根据下列语句画图.
(1)画线段AC、BD交于点F;
(2)连接AD,并将其反向延长;
(3)取一点P,使点P既在直线AB上又在直线CD上.
【分析】根据题意要求,然后作图即可,注意作图的规范性.
【解答】解:所画图形如下:
【点评】本题考查作图的知识,难度不大,解答此题,要熟悉直线、射线、线段的概念,并熟悉基本工具的用法.
23.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
【分析】因为教学楼和图书馆处于同一条直线上,两点之间线段最短;连接AB,使AB两点同在一条直线上,与河流的交点既是最佳位置.
【解答】解:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短;
情景二:(需画出图形,并标明P点位置)
理由:两点之间的所有连线中,线段最短.
赞同情景二中运用知识的做法.应用数学知识为人类服务时应注意应用数学不能以破坏环境为代价.
【点评】此题为数学知识的应用,考查知识点两点之间线段最短.
24.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ∠BOD ,∠BOE的邻补角为 ∠AOE ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
【分析】(1)利用对顶角、邻补角的定义直接回答即可;
(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
【解答】解:(1)∠AOC的对顶角为∠BOD,∠BOE的邻补角为∠AOE;
(2)∵∠DOB=∠AOC=70°,∠DOB=∠BOE+∠EOD及∠BOE:∠EOD=2:3,
∴得,
∴,
∴∠BOE=28°,
∴∠AOE=180°﹣∠BOE=152°.
【点评】本题主要考查了对顶角,邻补角的定义,利用对顶角相等的性质和互为邻补角的两个角的和等于180°求解.
一.选择题(共15小题)
1.下列说法正确的是( )
A.过一点P只能作一条直线
B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线
D.射线a比直线b短
2.在墙壁上固定一根横放的木条,则至少需要( )枚钉子.
A.l B.2 C.3 D.随便多少枚
3.如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.两点确定一条线段
4.下列说法中,正确的有( )
①过两点有且只有一条直线,②连结两点的线段叫做两点的距离,
③两点之间,线段最短,④AB=BC,则点B是线段AC的中点.
A.4个 B.3个 C.2个 D.1个
5.已知线段AB=5,C是直线AB上一点,BC=2,则线段AC长为( )
A.7 B.3 C.3或7 D.以上都不对
6.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A. B.
C. D.
7.时钟显示为8:30时,时针与分针所夹的角是( )
A.90° B.120° C.75° D.84°
8.书店、学校、食堂在平面上分别用A、B、C来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC的度数应该是( )
A.65° B.35° C.165° D.135°
9.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A.21 B.28 C.36 D.45
10.下列图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
11.如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则与OD垂直的射线是( )
A.OA B.OC C.OE D.OB
12.下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短
13.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( )
A.线段PB的长是点P到直线a的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段PC的长是点C到直线PA的距离
14.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
15.已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是( )
A.相交 B.平行 C.垂直 D.平行或相交
二.填空题(共6小题)
16.如图,在直线I上顺次取A、B、C、D四点,则AC= +BC=AD﹣ ,AC+BD﹣BC= .
17.开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为 .
18.如图,把弯曲的河道改直,能够缩短航程,这样做的根据是 .
19.三条直线两两相交,则交点有 个.
20.如图,直线AB、CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD= 度.
21.如图,AB,CD相交于点O,OE⊥AB,垂足为O,∠COE=44°,则∠AOD= .
三.解答题(共3小题)
22.如图,平面上有A、B、C、D,4个点,根据下列语句画图.
(1)画线段AC、BD交于点F;
(2)连接AD,并将其反向延长;
(3)取一点P,使点P既在直线AB上又在直线CD上.
23.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
24.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
2019年苏科新版数学七年级上册《第6章 平面图形的认识(一)》单元测试卷
参考答案与试题解析
一.选择题(共15小题)
1.下列说法正确的是( )
A.过一点P只能作一条直线
B.直线AB和直线BA表示同一条直线
C.射线AB和射线BA表示同一条射线
D.射线a比直线b短
【分析】过一点可以做无数条直线,根据直线的表示方法,AB和BA是表示同一条直线.而射线AB和射线BA表示不同的射线,射线与直线不能进行长短的比较.
【解答】解:A、过一点P可以作无数条直线;故A错误.
B、直线可以用两个大写字母来表示,且直线没有方向,所以AB和BA是表示同一条直线;故B正确.
C、射线AB和射线BA,顶点不同,方向相反,故射线AB和射线BA表示不同的射线;故C错误.
D、射线和直线不能进行长短的比较;故D错误.
故选:B.
【点评】本题考查了直线,射线的表示方法,要能够区分直线与射线的不同点.
2.在墙壁上固定一根横放的木条,则至少需要( )枚钉子.
A.l B.2 C.3 D.随便多少枚
【分析】根据公理“两点确定一条直线”,来解答即可.
【解答】解:至少需要2根钉子.
故选:B.
【点评】解答此题不仅要根据公理,更要联系生活实际,以培养同学们的学以致用的思维习惯.
3.如图,把弯曲的河道改直,能够缩短航程.这样做根据的道理是( )
A.两点之间,直线最短 B.两点确定一条直线
C.两点之间,线段最短 D.两点确定一条线段
【分析】此题为数学知识的应用,由题意弯曲的河道改直,肯定为了尽量缩短两地之间的里程,就用到两点间线段最短定理.
【解答】解:因为两点之间线段最短,把弯曲的河道改直,能够缩短航程.
故选:C.
【点评】此题为数学知识的应用,考查知识点两点之间线段最短.
4.下列说法中,正确的有( )
①过两点有且只有一条直线,②连结两点的线段叫做两点的距离,
③两点之间,线段最短,④AB=BC,则点B是线段AC的中点.
A.4个 B.3个 C.2个 D.1个
【分析】根据直线的性质,线段的定性质,线段中点的定义,可得答案.
【解答】解:①过两点有且只有一条直线,故①符合题意;
②连接两点的线段的长度叫做两点的距离,故②不符合题意;
③两点之间,线段最短,故③符合题意;
④AB=BC,B在线段AC上,则点B是线段AC的中点,故④不符合题意;
故选:C.
【点评】本题考查了两点间的距离,利用直线的性质,线段的定性质,线段中点的定义是解题关键,注意线段是几何图形,两点间的距离是线段的长度.
5.已知线段AB=5,C是直线AB上一点,BC=2,则线段AC长为( )
A.7 B.3 C.3或7 D.以上都不对
【分析】C在直线AB上应分:在线段AB上或在线段AB延长线上两种情况讨论.
【解答】解:当点C在线段AB上时:AC=5﹣2=3;当C在AB的延长线上时:AC=5+2=7.
故选:C.
【点评】本题要注意点C在直线AB上,要分几种情况讨论.
6.如图,能用∠AOB,∠O,∠1三种方法表示同一个角的图形是( )
A. B.
C. D.
【分析】根据角的四种表示方法和具体要求回答即可.
【解答】解:A、以O为顶点的角不止一个,不能用∠O表示,故A选项错误;
B、以O为顶点的角不止一个,不能用∠O表示,故B选项错误;
C、以O为顶点的角不止一个,不能用∠O表示,故C选项错误;
D、能用∠1,∠AOB,∠O三种方法表示同一个角,故D选项正确.
故选:D.
【点评】本题考查了角的表示方法的应用,掌握角的表示方法是解题的关键.
7.时钟显示为8:30时,时针与分针所夹的角是( )
A.90° B.120° C.75° D.84°
【分析】由于钟面被分成12大格,每格为30°,而8点30分时,钟面上时针指向数字8与9的中间,分针指向数字6,则它们所夹的角为2×30°+×30°.
【解答】解:8点30分时,钟面上时针指向数字8与9的中间,分针指向数字6,
所以时针与分针所成的角等于2×30°+×30°=75°.
故选:C.
【点评】本题考查钟表时针与分针的夹角.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动()°,并且利用起点时间时针和分针的位置关系建立角的图形.
8.书店、学校、食堂在平面上分别用A、B、C来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC的度数应该是( )
A.65° B.35° C.165° D.135°
【分析】首先根据叙述作出A、B、C的相对位置,然后根据角度的和差计算即可.
【解答】解:∠ABD=90°﹣30°=60°,
则∠ABC=60°+90°+15°=165°.
故选:C.
【点评】本题考查了方向角的定义,理解方向角的定义,作出A、B、C的相对位置是解决本题的关键.
9.观察图形,并阅读相关的文字:那么8条直线相交,最多可形成交点的个数是( )
A.21 B.28 C.36 D.45
【分析】解答此题的关键是观察图形找出规律,如果8条直线相交,那么每条直线最多可形成7个交点.然后即可得出答案.
【解答】解:观察图形可得:
n条直线相交最多可形成的交点个数为,
∴8条直线相交,最多可形成交点的个数为====28.
故选:B.
【点评】此题主要考查学生对相交线的理解和掌握.解答此题的关键是观察图形找出规律.
10.下列图形中,∠1与∠2是对顶角的是( )
A. B.
C. D.
【分析】根据对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角进行分析即可.
【解答】解:A、∠1与∠2不是对顶角,故此选项错误;
B、∠1与∠2不是对顶角,故此选项错误;
C、∠1与∠2是对顶角,故此选项正确;
D、∠1与∠2不是对顶角,故此选项错误;
故选:C.
【点评】此题主要考查了对顶角,关键是掌握对顶角定义.
11.如图,∠AOB=180°,OD、OE分别是∠AOC和∠BOC的平分线,则与OD垂直的射线是( )
A.OA B.OC C.OE D.OB
【分析】由图可知,∠AOC和∠BOC是邻补角,它们的角平分线OD,OE相互垂直.
【解答】解:∵∠AOC+∠BOC=∠AOB=180°,
OD,OE分别是∠AOC和∠BOC的平分线,
∴∠DOC+∠COE=(∠AOC+∠BOC)=90°.
∴与OD垂直的射线是OE.
故选:C.
【点评】此题主要考查了垂线的定义即:当两条直线相交所成的四个角中,有一个角是直角时,即两条直线互相垂直.
12.下列生活实例中,数学原理解释错误的一项是( )
A.从一条河向一个村庄引一条最短的水渠,其中数学原理是:在同一平面内,过一点有且只有一条直线垂直于已知直线
B.两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短
C.把一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线
D.从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短
【分析】根据垂线段最短、直线和线段的性质即可得到结论.
【解答】解:A、从一条河向一个村庄引一条最短的水渠,其中数学原理是:垂线段最短,故原命题错误;
B、两个村庄之间修一条最短的公路,其中的数学原理是:两点之间线段最短,正确;
C、一个木条固定到墙上需要两颗钉子,其中的数学原理是:两点确定一条直线,正确;
D、从一个货站向一条高速路修一条最短的公路,其中的数学原理是:连结直线外一点与直线上各点的所有线段中,垂线段最短,正确.
故选:A.
【点评】本题考查了垂线段最短,直线和线段的性质,熟练掌握各性质是解题的关键.
13.如图,点P是直线a外的一点,点A、B、C在直线a上,且PB⊥a,垂足是B,PA⊥PC,则下列不正确的语句是( )
A.线段PB的长是点P到直线a的距离
B.PA、PB、PC三条线段中,PB最短
C.线段AC的长是点A到直线PC的距离
D.线段PC的长是点C到直线PA的距离
【分析】利用点到直线的距离的定义、垂线段最短分析.
【解答】解:A、根据点到直线的距离的定义:即点到这一直线的垂线段的长度.故此选项正确;
B、根据垂线段最短可知此选项正确;
C、线段AP的长是点A到直线PC的距离,故选项错误;
D、根据点到直线的距离即点到这一直线的垂线段的长度.故此选项正确.
故选:C.
【点评】本题主要考查了点到直线的距离的定义,及垂线段最短的性质.
14.下列说法正确的有( )
①两点之间的所有连线中,线段最短;
②相等的角叫对顶角;
③过一点有且只有一条直线与已知直线平行;
④过一点有且只有一条直线与已知直线垂直;
⑤两点之间的距离是两点间的线段;
⑥在同一平面内的两直线位置关系只有两种:平行或相交.
A.1个 B.2个 C.3个 D.4个
【分析】①根据两点之间线段最短判断.
②对顶角:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.
③根据平行公理进行判断.
④根据垂线的性质进行判断.
⑤距离是指的长度.
⑥根据在同一平面内,两条不重合的直线的位置关系.
【解答】解:①两点之间的所有连线中,线段最短,故①正确.
②相等的角不一定是对顶角,故②错误.
③经过直线外一点有且只有一条直线与已知直线平行,故③错误.
④同一平面内,过一点有且只有一条直线与已知直线垂直,故④错误.
⑤两点之间的距离是两点间的线段的长度,故⑤错误.
⑥在同一平面内,两直线的位置关系只有两种:相交和平行,故⑥正确.
综上所述,正确的结论有2个.
故选:B.
【点评】本题主要考查对平行线的定义,两点间的距离,相交线等知识点的理解和掌握,能熟练地运用性质进行说理是解此题的关键.
15.已知在同一平面内,有三条直线a,b,c,若a∥b,b∥c,则直线a与直线c之间的位置关系是( )
A.相交 B.平行 C.垂直 D.平行或相交
【分析】根据平行公理的推论直接判断直线c与直线a的位置关系即可.
【解答】解:∵在同一平面内,直线a∥b,直线b∥c,
∴直线c与直线a的位置关系是:a∥c.
故选:B.
【点评】此题主要考查了平行公理的推论,熟练记忆推论内容是解题关键.
二.填空题(共6小题)
16.如图,在直线I上顺次取A、B、C、D四点,则AC= AB +BC=AD﹣ CD ,AC+BD﹣BC= AD .
【分析】首先画出直线找出4个点,然后找出线段的关系.
【解答】解:由线段的关系可知AC=AB+BC=AD﹣CD,
AC+BD﹣BC=AD.
【点评】本题主要考查直线、线段、射线的知识点,不是很难.
17.开学整理教室时,老师总是先把每一列最前和最后的课桌摆好,然后再依次摆中间的课桌,一会儿一列课桌摆在一条线上,整整齐齐,这是因为 两点确定一条直线 .
【分析】根据直线的确定方法,易得答案.
【解答】解:根据两点确定一条直线.
故答案为:两点确定一条直线.
【点评】本题考查直线的确定:两点确定一条直线.
18.如图,把弯曲的河道改直,能够缩短航程,这样做的根据是 两点之间线段最短 .
【分析】根据两点之间线段最短即可得出答案.
【解答】解:由两点之间线段最短可知,把弯曲的河道改直,能够缩短航程,这样做根据的道理是两点之间线段最短,
故答案为:两点之间线段最短.
【点评】本题考查了线段的性质,属于概念题,关键是掌握两点之间线段最短.
19.三条直线两两相交,则交点有 1或3 个.
【分析】三条直线两两相交有两种情况,即三条直线不过同一个交点时有三个交点;三条直线过同一个交点时有一个交点.
【解答】解:如图所示:
故三条直线两两相交,则交点有1或3个.
故答案为:1或3.
【点评】本题考查的是三条直线两两相交的情况,解答此类题目的关键是画出图形,找出可能出现的情况再进行解答.
20.如图,直线AB、CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD= 35 度.
【分析】由OE与AB垂直,利用垂直的定义得到∠AOE=90°,由∠AOE﹣∠COE求出∠AOC的度数,再利用对顶角相等即可求出∠BOD的度数.
【解答】解:∵OE⊥AB,∴∠AOE=90°,
∵∠COE=55°,
∴∠AOC=∠AOE﹣∠COE=35°,
则∠BOD=∠AOC=35°.
故答案为:35
【点评】此题考查了对顶角、邻补角,以及垂线,熟练掌握对顶角相等是解本题的关键.
21.如图,AB,CD相交于点O,OE⊥AB,垂足为O,∠COE=44°,则∠AOD= 134° .
【分析】首先根据垂直定义可得∠EOB=90°,再根据角的和差关系可得∠COB=134°,再根据对顶角相等可得∠AOD的度数.
【解答】解:∵OE⊥AB,
∴∠EOB=90°,
∵∠COE=44°,
∴∠COB=90°+44°=134°,
∴∠AOD=134°,
故答案为:134°.
【点评】此题主要考查了垂线以及对顶角,关键是算出∠EOB的度数,掌握对顶角相等.
三.解答题(共3小题)
22.如图,平面上有A、B、C、D,4个点,根据下列语句画图.
(1)画线段AC、BD交于点F;
(2)连接AD,并将其反向延长;
(3)取一点P,使点P既在直线AB上又在直线CD上.
【分析】根据题意要求,然后作图即可,注意作图的规范性.
【解答】解:所画图形如下:
【点评】本题考查作图的知识,难度不大,解答此题,要熟悉直线、射线、线段的概念,并熟悉基本工具的用法.
23.知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.
情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:
你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
【分析】因为教学楼和图书馆处于同一条直线上,两点之间线段最短;连接AB,使AB两点同在一条直线上,与河流的交点既是最佳位置.
【解答】解:情景一:因为教学楼和图书馆处于同一条直线上,两点之间的所有连线中,线段最短;
情景二:(需画出图形,并标明P点位置)
理由:两点之间的所有连线中,线段最短.
赞同情景二中运用知识的做法.应用数学知识为人类服务时应注意应用数学不能以破坏环境为代价.
【点评】此题为数学知识的应用,考查知识点两点之间线段最短.
24.如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ∠BOD ,∠BOE的邻补角为 ∠AOE ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.
【分析】(1)利用对顶角、邻补角的定义直接回答即可;
(2)根据对顶角相等求出∠BOD的度数,再根据∠BOE:∠EOD=2:3求出∠BOE的度数,然后利用互为邻补角的两个角的和等于180°即可求出∠AOE的度数.
【解答】解:(1)∠AOC的对顶角为∠BOD,∠BOE的邻补角为∠AOE;
(2)∵∠DOB=∠AOC=70°,∠DOB=∠BOE+∠EOD及∠BOE:∠EOD=2:3,
∴得,
∴,
∴∠BOE=28°,
∴∠AOE=180°﹣∠BOE=152°.
【点评】本题主要考查了对顶角,邻补角的定义,利用对顶角相等的性质和互为邻补角的两个角的和等于180°求解.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
