2020届北师大版数学九年级下册第三章教学课件:3.6.1 切线的性质(共16张PPT)
文档属性
| 名称 | 2020届北师大版数学九年级下册第三章教学课件:3.6.1 切线的性质(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 906.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 21:55:46 | ||
图片预览






文档简介
(共16张PPT)
第三章
圆
3.6.1 切线的性质
教学目标
1.理解直线与圆有三种位置关系,并能利用公共点的个数,圆心到直线的距离与半径之间的关系来判定它们.
2.掌握直线与圆相切的判断方法和如何作出直线与圆相切,并能利用公共点的个数和圆心到直线的距离与半径之间的关系来判定.
新课导入
情境引入
太阳与地平线的位置关系,列车的轮子与铁轨之间的关系, 给你留下了_________的位置关系的印象.
直线与圆
新课导入
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,试说出直线和圆有几种位置关系?
直线和圆有两个公共点
直线和圆有一个公共点
直线和圆没有公共点
探究:
新课导入
直线和圆的位置关系:
l
l
l
?
?
?
直线和圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切.这条直线叫做圆的切线.唯一的公共点叫切点.
直线和圆没有公共点时,叫做直线和圆相离.
o
o
o
M
新知探究
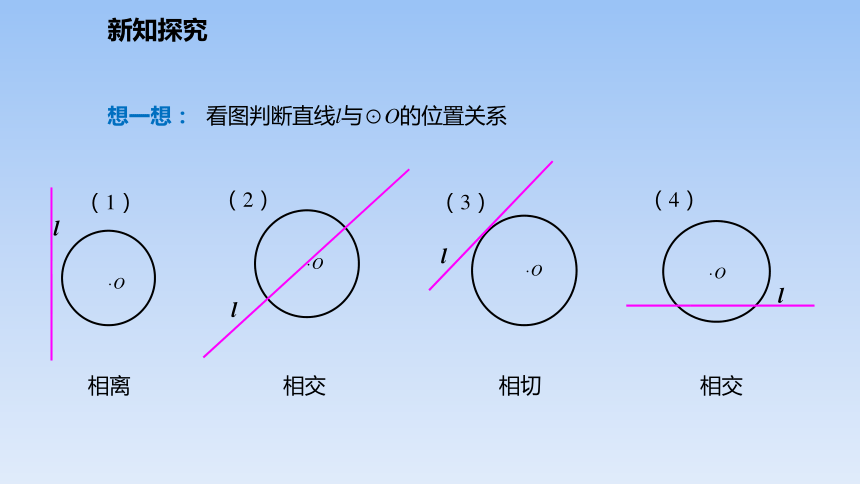
看图判断直线l与⊙O的位置关系
(1)
(2)
(3)
(4)
相离
相切
相交
相交
l
l
l
l
·O
·O
·O
·O
想一想:
新知探究
利用公共点的个数判断直线和圆的位置关系具有一定的局限,你有更好的判断方法吗?
“点和圆的位置关系”怎样判断?
新知探究
点和圆的三种位置关系:
A
A
A
?
?
?
?
?
?
o
o
o
点在圆外
点在圆上
点在圆内
d>r
d=r
d仿照这种方法怎样判断“直线和圆的位置关系”?
图形 点与圆的位置关系 圆心到点的距离d与半径r的关系
新知探究
2.直线和圆相切
d = r
3.直线和圆相交
d < r
1.直线和圆相离
d > r
直线和圆的位置关系
令圆心O到直线l的距离为d,圆的半径为r .
探究新知:
新知探究
1.已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .
2.直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .
d>5
r>8
3.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( )
A.相离 B.相交
C.相切 D.相切或相交
C
巩固练习:
新知探究
提示:求圆心A到x轴、y轴的距离各是多少.
A.(-3,-4)
O
4.已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是______.
B
C
4
3
相离
相切
新知探究
5.已知Rt△ABC的斜边AB=8cm, AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
新知探究
当r=4cm时,d当r=2cm时,d>r,AB与⊙C相离;
解 : (1)过点C作CD⊥AB于点D.
∵AB=8cm,AC=4cm.
∴∠A=60°.
┛
D
课堂小结
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质, 的关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
直线与圆位置关系的判定可以从数的角度和形的角度进行判定,数的
角度是圆心到直线的距离;形的角度是直线与圆的交点的个数.
圆的切线垂直于过切点的半径.
规律方法:
课堂小测
1.如图,在Rt△ABC中,∠C = 90°,∠B = 30°,BC = 4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
B
课堂小测
2. 在平面直角坐标系中,以点(3,2)为圆心、3为半径的圆,一定( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
C
第三章
圆
3.6.1 切线的性质
教学目标
1.理解直线与圆有三种位置关系,并能利用公共点的个数,圆心到直线的距离与半径之间的关系来判定它们.
2.掌握直线与圆相切的判断方法和如何作出直线与圆相切,并能利用公共点的个数和圆心到直线的距离与半径之间的关系来判定.
新课导入
情境引入
太阳与地平线的位置关系,列车的轮子与铁轨之间的关系, 给你留下了_________的位置关系的印象.
直线与圆
新课导入
作一个圆,把直尺边缘看成一条直线.固定圆,平移直尺,试说出直线和圆有几种位置关系?
直线和圆有两个公共点
直线和圆有一个公共点
直线和圆没有公共点
探究:
新课导入
直线和圆的位置关系:
l
l
l
?
?
?
直线和圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线
直线和圆有唯一公共点时,叫做直线和圆相切.这条直线叫做圆的切线.唯一的公共点叫切点.
直线和圆没有公共点时,叫做直线和圆相离.
o
o
o
M
新知探究
看图判断直线l与⊙O的位置关系
(1)
(2)
(3)
(4)
相离
相切
相交
相交
l
l
l
l
·O
·O
·O
·O
想一想:
新知探究
利用公共点的个数判断直线和圆的位置关系具有一定的局限,你有更好的判断方法吗?
“点和圆的位置关系”怎样判断?
新知探究
点和圆的三种位置关系:
A
A
A
?
?
?
?
?
?
o
o
o
点在圆外
点在圆上
点在圆内
d>r
d=r
d
图形 点与圆的位置关系 圆心到点的距离d与半径r的关系
新知探究
2.直线和圆相切
d = r
3.直线和圆相交
d < r
1.直线和圆相离
d > r
直线和圆的位置关系
令圆心O到直线l的距离为d,圆的半径为r .
探究新知:
新知探究
1.已知圆的半径等于5,直线l与圆没有交点,则圆心到直线的距离d的取值范围是 .
2.直线l与半径为r的⊙O相交,且点O到直线l的距离为8,则r的取值范围是 .
d>5
r>8
3.圆心O到直线的距离等于⊙O的半径,则直线和⊙O的位置关系是( )
A.相离 B.相交
C.相切 D.相切或相交
C
巩固练习:
新知探究
提示:求圆心A到x轴、y轴的距离各是多少.
A.(-3,-4)
O
4.已知⊙A的直径为6,点A的坐标为(-3,-4),则x轴与⊙A的位置关系是_____, y轴与⊙A的位置关系是______.
B
C
4
3
相离
相切
新知探究
5.已知Rt△ABC的斜边AB=8cm, AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,AB与⊙C相切?
(2)以点C为圆心,分别以2cm和4cm的长为半径作两个圆,这两个圆与AB分别有怎样的位置关系?
新知探究
当r=4cm时,d
解 : (1)过点C作CD⊥AB于点D.
∵AB=8cm,AC=4cm.
∴∠A=60°.
┛
D
课堂小结
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质, 的关系来判断.
在实际应用中,常采用第二种方法判定.
两
直线与圆的公共点
圆心到直线的距离d与半径r
直线与圆位置关系的判定可以从数的角度和形的角度进行判定,数的
角度是圆心到直线的距离;形的角度是直线与圆的交点的个数.
圆的切线垂直于过切点的半径.
规律方法:
课堂小测
1.如图,在Rt△ABC中,∠C = 90°,∠B = 30°,BC = 4 cm,以点C为圆心,以2 cm的长为半径作圆,则⊙C与AB的位置关系是( )
A.相离 B.相切
C.相交 D.相切或相交
B
课堂小测
2. 在平面直角坐标系中,以点(3,2)为圆心、3为半径的圆,一定( )
A.与x轴相切,与y轴相切
B.与x轴相切,与y轴相交
C.与x轴相交,与y轴相切
D.与x轴相交,与y轴相交
C
