第一章《集合与函数概念》期末复习 课件(共30张PPT)
文档属性
| 名称 | 第一章《集合与函数概念》期末复习 课件(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 10:05:30 | ||
图片预览









文档简介
(共30张PPT)
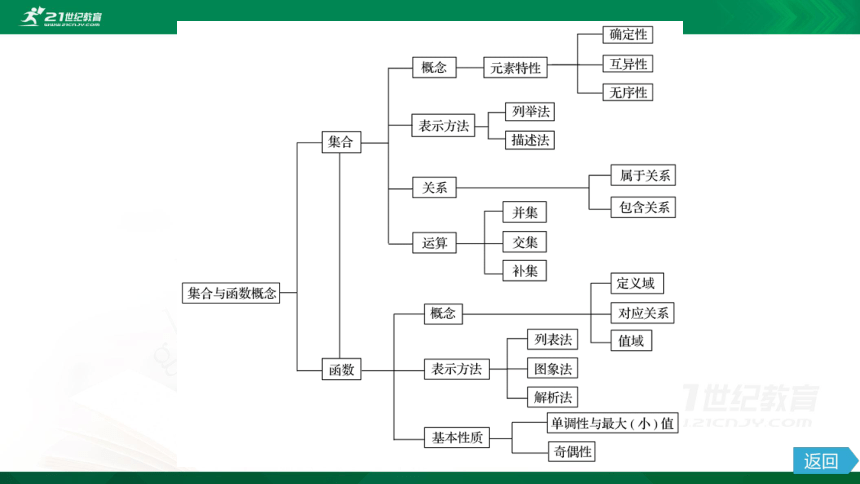
第一章 集合与函数概念
NEIRONGSUOYIN
内容索引
知识网络
考点突破
达标检测
1
知识网络
PART ONE
2
考点突破
PART TWO
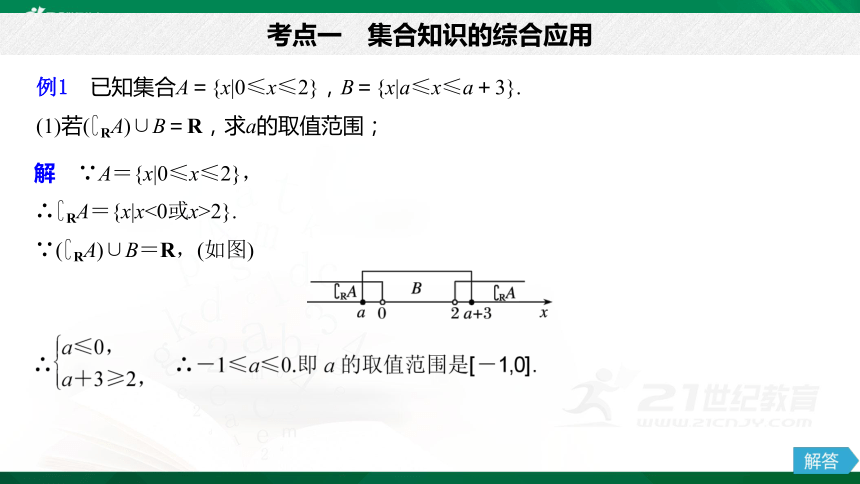
例1 已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若(?RA)∪B=R,求a的取值范围;
考点一 集合知识的综合应用
解 ∵A={x|0≤x≤2},
∴?RA={x|x<0或x>2}.
∵(?RA)∪B=R,(如图)
(2)是否存在a使(?RA)∪B=R且A∩B=??
解 由(1)知当(?RA)∪B=R时,
-1≤a≤0,而a+3∈[2,3],
则A?B,这与A∩B=?矛盾.
即这样的a不存在.
借助数轴表达集合间的关系可以更直观,但操作时要规范,如区间端点的顺序、虚实不能标反.
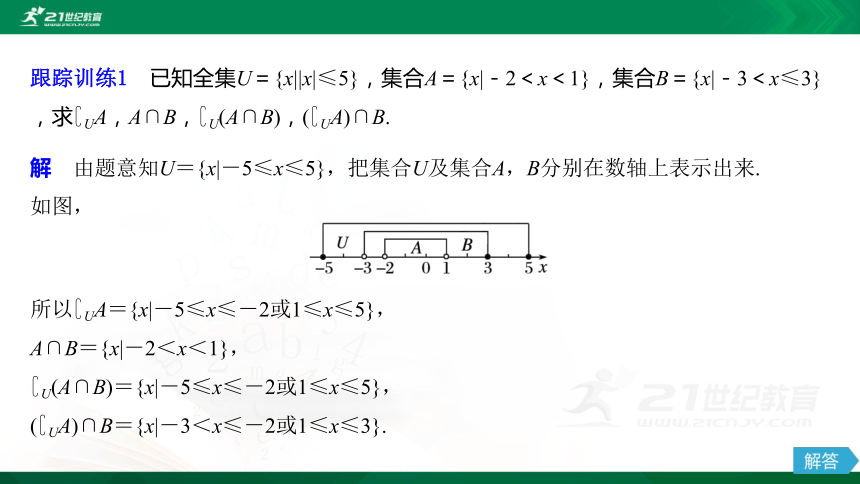
跟踪训练1 已知全集U={x||x|≤5},集合A={x|-2<x<1},集合B={x|-3<x≤3},求?UA,A∩B,?U(A∩B),(?UA)∩B.
解 由题意知U={x|-5≤x≤5},把集合U及集合A,B分别在数轴上表示出来.
如图,
所以?UA={x|-5≤x≤-2或1≤x≤5},
A∩B={x|-2<x<1},
?U(A∩B)={x|-5≤x≤-2或1≤x≤5},
(?UA)∩B={x|-3<x≤-2或1≤x≤3}.
考点二 抽象函数的单调性与奇偶性问题
命题角度1 抽象函数的奇偶性的判断
例2 若定义在R上的函数f(x)满足:对任意的x,y∈R,恒有f(x+y)=f(x)+f(y)+1,
求证:f(x)+1为奇函数.
多维探究
证明 令x=y=0,则f(0)=2f(0)+1,
所以f(0)=-1,
令y=-x,则f(0)=f(x)+f(-x)+1,
即-1=f(x)+f(-x)+1,
所以f(x)+1=-f(-x)-1
=-[f(-x)+1],所以f(x)+1为奇函数.
抽象函数奇偶性的判断,关键是通过赋值探究f(x)与f(-x)的关系.
跟踪训练2 已知函数f(x)不为0,当x,y∈R时,恒有f(x+y)+f(x-y)=2f(x)·f(y).
求证:f(x)是偶函数.
证明 令x=y=0,
则f(0)+f(0)=2f(0)·f(0),
又f(0)≠0,
∴f(0)=1.
令x=0,y∈R,
则f(y)+f(-y)=2f(0)·f(y)=2f(y),
∴f(y)=f(-y),
∴f(x)是偶函数.
命题角度2 抽象函数的单调性的判断
例3 已知定义在区间(0,+∞)上的函数f(x)满足f =f(x)-f(y),且当x>1时,f(x)<0.
(1)求f(1)的值;
解 令y=x,
则f(1)=f(x)-f(x)=0.
(2)判断f(x)的单调性.
解 设x1,x2∈(0,+∞)且x1∴f(x1)>f(x2),
∴f(x)在(0,+∞)上是单调递减函数.
抽象函数单调性的判断,是根据条件合理赋值,转化成函数单调性定义的形式.其关键是合理赋值.
跟踪训练3 设函数f(x)对任意实数x,y都有f(x+y)=f(x)+f(y),且x>0时,f(x)<0,f(1)=-2.
(1)求证:f(x)是奇函数;
证明 令x=y=0,
则f(0)=f(0)+f(0),
∴f(0)=0.
令y=-x,
则f(0)=f(x)+f(-x),即f(x)=-f(-x),
∴f(x)是奇函数.
(2)求f(x)在[-3,3]上的最大值与最小值.
解 设x1,x2∈R且x1则x2-x1>0,
∴f(x2-x1)<0.
令x=x2,y=-x1,
则f(x2-x1)=f(x2)+f(-x1)
=f(x2)-f(x1)<0,
∴f(x1)>f(x2),
∴f(x)是R上的单调减函数,
∴f(x)max=f(-3)=-f(3)=-3f(1)=6,
f(x)min=f(3)=-f(-3)=-6.
考点三 函数性质的综合应用
例4 已知函数f(x)是定义在区间[-1,1]上的奇函数,且f(1)=1,若对于任意的m,n∈[-1,1]有 >0.
(1)判断函数的单调性(不要求证明);
解 函数f(x)在区间[-1,1]上是增函数.
(2)解不等式f解 由(1)知函数f(x)在区间[-1,1]上是增函数,
(3)若f(x)≤-2at+2对于任意的x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围.
解 因为函数f(x)在区间[-1,1]上是增函数,且f(1)=1,
要使得对于任意的x∈[-1,1],a∈[-1,1]都有f(x)≤-2at+2恒成立,只需对任意的a∈[-1,1],-2at+2≥1恒成立.
令y=-2at+1,此时y可以看作a的一次函数,且在a∈[-1,1]时,y≥0恒成立.
(1)解决有关函数性质的综合应用问题的通法就是根据函数的奇偶性解答或作出图象辅助解答,先证明函数的单调性,再由单调性求最值.
(2)研究抽象函数的性质时要紧扣其定义,同时注意根据解题需要给x灵活赋值.
解 ∵f(x)是奇函数,∴f(-x)=-f(x),
(1)求实数m和n的值;
比较得n=-n,n=0.
∴实数m和n的值分别是2和0.
(2)求函数f(x)在区间[-2,-1]上的最值.
任取x1,x2∈[-2,-1],且x1∵-2≤x1∴x1-x2<0,x1x2>1,x1x2-1>0,
∴f(x1)-f(x2)<0,即f(x1)∴函数f(x)在[-2,-1]上为增函数.
3
达标检测
PART THREE
A.P=Q B.P?Q
C.P?Q D.P∩Q=?
1
2
3
4
5
√
所以Q?P.
2.下列函数中,满足“f(x+y)=f(x)+f(y)”的单调递增函数是
A.f(x)=x2(x≥0) B.f(x)=-2x
C.f(x)=3x D.f(x)=x3
1
2
3
4
5
√
1
2
3
4
5
3.设函数f(x),g(x)的定义域为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是
A.f(x)g(x)是偶函数
B.|f(x)|g(x)是奇函数
C.f(x)|g(x)|是奇函数
D.|f(x)g(x)|是奇函数
√
解析 f(-x)|g(-x)|=[-f(x)]|g(x)|
=-f(x)|g(x)|.
4.若f(x)是偶函数,其定义域为(-∞,+∞),且在[0,+∞)上是减函数,设 f? =m,f? =n,则m,n的大小关系是_______.
1
2
3
4
5
m≥n
又f(x)在[0,+∞)上是减函数,
1
2
3
4
5
5.已知函数y= 的图象与函数y=kx-2的图象恰有两个交点,则实数k的取值范
围是____________.
(0,1)∪(1,4)
解析 根据绝对值的意义,
在平面直角坐标系中作出该函数的图象,如图所示.
根据图象可知,当0谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第一章 集合与函数概念
NEIRONGSUOYIN
内容索引
知识网络
考点突破
达标检测
1
知识网络
PART ONE
2
考点突破
PART TWO
例1 已知集合A={x|0≤x≤2},B={x|a≤x≤a+3}.
(1)若(?RA)∪B=R,求a的取值范围;
考点一 集合知识的综合应用
解 ∵A={x|0≤x≤2},
∴?RA={x|x<0或x>2}.
∵(?RA)∪B=R,(如图)
(2)是否存在a使(?RA)∪B=R且A∩B=??
解 由(1)知当(?RA)∪B=R时,
-1≤a≤0,而a+3∈[2,3],
则A?B,这与A∩B=?矛盾.
即这样的a不存在.
借助数轴表达集合间的关系可以更直观,但操作时要规范,如区间端点的顺序、虚实不能标反.
跟踪训练1 已知全集U={x||x|≤5},集合A={x|-2<x<1},集合B={x|-3<x≤3},求?UA,A∩B,?U(A∩B),(?UA)∩B.
解 由题意知U={x|-5≤x≤5},把集合U及集合A,B分别在数轴上表示出来.
如图,
所以?UA={x|-5≤x≤-2或1≤x≤5},
A∩B={x|-2<x<1},
?U(A∩B)={x|-5≤x≤-2或1≤x≤5},
(?UA)∩B={x|-3<x≤-2或1≤x≤3}.
考点二 抽象函数的单调性与奇偶性问题
命题角度1 抽象函数的奇偶性的判断
例2 若定义在R上的函数f(x)满足:对任意的x,y∈R,恒有f(x+y)=f(x)+f(y)+1,
求证:f(x)+1为奇函数.
多维探究
证明 令x=y=0,则f(0)=2f(0)+1,
所以f(0)=-1,
令y=-x,则f(0)=f(x)+f(-x)+1,
即-1=f(x)+f(-x)+1,
所以f(x)+1=-f(-x)-1
=-[f(-x)+1],所以f(x)+1为奇函数.
抽象函数奇偶性的判断,关键是通过赋值探究f(x)与f(-x)的关系.
跟踪训练2 已知函数f(x)不为0,当x,y∈R时,恒有f(x+y)+f(x-y)=2f(x)·f(y).
求证:f(x)是偶函数.
证明 令x=y=0,
则f(0)+f(0)=2f(0)·f(0),
又f(0)≠0,
∴f(0)=1.
令x=0,y∈R,
则f(y)+f(-y)=2f(0)·f(y)=2f(y),
∴f(y)=f(-y),
∴f(x)是偶函数.
命题角度2 抽象函数的单调性的判断
例3 已知定义在区间(0,+∞)上的函数f(x)满足f =f(x)-f(y),且当x>1时,f(x)<0.
(1)求f(1)的值;
解 令y=x,
则f(1)=f(x)-f(x)=0.
(2)判断f(x)的单调性.
解 设x1,x2∈(0,+∞)且x1
∴f(x)在(0,+∞)上是单调递减函数.
抽象函数单调性的判断,是根据条件合理赋值,转化成函数单调性定义的形式.其关键是合理赋值.
跟踪训练3 设函数f(x)对任意实数x,y都有f(x+y)=f(x)+f(y),且x>0时,f(x)<0,f(1)=-2.
(1)求证:f(x)是奇函数;
证明 令x=y=0,
则f(0)=f(0)+f(0),
∴f(0)=0.
令y=-x,
则f(0)=f(x)+f(-x),即f(x)=-f(-x),
∴f(x)是奇函数.
(2)求f(x)在[-3,3]上的最大值与最小值.
解 设x1,x2∈R且x1
∴f(x2-x1)<0.
令x=x2,y=-x1,
则f(x2-x1)=f(x2)+f(-x1)
=f(x2)-f(x1)<0,
∴f(x1)>f(x2),
∴f(x)是R上的单调减函数,
∴f(x)max=f(-3)=-f(3)=-3f(1)=6,
f(x)min=f(3)=-f(-3)=-6.
考点三 函数性质的综合应用
例4 已知函数f(x)是定义在区间[-1,1]上的奇函数,且f(1)=1,若对于任意的m,n∈[-1,1]有 >0.
(1)判断函数的单调性(不要求证明);
解 函数f(x)在区间[-1,1]上是增函数.
(2)解不等式f
(3)若f(x)≤-2at+2对于任意的x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围.
解 因为函数f(x)在区间[-1,1]上是增函数,且f(1)=1,
要使得对于任意的x∈[-1,1],a∈[-1,1]都有f(x)≤-2at+2恒成立,只需对任意的a∈[-1,1],-2at+2≥1恒成立.
令y=-2at+1,此时y可以看作a的一次函数,且在a∈[-1,1]时,y≥0恒成立.
(1)解决有关函数性质的综合应用问题的通法就是根据函数的奇偶性解答或作出图象辅助解答,先证明函数的单调性,再由单调性求最值.
(2)研究抽象函数的性质时要紧扣其定义,同时注意根据解题需要给x灵活赋值.
解 ∵f(x)是奇函数,∴f(-x)=-f(x),
(1)求实数m和n的值;
比较得n=-n,n=0.
∴实数m和n的值分别是2和0.
(2)求函数f(x)在区间[-2,-1]上的最值.
任取x1,x2∈[-2,-1],且x1
∴f(x1)-f(x2)<0,即f(x1)
3
达标检测
PART THREE
A.P=Q B.P?Q
C.P?Q D.P∩Q=?
1
2
3
4
5
√
所以Q?P.
2.下列函数中,满足“f(x+y)=f(x)+f(y)”的单调递增函数是
A.f(x)=x2(x≥0) B.f(x)=-2x
C.f(x)=3x D.f(x)=x3
1
2
3
4
5
√
1
2
3
4
5
3.设函数f(x),g(x)的定义域为R,且f(x)是奇函数,g(x)是偶函数,则下列结论中正确的是
A.f(x)g(x)是偶函数
B.|f(x)|g(x)是奇函数
C.f(x)|g(x)|是奇函数
D.|f(x)g(x)|是奇函数
√
解析 f(-x)|g(-x)|=[-f(x)]|g(x)|
=-f(x)|g(x)|.
4.若f(x)是偶函数,其定义域为(-∞,+∞),且在[0,+∞)上是减函数,设 f? =m,f? =n,则m,n的大小关系是_______.
1
2
3
4
5
m≥n
又f(x)在[0,+∞)上是减函数,
1
2
3
4
5
5.已知函数y= 的图象与函数y=kx-2的图象恰有两个交点,则实数k的取值范
围是____________.
(0,1)∪(1,4)
解析 根据绝对值的意义,
在平面直角坐标系中作出该函数的图象,如图所示.
根据图象可知,当0
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
