人教版八年级数学第十九章一次函数:19.1.1 变量与函数(第2课时) (共18张PPT)
文档属性
| 名称 | 人教版八年级数学第十九章一次函数:19.1.1 变量与函数(第2课时) (共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 166.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 20:18:51 | ||
图片预览





文档简介
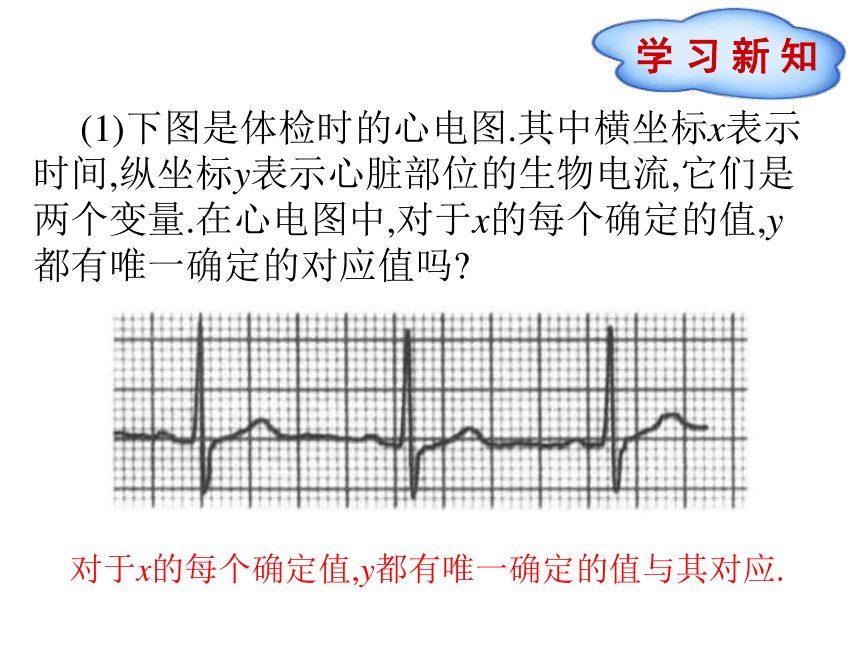
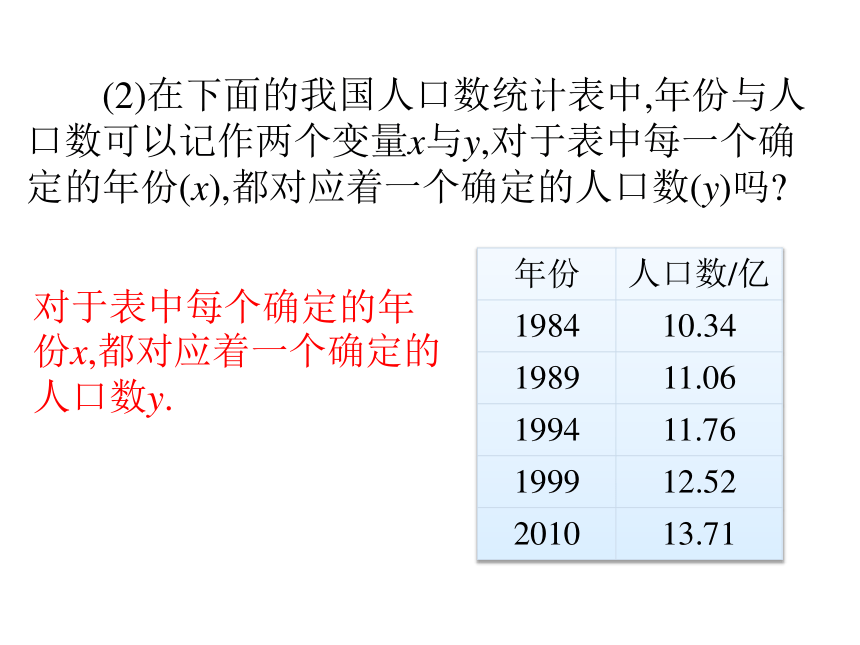
课件18张PPT。八年级数学·下 新课标[人]第十九章 一次函数19.1.1 变量与函数 (第2课时)想一想 你听说过“两个铁球同时落地”的故事吗?站在比萨斜塔顶部,让两个铁球自由下落,在铁球下落的过程中,随着时间的变化,铁球下落的速度是怎样变化的?铁球下落的速度v随下落的时间t的变化而变化.这就是我们今天要继续学习的内容. (1)下图是体检时的心电图.其中横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每个确定的值,y都有唯一确定的对应值吗?对于x的每个确定值,y都有唯一确定的值与其对应. (2)在下面的我国人口数统计表中,年份与人口数可以记作两个变量x与y,对于表中每一个确定的年份(x),都对应着一个确定的人口数(y)吗?对于表中每个确定的年份x,都对应着一个确定的人口数y. 小结 一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.如果当x=a时,y=b,那么b叫做当自变量的值为a时的函数值.知识拓展 (1)当已知函数解析式时,给出自变量的值,求相应函数值,就是将自变量x的值代入函数解析式,求代数式的值. (2)当已知函数解析式时,给出函数值,求相应自变量x的值,就是解方程. (3)已知函数解析式,当自变量确定时,函数值也唯一确定;当函数值确定时,自变量不一定唯一确定. 例:(教材例1)汽车油箱中有汽油50 L. 如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1 L/km.
(1)写出表示y与x的函数关系的式子;解:行驶路程x是自变量,油箱中的油量y是x的函数,
它们的关系为y=50-0.1x.(2)指出自变量x的取值范围. 解:仅从式子y=50-0.1x看,x可以取任意实数. 但是考虑到x代表的实际意义为行驶路程,因此x不能取负数.行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即0.1x≤50.
因此,自变量x的取值范围是0≤x≤500. (3)汽车行驶200 km时,油箱中还有多少汽油?解:汽车行驶200 km时,油箱中的汽油量是函数y=50-0.1x 在x=200时的函数值.
将x=200代入y=50-0.1x,得y=50-0.1×200=30.
故汽车行驶200 km时,油箱中还有30 L汽油. [归纳总结] 当函数关系式表示实际问题时,自变量的取值必须使实际问题有意义. 例:(补充) 求下列函数中自变量x的取值范围. (1)y=3x-1;(2)y=2x2+7;解: x为任意实数.解:根据题意,得x+2≠0,则x≠-2.解: x为任意实数.解: 根据题意,得x-2≥0,则x≥2. 含分式的函数,自变量的取值范围应满足的条件是:分母不为0;含二次根式的函数,自变量的取值范围应满足的条件是:被开方数为非负数;既含分式又含二次根式的函数,自变量的取值范围应满足的条件是:分母不为0且被开方数为非负数.归纳总结 解析式 在例1中,像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式. (1)在变化过程中有两个变量x,y,如果对于x的取值范围内的每一个确定的值y都有唯一的值和它对应,那么就说y是x的函数,x是自变量. (2)函数解析式中自变量的取值范围必须使函数解析式有意义.可分为下列几种情况: 解析式 ①当函数解析式是整式时,自变量的取值范围是全体实数. ②当函数解析式是分式(分母中含有字母)时,自变量的取值范围要使分母不为零. ③当函数解析式是偶次根式时,自变量的取值范围必须使被开方数是非负数. ④在实际问题中,自变量的取值范围除使函数解析式有意义外,还要使实际问题有意义. ⑤自变量的取值范围可以是有限或无限的,也可以是几个数或单独的一个数. 函数解析式是等式,指明了哪个是自变量,哪个是函数,书写函数解析式是有顺序的.例如y=x-4表示y是x的函数;若x=y+5,则表示x是y的函数,也就是说求y关于x的函数解析式,必须用含自变量x的代数式表示y,即等式的左边是一个变量y,右边是一个含x的代数式.解析 1.在变化过程中有两个变量x,y,如果对于x的取值范围内的每一个确定的值y都有唯一的值和它对应,那么就说y是x的函数,x是自变量.课堂小结课堂小结 2.函数解析式中自变量的取值范围必须使函数解析式有意义.
(1)当函数解析式是整式时,自变量的取值范围是全体实数.
(2)当函数解析式是分式(分母中含有字母)时,自变量的取值范围要使分母不为零.
(3)当函数解析式是偶次根式时,自变量的取值范围必须使被开方数是非负数.
(4)在实际问题中,自变量的取值范围除使函数解析式有意义外,还要使实际问题有意义. 1.下表表示y与x的函数关系,则此函数的解析式为 .?解析:根据表格中的数据知:y是x的一半的相反
数,故y=-0.5x.故填y=-0.5x.y=0.5x 2.自来水的收费标准是每月不超过10吨,每吨水1.2元,超过部分每吨水1.8元,小王家5月份用水x吨(x>10),应交水费y元,则y与x的函数关系式为 .?解析:小王家的水费=10吨的水费+超过10吨部分的水费.即y=10×1.2+1.8(x-10)=12+1.8x-18=1.8x-6.故填y=1.8x-6.y=1.8x-63.甲车速度为20米/秒,乙车速度为25米/秒.现甲车在乙车前面500米,设x秒后两车之间的距离为y米.求y随x(0≤x≤100)变化的函数解析式.解:由题意可知x秒后两车行驶路程分别是:
甲车为20x米,乙车为25x米.
两车行驶路程差为25x-20x=5x(米),
两车之间距离为(500-5x)米,
所以y随x变化的函数关系式为
y=500-5x(0≤x≤100).
(1)写出表示y与x的函数关系的式子;解:行驶路程x是自变量,油箱中的油量y是x的函数,
它们的关系为y=50-0.1x.(2)指出自变量x的取值范围. 解:仅从式子y=50-0.1x看,x可以取任意实数. 但是考虑到x代表的实际意义为行驶路程,因此x不能取负数.行驶中的耗油量为0.1x,它不能超过油箱中现有汽油量50,即0.1x≤50.
因此,自变量x的取值范围是0≤x≤500. (3)汽车行驶200 km时,油箱中还有多少汽油?解:汽车行驶200 km时,油箱中的汽油量是函数y=50-0.1x 在x=200时的函数值.
将x=200代入y=50-0.1x,得y=50-0.1×200=30.
故汽车行驶200 km时,油箱中还有30 L汽油. [归纳总结] 当函数关系式表示实际问题时,自变量的取值必须使实际问题有意义. 例:(补充) 求下列函数中自变量x的取值范围. (1)y=3x-1;(2)y=2x2+7;解: x为任意实数.解:根据题意,得x+2≠0,则x≠-2.解: x为任意实数.解: 根据题意,得x-2≥0,则x≥2. 含分式的函数,自变量的取值范围应满足的条件是:分母不为0;含二次根式的函数,自变量的取值范围应满足的条件是:被开方数为非负数;既含分式又含二次根式的函数,自变量的取值范围应满足的条件是:分母不为0且被开方数为非负数.归纳总结 解析式 在例1中,像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式. (1)在变化过程中有两个变量x,y,如果对于x的取值范围内的每一个确定的值y都有唯一的值和它对应,那么就说y是x的函数,x是自变量. (2)函数解析式中自变量的取值范围必须使函数解析式有意义.可分为下列几种情况: 解析式 ①当函数解析式是整式时,自变量的取值范围是全体实数. ②当函数解析式是分式(分母中含有字母)时,自变量的取值范围要使分母不为零. ③当函数解析式是偶次根式时,自变量的取值范围必须使被开方数是非负数. ④在实际问题中,自变量的取值范围除使函数解析式有意义外,还要使实际问题有意义. ⑤自变量的取值范围可以是有限或无限的,也可以是几个数或单独的一个数. 函数解析式是等式,指明了哪个是自变量,哪个是函数,书写函数解析式是有顺序的.例如y=x-4表示y是x的函数;若x=y+5,则表示x是y的函数,也就是说求y关于x的函数解析式,必须用含自变量x的代数式表示y,即等式的左边是一个变量y,右边是一个含x的代数式.解析 1.在变化过程中有两个变量x,y,如果对于x的取值范围内的每一个确定的值y都有唯一的值和它对应,那么就说y是x的函数,x是自变量.课堂小结课堂小结 2.函数解析式中自变量的取值范围必须使函数解析式有意义.
(1)当函数解析式是整式时,自变量的取值范围是全体实数.
(2)当函数解析式是分式(分母中含有字母)时,自变量的取值范围要使分母不为零.
(3)当函数解析式是偶次根式时,自变量的取值范围必须使被开方数是非负数.
(4)在实际问题中,自变量的取值范围除使函数解析式有意义外,还要使实际问题有意义. 1.下表表示y与x的函数关系,则此函数的解析式为 .?解析:根据表格中的数据知:y是x的一半的相反
数,故y=-0.5x.故填y=-0.5x.y=0.5x 2.自来水的收费标准是每月不超过10吨,每吨水1.2元,超过部分每吨水1.8元,小王家5月份用水x吨(x>10),应交水费y元,则y与x的函数关系式为 .?解析:小王家的水费=10吨的水费+超过10吨部分的水费.即y=10×1.2+1.8(x-10)=12+1.8x-18=1.8x-6.故填y=1.8x-6.y=1.8x-63.甲车速度为20米/秒,乙车速度为25米/秒.现甲车在乙车前面500米,设x秒后两车之间的距离为y米.求y随x(0≤x≤100)变化的函数解析式.解:由题意可知x秒后两车行驶路程分别是:
甲车为20x米,乙车为25x米.
两车行驶路程差为25x-20x=5x(米),
两车之间距离为(500-5x)米,
所以y随x变化的函数关系式为
y=500-5x(0≤x≤100).
