人教版必修1 第四章牛顿运动定律-专题:牛顿第二定律瞬时性问题(共16张PPT)
文档属性
| 名称 | 人教版必修1 第四章牛顿运动定律-专题:牛顿第二定律瞬时性问题(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 174.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-26 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
牛顿运动定律运用之
瞬时性问题专题
一、瞬时性问题
(1)物体运动的加速度a与其所受的合外力F有瞬时对应关系,所谓瞬时性,就是物体的加速度与其所受的合外力有瞬时对应的关系,每一瞬时的加速度只取决于这一瞬时的合外力。也就是物体一旦受到不为零的合外力的作用,物体立即产生加速度;当合外力的方向、大小改变时,物体的加速度方向、大小也立即发生相应的改变;当物体的合外力为零时,物体的加速度也立即为零。由此可知,力和加速度之间是瞬时对应的。(物体运动的加速度可以突变)。
二、突变类问题(力的瞬时性)
(2)A. 刚性绳(或接触面)一旦不发生明显形变就能产生弹力的物体,剪断(或脱离)后,弹力立即消失或改变,不需要形变恢复时间,在瞬时问题中,其弹力可以突变,成为零或者别的值。一般题目中所给的细线、轻杆和接触面在不加特殊说明时,均可按此模型处理。
(3)B. 轻弹簧(或橡皮绳)发生明显形变,需要较长的形变恢复时间,在瞬时问题中其弹力不能突变,大小方向均不变。
二、突变类问题(力的瞬时性)
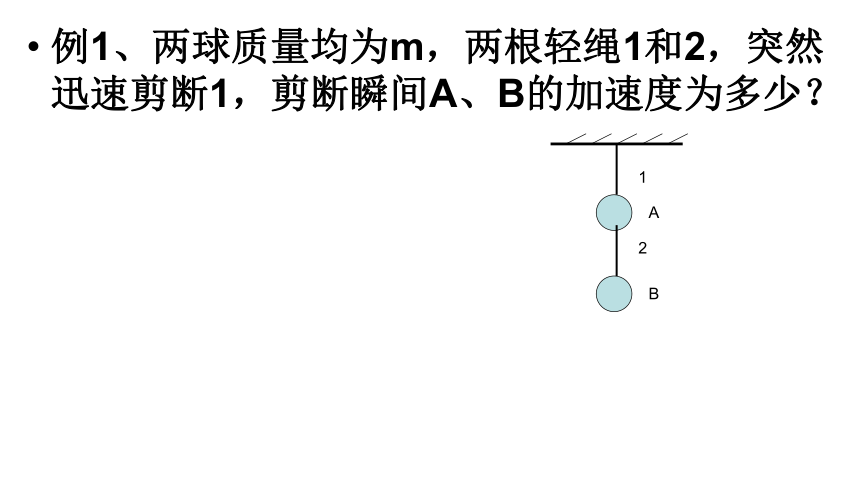
例1、两球质量均为m,两根轻绳1和2,突然迅速剪断1,剪断瞬间A、B的加速度为多少?
1
A
2
B
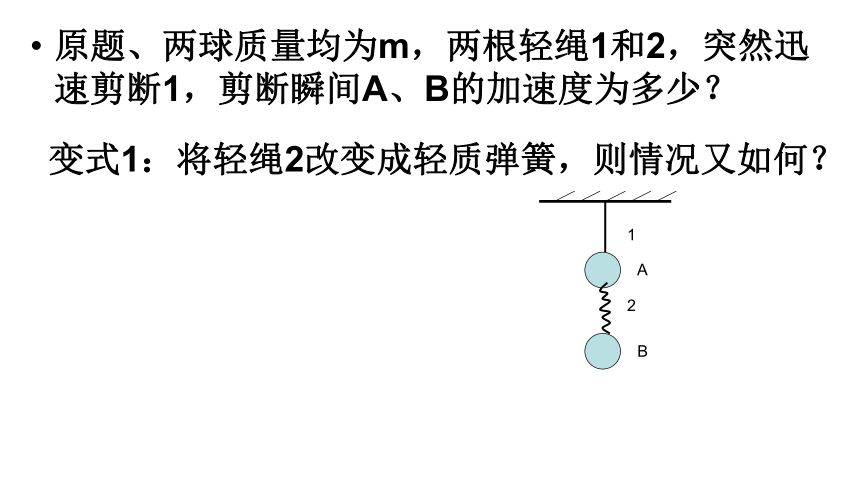
原题、两球质量均为m,两根轻绳1和2,突然迅速剪断1,剪断瞬间A、B的加速度为多少?
变式1:将轻绳2改变成轻质弹簧,则情况又如何?
1
A
2
B
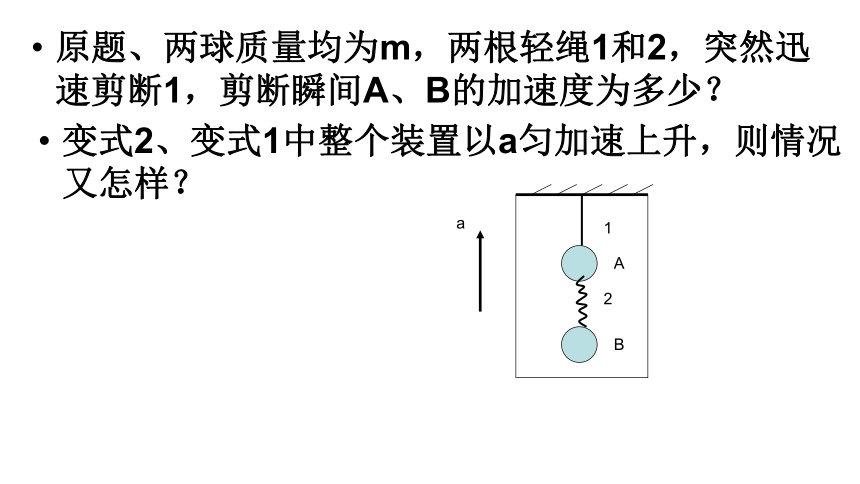
原题、两球质量均为m,两根轻绳1和2,突然迅速剪断1,剪断瞬间A、B的加速度为多少?
变式2、变式1中整个装置以a匀加速上升,则情况又怎样?
1
A
2
B
a
变式3、质量为mA、mB的两物体在粗糙的水平面上,在水平外力F的作用下匀速运动,求撤去外力F时A、B两物体的加速度为多少?
F
B
A
变式4、光滑的水平面上有一小车,以向右的加速度a匀加速运动,车内两物体A、B质量均为m,A、B间弹簧相连,通过绳子B与车相连,剪断绳子的瞬间,A、B的加速度分别为多少?
B
A
a
例2、如图(a)所示,一质量为m的物体系于长度分别为L1、L2的两根细绳上,L1的一端悬挂在天花板上,与竖直方向夹角为θ,L2水平拉直,物体处于平衡状态,现将L2线剪断,求剪断瞬间物体的加速度。
(2)若将图a中的细线L1改为长度相同、质量不计的轻弹簧,如图b所示,其他条件不变,现将L2线剪断,求剪断瞬间物体的加速度。
a=gsinθ
a=gtanθ
例3、如图,质量相同的物块A、B、C用两个轻弹簧和一根轻线相连,挂在天花板上处于平衡状态。现将A、B之间的轻绳剪断,在刚剪断的瞬间,三个物块的加速度分别是多大?方向如何?
A
B
C
例4、如图3-2-8所示是两根轻弹簧与两个质量都为m的小球连接成的系统,上面一根弹簧的上端固定在天花板上,两小球之间还连接了一根不可伸长的细线.该系统静止,细线受到的拉力大小等于4mg.在剪断了两球之间的细线的瞬间,球A的加速度aA和球B的加速度aB分别是 ( )
A.2g,竖直向下;2g,竖直向下
B.4g,竖直向上;4g,竖直向下
C.2g,竖直向上;2g,竖直向下
D.2g,竖直向下;4g,竖直向下
B
练习1、如图所示,竖直光滑杆上套有一个小球和两个弹簧,两弹簧的一端各与小球相连,另一端用销钉M、N固定于杆上,小球处于静止状态,设拨去销钉M瞬间,小球加速度a的大小为12m/s2,若不拨去销钉M而拨去销钉N瞬间,小球的加速度可能是:
A.22m/s2,竖直向上
B.22m/s2,竖直向下
C.2m/s2,竖直向上
D.2m/s2,竖直向下
M
N
( BC)
练习2、如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为1200,小球平衡时, A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为
①g/2,竖直向下;②g/2,竖直向上;
③g/4,竖直向下;④g/4,竖直向上;
A、①②;B、①④;C、②③;D、③④;
B
C
A
m
答案C.
练习3、如图3-2-10所示,A、B两物体中间用一轻质弹簧相连,静止在外框C的底板上,整个装置用一根细绳吊在天花板上,处于静止状态.A、B、C质量都为M,现在将细绳剪断,剪断后瞬间A、B、C的加速度分别为 ( )
A.g g g
B.0 g g
C.0 3g/2 3g/2
D.0 0 3g
牛顿运动定律运用之
瞬时性问题专题
一、瞬时性问题
(1)物体运动的加速度a与其所受的合外力F有瞬时对应关系,所谓瞬时性,就是物体的加速度与其所受的合外力有瞬时对应的关系,每一瞬时的加速度只取决于这一瞬时的合外力。也就是物体一旦受到不为零的合外力的作用,物体立即产生加速度;当合外力的方向、大小改变时,物体的加速度方向、大小也立即发生相应的改变;当物体的合外力为零时,物体的加速度也立即为零。由此可知,力和加速度之间是瞬时对应的。(物体运动的加速度可以突变)。
二、突变类问题(力的瞬时性)
(2)A. 刚性绳(或接触面)一旦不发生明显形变就能产生弹力的物体,剪断(或脱离)后,弹力立即消失或改变,不需要形变恢复时间,在瞬时问题中,其弹力可以突变,成为零或者别的值。一般题目中所给的细线、轻杆和接触面在不加特殊说明时,均可按此模型处理。
(3)B. 轻弹簧(或橡皮绳)发生明显形变,需要较长的形变恢复时间,在瞬时问题中其弹力不能突变,大小方向均不变。
二、突变类问题(力的瞬时性)
例1、两球质量均为m,两根轻绳1和2,突然迅速剪断1,剪断瞬间A、B的加速度为多少?
1
A
2
B
原题、两球质量均为m,两根轻绳1和2,突然迅速剪断1,剪断瞬间A、B的加速度为多少?
变式1:将轻绳2改变成轻质弹簧,则情况又如何?
1
A
2
B
原题、两球质量均为m,两根轻绳1和2,突然迅速剪断1,剪断瞬间A、B的加速度为多少?
变式2、变式1中整个装置以a匀加速上升,则情况又怎样?
1
A
2
B
a
变式3、质量为mA、mB的两物体在粗糙的水平面上,在水平外力F的作用下匀速运动,求撤去外力F时A、B两物体的加速度为多少?
F
B
A
变式4、光滑的水平面上有一小车,以向右的加速度a匀加速运动,车内两物体A、B质量均为m,A、B间弹簧相连,通过绳子B与车相连,剪断绳子的瞬间,A、B的加速度分别为多少?
B
A
a
例2、如图(a)所示,一质量为m的物体系于长度分别为L1、L2的两根细绳上,L1的一端悬挂在天花板上,与竖直方向夹角为θ,L2水平拉直,物体处于平衡状态,现将L2线剪断,求剪断瞬间物体的加速度。
(2)若将图a中的细线L1改为长度相同、质量不计的轻弹簧,如图b所示,其他条件不变,现将L2线剪断,求剪断瞬间物体的加速度。
a=gsinθ
a=gtanθ
例3、如图,质量相同的物块A、B、C用两个轻弹簧和一根轻线相连,挂在天花板上处于平衡状态。现将A、B之间的轻绳剪断,在刚剪断的瞬间,三个物块的加速度分别是多大?方向如何?
A
B
C
例4、如图3-2-8所示是两根轻弹簧与两个质量都为m的小球连接成的系统,上面一根弹簧的上端固定在天花板上,两小球之间还连接了一根不可伸长的细线.该系统静止,细线受到的拉力大小等于4mg.在剪断了两球之间的细线的瞬间,球A的加速度aA和球B的加速度aB分别是 ( )
A.2g,竖直向下;2g,竖直向下
B.4g,竖直向上;4g,竖直向下
C.2g,竖直向上;2g,竖直向下
D.2g,竖直向下;4g,竖直向下
B
练习1、如图所示,竖直光滑杆上套有一个小球和两个弹簧,两弹簧的一端各与小球相连,另一端用销钉M、N固定于杆上,小球处于静止状态,设拨去销钉M瞬间,小球加速度a的大小为12m/s2,若不拨去销钉M而拨去销钉N瞬间,小球的加速度可能是:
A.22m/s2,竖直向上
B.22m/s2,竖直向下
C.2m/s2,竖直向上
D.2m/s2,竖直向下
M
N
( BC)
练习2、如图所示,小球质量为m,被三根质量不计的弹簧A、B、C拉住,弹簧间的夹角均为1200,小球平衡时, A、B、C的弹力大小之比为3:3:1,当剪断C瞬间,小球的加速度大小及方向可能为
①g/2,竖直向下;②g/2,竖直向上;
③g/4,竖直向下;④g/4,竖直向上;
A、①②;B、①④;C、②③;D、③④;
B
C
A
m
答案C.
练习3、如图3-2-10所示,A、B两物体中间用一轻质弹簧相连,静止在外框C的底板上,整个装置用一根细绳吊在天花板上,处于静止状态.A、B、C质量都为M,现在将细绳剪断,剪断后瞬间A、B、C的加速度分别为 ( )
A.g g g
B.0 g g
C.0 3g/2 3g/2
D.0 0 3g
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
