苏教版高一数学必修四平面向量与三角恒等变换2019年秋期末复习(word)
文档属性
| 名称 | 苏教版高一数学必修四平面向量与三角恒等变换2019年秋期末复习(word) |  | |
| 格式 | zip | ||
| 文件大小 | 579.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 21:59:53 | ||
图片预览




文档简介
高一数学期末必修四重点内容复习
年级 高一 科目 数学 上课时间
课题 三角恒等变换与平面向量
四、三角函数的图像与性质
根据题意确定三角函数的参数值
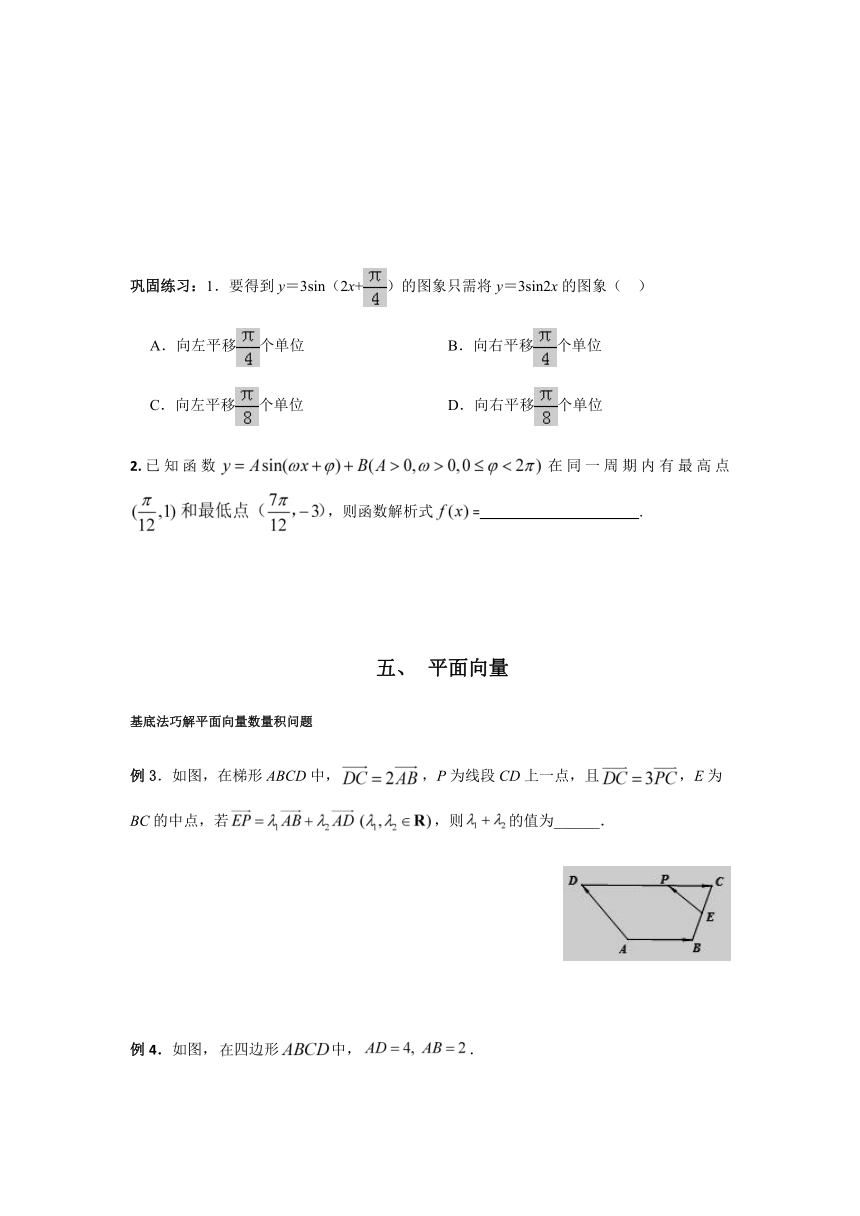
例1.如图是函数(,,)
在一个周期内的图象,则其解析式是 .
A. B.
C. D.
三角函数图像的平移与伸缩变换:左加右减,上加下减
例2.已知向量,,设.
(1)将的图像向右平移个单位,然后纵坐标不变,横坐标变为原来的2倍得到的图像,求的单调增区间;
(2)若时,恒成立,求实数的取值范围.
巩固练习:1.要得到y=3sin(2x+)的图象只需将y=3sin2x的图象( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
2.已知函数在同一周期内有最高点,则函数解析式= .
5、 平面向量
基底法巧解平面向量数量积问题
例3.如图,在梯形ABCD中,,P为线段CD上一点,且,E为BC的中点,若,则的值为______.
例4.如图,四边形中,.
(1)若△为等边三角形,且,是的中点,求;
(2)若,,,求.
巩固练习:1.若等边三角形ABC的边长为2,边BC上一点D满足,则 .
2.在△ABC中,已知AB=AC,BC=2,点P在边BC上,若,则 .
3.已知AD,BE为△ABC的中线,AD=3,BE=2,且与的夹角的余弦值为﹣,则= .
小贴士:1.在平行四边形中一般选取邻边作为基底;
2.在一般几何图形中,尽量选取已知夹角或已知长度、数量积的边长作为基底;
3.在等腰三角形等对称图形中往往选取轴对称与底边上线段作为基底。
平面向量数量积的应用
例5.已知向量满足,则= .
A. B. C. D.
例6.已知向量=(1,﹣2),=(sin(θ﹣),cos()).若⊥,则tanθ= .
巩固练习:1.设向量=(4,2),=(1,﹣1),若,则实数的值是 .
2.已知,,且与的夹角为钝角,则实数的取值范围是 .
6、 三角恒等变换
拆角与变角问题(角范围的确定)
例7.若,则 .
例8.若均为锐角,,则 .
三角恒等变换与平面向量的大题综合
例9.已知,,函数.
(1)求在区间上的最大值和最小值;
(2)若,,求的值;
(3)若函数在区间上是单调递增函数,求正数的取值范围.
巩固练习:1.在平面直角坐标系中,点在单位圆上,且点在第一象限,横坐标是,将点绕原点顺时针旋转到点,则点的横坐标为 .
A. B. C. D.
2.已知,,且,,则的值为 .
3.当取得最大值时, .
4.已知函数,将的图象上所有点横坐标扩大到原来的2倍(纵坐标不变)得到的图象.
(1)试求的单调减区间;
(2)若,求的值.
出门测(2)
1.已知角α的终边经过点P(﹣x,﹣6),且cosα=﹣,则实数x的值为( )
A.5 B. C. D.﹣5
2.已知向量,,则向量与的夹角为 .
A. B. C.或 D.
3.三角形中,已知,,,
,,则= .
4.已知,函数,.
(1) 当时,求函数在上的最大值和最小值;
(2) 若在区间上不单调,求的取值范围.
5.在三角形中,,,,是线段上一点,且,
为线段上一点.
(1)设,,设,求;.
(2)求的取值范围;
(3)若为线段的中点,直线与相交于点,求.
课后作业(2)
1. 已知弧长为的弧所对的圆心角为,则这条弧所在的扇形面积为 .
A. B. C. D.
2. 若,则 .
A. B. C. D.
3.若,则 .
4.已知f(x)=2sin(ωx+)(其中ω>0)的单调递增区间为[﹣,](k∈Z),则θ= .
5.如图,在中,,是边上一点,,则的值为 .
6.在平面直角坐标系中,O为坐标原点,A、B、C三点满足.
(Ⅰ)求证:A、B、C三点共线; (Ⅱ)求的值;
(Ⅲ)已知A(1,cosx)、B(1+cosx,cosx),x∈,f (x)= 的最小 值为,求实数m的值.
参 考 答 案
例1.B 例2.(1);(2)
巩固练习:1.C 2.
例3. 例4.(1)11;(2) 巩固练习:1. 2. 3.
例5.C 例6. 巩固练习:1.-10 2.
例7. 例8. 例9.(1);(2);(3)
巩固练习:1.B 2. 3. 4.(1);(2)
出门测(2):1.B 2.A 3. 4.(1);
(2) 5.(1);(2);(3)
课后作业(2):1.C 2.D 3. 4. 5.
6.(1)证明(略);(2)2;(3)
