北师大版数学八年级下册:6.4多边形的内角和与外角和 课件(共34张PPT)
文档属性
| 名称 | 北师大版数学八年级下册:6.4多边形的内角和与外角和 课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 8.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-26 20:48:34 | ||
图片预览




文档简介
(共34张PPT)
6.4 多边形的内角和与外角和(1)
多边形的内角和
定向示标
1.了解多边形的概念,经历探究多边形内角和公式的过程,进一步发展合情推理能力
2.会用多边形内角和公式解决相应的实际问题
重点:探究多边形内角和公式
难点:综合运用多边形内角和公式
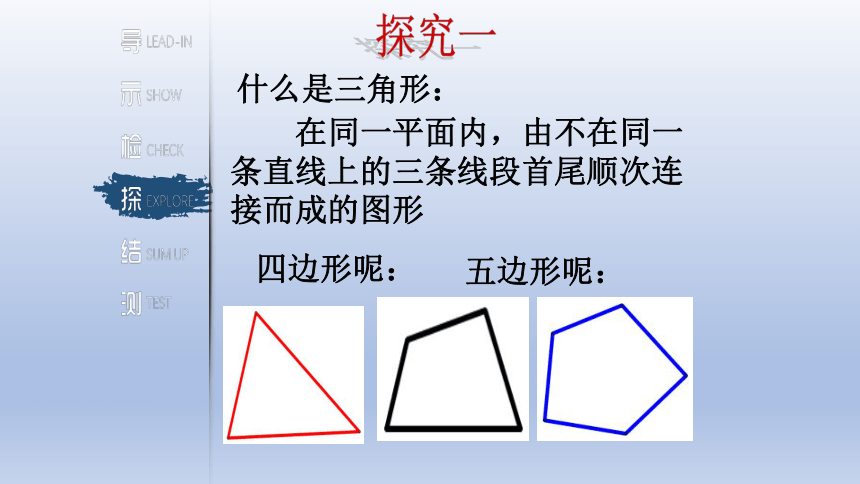
在同一平面内,由不在同一条直线上的三条线段首尾顺次连接而成的图形
什么是三角形:
四边形呢:
五边形呢:
探究一
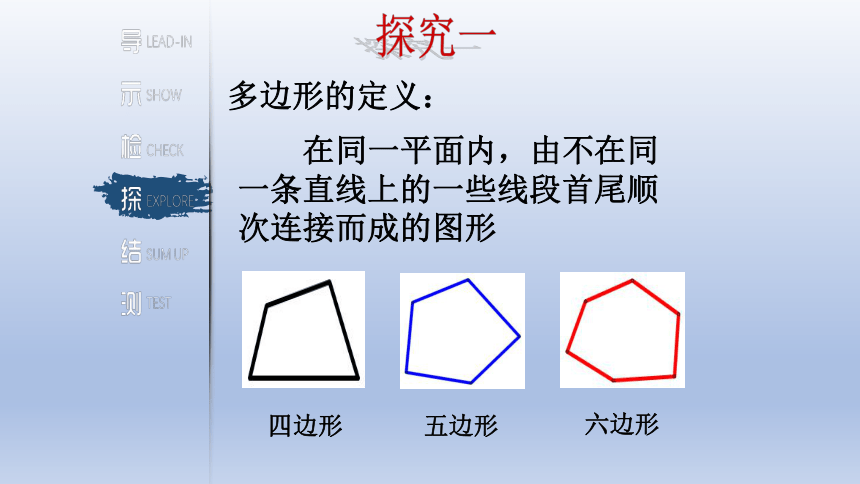
多边形的定义:
在同一平面内,由不在同一条直线上的一些线段首尾顺次连接而成的图形
探究一
四边形
五边形
六边形
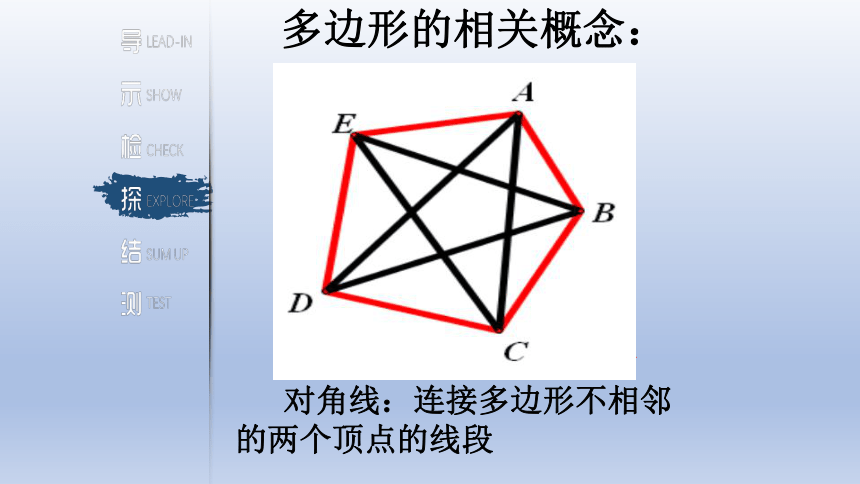
多边形的相关概念:
对角线:连接多边形不相邻的两个顶点的线段
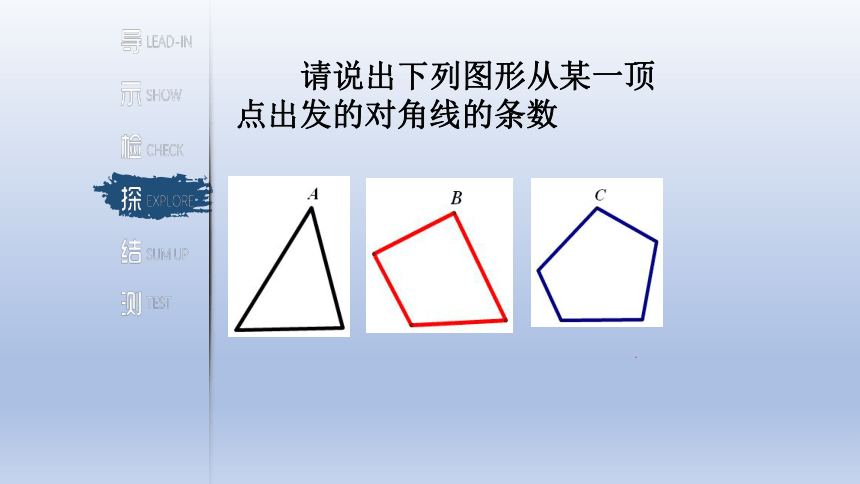
请说出下列图形从某一顶点出发的对角线的条数
(1)三角形的内角和等于___
(2)长方形的内角和等于___
(3) 正方形的内角和等于___
180°
360°
360°
想一想:
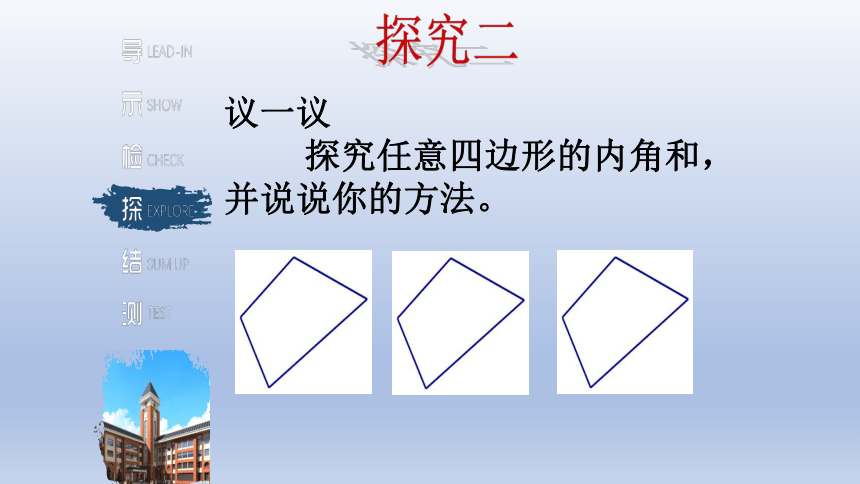
议一议
探究任意四边形的内角和,并说说你的方法。
探究二
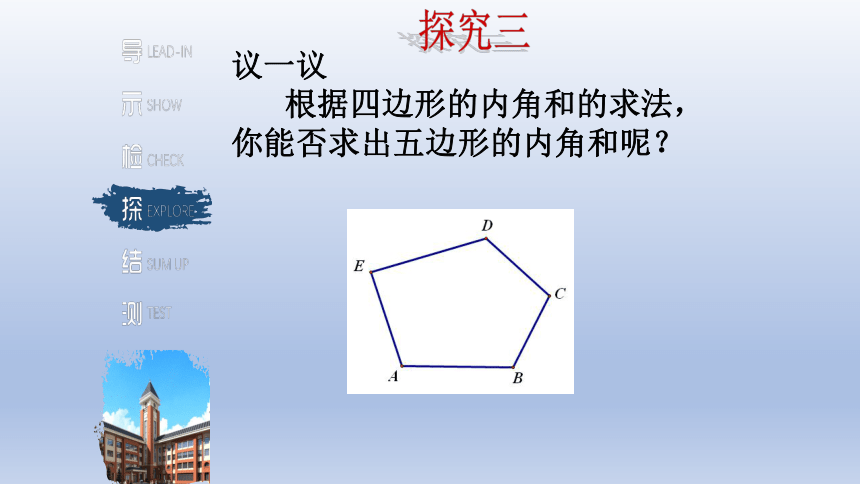
议一议
根据四边形的内角和的求法,你能否求出五边形的内角和呢?
探究三
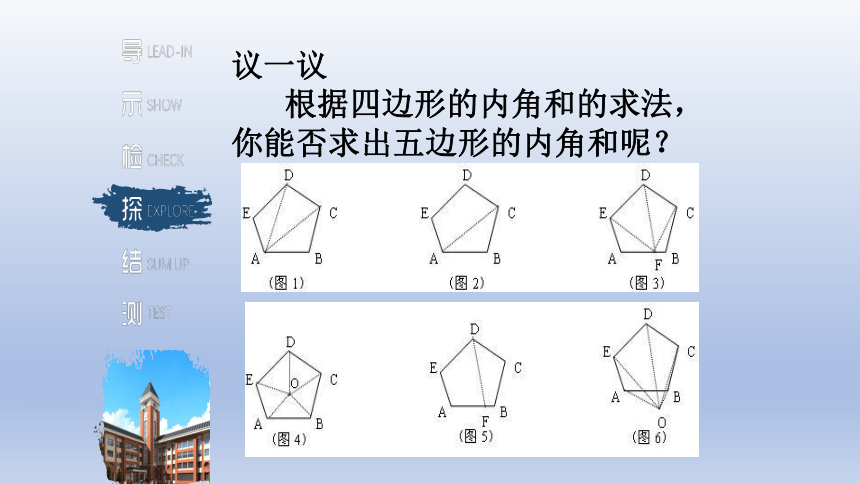
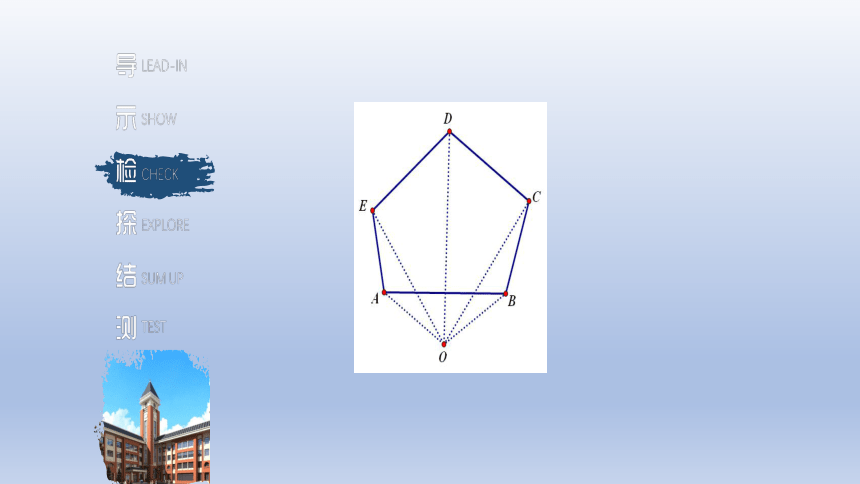
议一议
根据四边形的内角和的求法,你能否求出五边形的内角和呢?
完成下面的表格
0
1
180°
1
2
2 × 180°
2
3
3 × 180°
3
4
4 × 180°
(n-3)
(n-2)
(n-2) × 180°
n边形的内角和等于 (n-2) 180°
多边形内角和定理
例1、一个多边形的内角和为1080°,它是几边形?
生活中的多边形
如果多边形各边都相等,各个角也都相等,那么这样的多边形叫做正多边形.
正三边形
正四边形
正五边形
正六边形
正多边形:
你能求出下列正多边形的每个内角吗
图形 正多边形 内角和 每个内角
正三角形
正四边形
正五边形
正六边形
正n边形
…
想一想
180°
(n-2)180°
360°
540°
720°
90°
60°
120°
108°
(n-2)180°
n
例2、一个多边形的每个内角都等于120°,则这个多边形的边数为多少?
1、在四边形的四个内角中,最多有几个钝角?最多能有几个锐角?
2、过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?
基础训练
240°
3、如图,有一个角60°的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2 =
100°
4、如图,四边形ABCD中, ∠A+∠B=200 °, ∠ADC、 ∠DCB的平分线相交于点O,则∠COD的度数
5、工人师傅将一个长方形的桌面用锯子锯掉一个角,还剩几个角?剩下残余桌面所有的内角和是多少?
6、一个多边形剪去一个角后,形成另一个多边形的内角和为2520°则原多边形的边数为
提高题
7、小彬求出一个正多边形的一个内角为145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
提高题
8、如图所示,分别在三角形、四边形的广场各角修建半径为R m的扇形草坪(阴影部分).
(1)图1中的草坪的面积为 _____
(2)图2中的草坪的面积为 _____
0.5兀R2 ㎡
兀R2 ㎡
拓展提高
,
谈谈你本节课的收获
课堂小结
布置作业
1、《课本》第155页1、2、3
2、《课堂精炼》第169页、170页
最后,老师真心地希望大家:
也许我跑的并不是最快的,但我却是最坚持的一个;
也许我跳得并不是最远的,但我是最用力起跳的那一个;
也许我思维并不是最敏捷的,但我是最认真思考的一个;
我相信,同学们只要有学好数学的信心,决心
和恒心。一定会将数学学得多姿多彩。
寄语
6.4 多边形的内角和与外角和(1)
多边形的内角和
定向示标
1.了解多边形的概念,经历探究多边形内角和公式的过程,进一步发展合情推理能力
2.会用多边形内角和公式解决相应的实际问题
重点:探究多边形内角和公式
难点:综合运用多边形内角和公式
在同一平面内,由不在同一条直线上的三条线段首尾顺次连接而成的图形
什么是三角形:
四边形呢:
五边形呢:
探究一
多边形的定义:
在同一平面内,由不在同一条直线上的一些线段首尾顺次连接而成的图形
探究一
四边形
五边形
六边形
多边形的相关概念:
对角线:连接多边形不相邻的两个顶点的线段
请说出下列图形从某一顶点出发的对角线的条数
(1)三角形的内角和等于___
(2)长方形的内角和等于___
(3) 正方形的内角和等于___
180°
360°
360°
想一想:
议一议
探究任意四边形的内角和,并说说你的方法。
探究二
议一议
根据四边形的内角和的求法,你能否求出五边形的内角和呢?
探究三
议一议
根据四边形的内角和的求法,你能否求出五边形的内角和呢?
完成下面的表格
0
1
180°
1
2
2 × 180°
2
3
3 × 180°
3
4
4 × 180°
(n-3)
(n-2)
(n-2) × 180°
n边形的内角和等于 (n-2) 180°
多边形内角和定理
例1、一个多边形的内角和为1080°,它是几边形?
生活中的多边形
如果多边形各边都相等,各个角也都相等,那么这样的多边形叫做正多边形.
正三边形
正四边形
正五边形
正六边形
正多边形:
你能求出下列正多边形的每个内角吗
图形 正多边形 内角和 每个内角
正三角形
正四边形
正五边形
正六边形
正n边形
…
想一想
180°
(n-2)180°
360°
540°
720°
90°
60°
120°
108°
(n-2)180°
n
例2、一个多边形的每个内角都等于120°,则这个多边形的边数为多少?
1、在四边形的四个内角中,最多有几个钝角?最多能有几个锐角?
2、过某个多边形一个顶点的所有对角线,将这个多边形分成5个三角形,这个多边形是几边形?它的内角和是多少?
基础训练
240°
3、如图,有一个角60°的三角形纸片,剪去这个60°角后,得到一个四边形,则∠1+∠2 =
100°
4、如图,四边形ABCD中, ∠A+∠B=200 °, ∠ADC、 ∠DCB的平分线相交于点O,则∠COD的度数
5、工人师傅将一个长方形的桌面用锯子锯掉一个角,还剩几个角?剩下残余桌面所有的内角和是多少?
6、一个多边形剪去一个角后,形成另一个多边形的内角和为2520°则原多边形的边数为
提高题
7、小彬求出一个正多边形的一个内角为145°,他的计算正确吗?如果正确,他求的是正几边形的内角?如果不正确,请说明理由.
提高题
8、如图所示,分别在三角形、四边形的广场各角修建半径为R m的扇形草坪(阴影部分).
(1)图1中的草坪的面积为 _____
(2)图2中的草坪的面积为 _____
0.5兀R2 ㎡
兀R2 ㎡
拓展提高
,
谈谈你本节课的收获
课堂小结
布置作业
1、《课本》第155页1、2、3
2、《课堂精炼》第169页、170页
最后,老师真心地希望大家:
也许我跑的并不是最快的,但我却是最坚持的一个;
也许我跳得并不是最远的,但我是最用力起跳的那一个;
也许我思维并不是最敏捷的,但我是最认真思考的一个;
我相信,同学们只要有学好数学的信心,决心
和恒心。一定会将数学学得多姿多彩。
寄语
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
