24.1.1 旋转(基础达标+巩固提升+答案)
文档属性
| 名称 | 24.1.1 旋转(基础达标+巩固提升+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 00:00:00 | ||
图片预览

文档简介
沪科版数学九年级下册同步课时训练
第24章 圆
24.1 旋 转
第1课时 旋 转
要点测评 基础达标
要点1 旋转
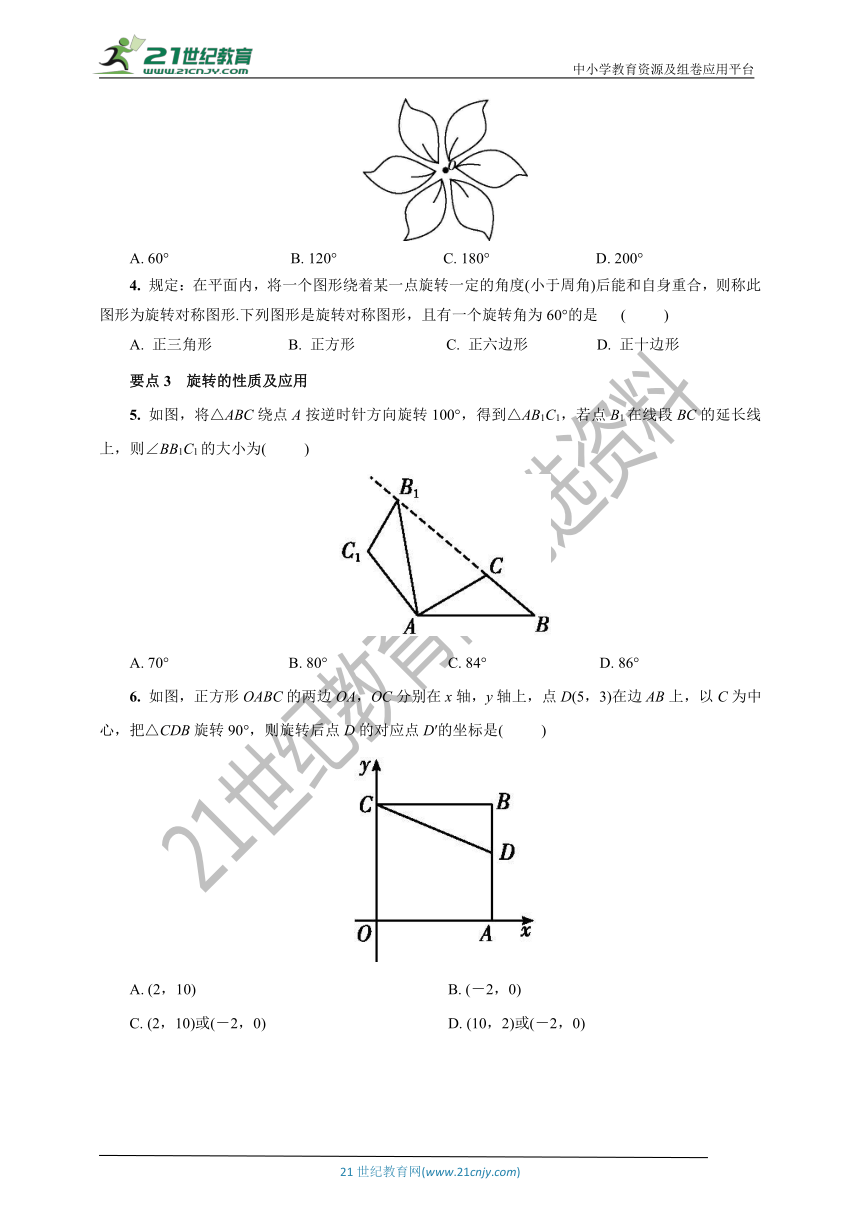
1. 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A. 60° B. 90° C. 120° D. 150°
2. 如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置.
(1)请指出旋转中心;
(2)旋转了多少度;
(3)指出线段AE的对应线段;
(4)指出∠B和∠BAD的对应角;
(5)若点F是线段AD的中点,则经过上述旋转后,点F旋转到了什么位置?请在图中画出来.
要点2 旋转对称图形
3. 如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A. 60° B. 120° C. 180° D. 200°
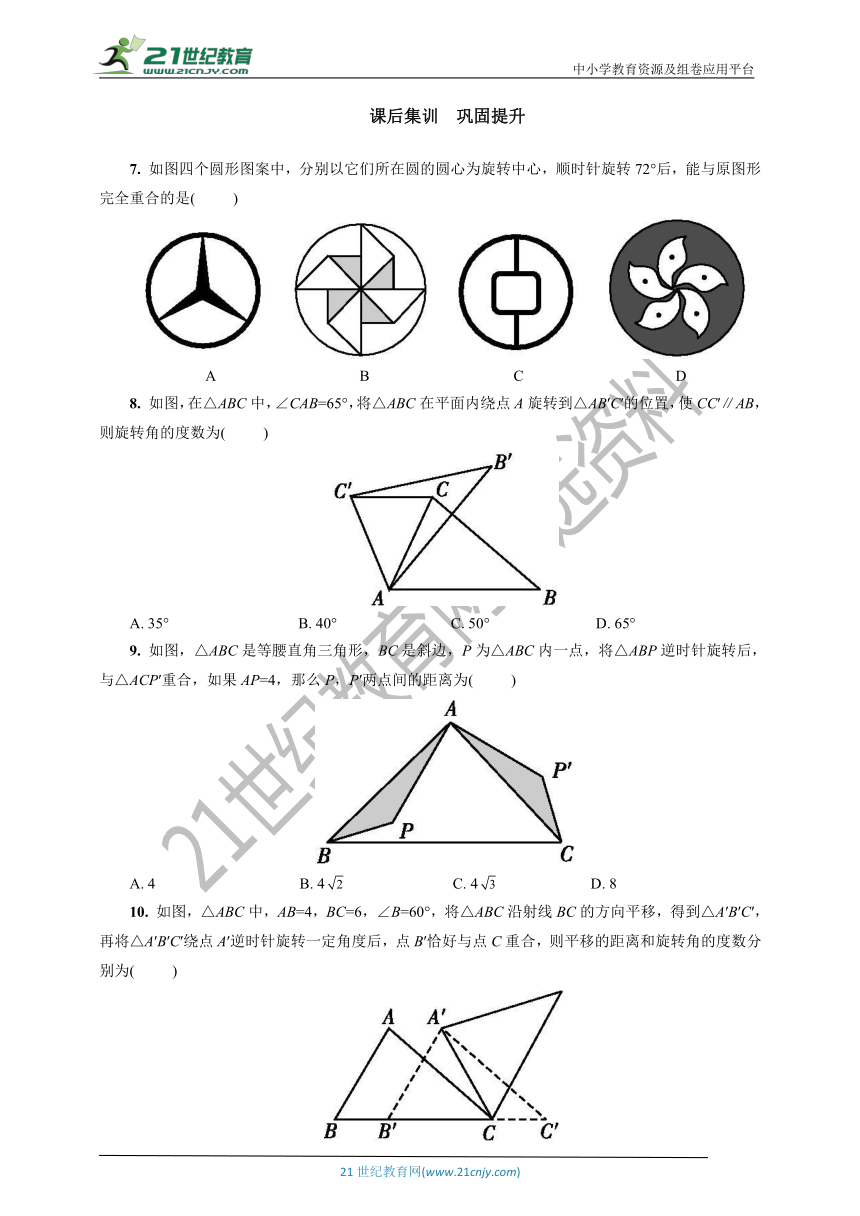
4. 规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,则称此图形为旋转对称图形.下列图形是旋转对称图形,且有一个旋转角为60°的是 ( )
A. 正三角形 B. 正方形 C. 正六边形 D. 正十边形
要点3 旋转的性质及应用
5. 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
A. 70° B. 80° C. 84° D. 86°
6. 如图,正方形OABC的两边OA,OC分别在x轴,y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A. (2,10) B. (-2,0)
C. (2,10)或(-2,0) D. (10,2)或(-2,0)
课后集训 巩固提升
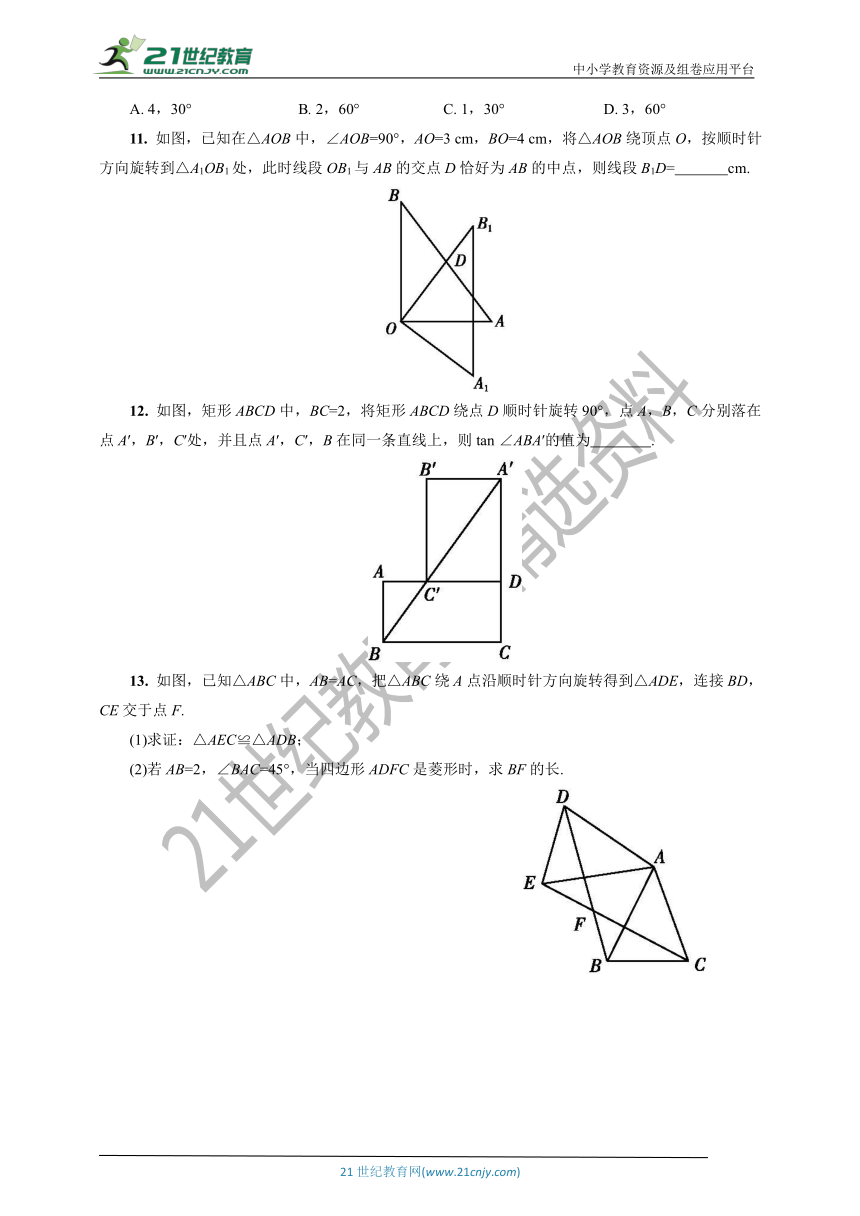
7. 如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转72°后,能与原图形完全重合的是( )
A B C D
8. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A. 35° B. 40° C. 50° D. 65°
9. 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
A. 4 B. 4 C. 4 D. 8
10. 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )
A. 4,30° B. 2,60° C. 1,30° D. 3,60°
11. 如图,已知在△AOB中,∠AOB=90°,AO=3 cm,BO=4 cm,将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D= cm.
12. 如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,B,C分别落在点A′,B′,C′处,并且点A′,C′,B在同一条直线上,则tan ∠ABA′的值为 .
13. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
14. 如图,已知△ABC中,∠C=90°,AC=BC=2,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,求C′B的长.
参 考 答 案
1. D 【解析】旋转角是∠CAC′=180°-30°=150°,故选D.
2. 解:(1)图形在旋转过程中“不动”的点就是旋转中心即点A是旋转中心.
(2)点B与点C是对应点,∠BAC=60°,所以旋转了60°.
(3)点D与点E是对应点,所以线段AE的对应线段是AD.
(4)点B与点C是对应点,点D与点E是对应点,所以∠B的对应角是∠ACE,∠BAD的对应角是∠CAE.
(5)AD与AE是对应线段,点F是线段AD的中点,所以点F的对应点是线段AE的中点M(如图).
3. D 【解析】360°÷6=60°,故该图形只需旋转60°的整数倍都能与自身重合.
4. C 【解析】正三角形的最小旋转角是120°,故A错误;正方形的旋转角度是90°,故B错误;正六边形的最小旋转角是60°,故C正确;正十边形的最小旋转角是36°,故D错误;故选C.
5. B 【解析】由旋转的性质可知∠B=∠AB1C1,AB=AB1;∠BAB1=100°,所以∠B=∠BB1A=40°,所以∠AB1C1=40°,所以∠BB1C1=∠BB1A+∠AB1C1=40°+40°=80°.故选B.
6. C 【解析】因为点D(5,3)在边AB上,所以BC=5,BD=5-3=2,①若顺时针旋转,则点D′在x轴上,OD′=2,所以D′(-2,0),②若逆时针旋转,则点D′到x轴的距离为10,到y轴的距离为2,所以D′(2,10),综上所述,点D′的坐标为(2,10)或(-2,0),故选C.
7. D 【解析】选项A图形顺时针旋转120°后,能与原图形完全重合,故A不正确;选项B图形顺时针旋转90°后,能与原图形完全重合,故B不正确;选项C图形顺时针旋转180°后,能与原图形完全重合,故C不正确;选项D图形顺时针旋转72°后,能与原图形完全重合,故D正确.故选D.
8. C 【解析】因为CC′∥AB,所以∠ACC′=∠CAB=65°,因为△ABC绕点A旋转得到△AB′C′,所以AC=AC′,所以∠CAC′=180°-2∠ACC′=180°-2×65°=50°,所以∠CAC′=∠BAB′=50°.故选C.
9. B 【解析】如图,连接PP′,因为△ABP绕点A逆时针旋转后与△ACP′重合,所以△ABP≌△ACP′,即线段AB旋转后到AC,所以旋转了90°,所以∠PAP′=∠BAC=90°,AP=AP′=4,所以PP′===4,故选B.
10. B 【解析】因为∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,所以∠A′B′C=60°,AB=A′B′=A′C=4,所以△A′B′C是等边三角形,所以B′C=4,∠B′A′C=60°,所以BB′=6-4=2,所以平移的距离和旋转角的度数分别为2,60°.故选B.
11. 15 【解析】因为D点为AB的中点,根据“直角三角形斜边上的中线等于斜边的一半”可得OD=AB=×=2.5 cm.由题意可得OB1=OB=4 cm.所以B1D=OB1-OD=4-2.5=1.5 cm.
12. 【解析】因为四边形ABCD是矩形,所以AD=BC=2,∠A=90°,C′D∥BC,因为将矩形ABCD绕点D顺时针旋转90°,所以AB=C′D,BC=B′C′=AD=2,设AB=x,则AB=C′D=x,A′C=A′D+CD=x+2,因为C′D∥BC,所以△A′C′D∽△A′BC,所以C′D∶BC=A′D∶A′C,即x∶2=2∶(x+2),解得x=-1+或x=-1-(小于0,不合题意,舍去),所以AC′=2-C′D=2-(-1+)=3-,所以tan ∠ABA′===.
13. 解:(1)由旋转的性质得△ABC≌△ADE,且AB=AC,所以AE=AD,∠BAC=∠DAE,所以∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,在△AEC和△ADB中,所以△AEC≌△ADB(SAS).
(2)因为四边形ADFC是菱形,且∠BAC=45°,所以∠DBA=∠BAC=45°,因为AB=AD,所以∠DBA=∠ADB=45°,所以BD2=2AB2,即BD=2,又AD=DF=FC=AC=AB=2,所以BF=BD-DF=2-2.
14. 解:如图,连接BB′,延长BC′交AB′于点M;由题意得∠BAB′=60°,BA=B′A,所以△ABB′为等边三角形,所以∠ABB′=60°,AB=B′B.在△ABC′与△B′BC′中,所以△ABC′≌△B′BC′,所以∠MBB′=∠MBA=30°,所以BM⊥AB′,且AM=B′M.由题意得AB2=(2)2+(2)2=16,所以AB′=AB=4,AM=2,所以C′M=AB′=2.由勾股定理可求BM=2,所以C′B=2-2.
第24章 圆
24.1 旋 转
第1课时 旋 转
要点测评 基础达标
要点1 旋转
1. 如图所示,将一个含30°角的直角三角板ABC绕点A旋转,使得点B,A,C′在同一条直线上,则三角板ABC旋转的角度是( )
A. 60° B. 90° C. 120° D. 150°
2. 如图,△ABC是等边三角形,D是BC边上一点,△ABD经过旋转后到达△ACE的位置.
(1)请指出旋转中心;
(2)旋转了多少度;
(3)指出线段AE的对应线段;
(4)指出∠B和∠BAD的对应角;
(5)若点F是线段AD的中点,则经过上述旋转后,点F旋转到了什么位置?请在图中画出来.
要点2 旋转对称图形
3. 如图,该图形绕点O按下列角度旋转后,不能与其自身重合的是( )
A. 60° B. 120° C. 180° D. 200°
4. 规定:在平面内,将一个图形绕着某一点旋转一定的角度(小于周角)后能和自身重合,则称此图形为旋转对称图形.下列图形是旋转对称图形,且有一个旋转角为60°的是 ( )
A. 正三角形 B. 正方形 C. 正六边形 D. 正十边形
要点3 旋转的性质及应用
5. 如图,将△ABC绕点A按逆时针方向旋转100°,得到△AB1C1,若点B1在线段BC的延长线上,则∠BB1C1的大小为( )
A. 70° B. 80° C. 84° D. 86°
6. 如图,正方形OABC的两边OA,OC分别在x轴,y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A. (2,10) B. (-2,0)
C. (2,10)或(-2,0) D. (10,2)或(-2,0)
课后集训 巩固提升
7. 如图四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转72°后,能与原图形完全重合的是( )
A B C D
8. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A. 35° B. 40° C. 50° D. 65°
9. 如图,△ABC是等腰直角三角形,BC是斜边,P为△ABC内一点,将△ABP逆时针旋转后,与△ACP′重合,如果AP=4,那么P,P′两点间的距离为( )
A. 4 B. 4 C. 4 D. 8
10. 如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离和旋转角的度数分别为( )
A. 4,30° B. 2,60° C. 1,30° D. 3,60°
11. 如图,已知在△AOB中,∠AOB=90°,AO=3 cm,BO=4 cm,将△AOB绕顶点O,按顺时针方向旋转到△A1OB1处,此时线段OB1与AB的交点D恰好为AB的中点,则线段B1D= cm.
12. 如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,B,C分别落在点A′,B′,C′处,并且点A′,C′,B在同一条直线上,则tan ∠ABA′的值为 .
13. 如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
14. 如图,已知△ABC中,∠C=90°,AC=BC=2,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,求C′B的长.
参 考 答 案
1. D 【解析】旋转角是∠CAC′=180°-30°=150°,故选D.
2. 解:(1)图形在旋转过程中“不动”的点就是旋转中心即点A是旋转中心.
(2)点B与点C是对应点,∠BAC=60°,所以旋转了60°.
(3)点D与点E是对应点,所以线段AE的对应线段是AD.
(4)点B与点C是对应点,点D与点E是对应点,所以∠B的对应角是∠ACE,∠BAD的对应角是∠CAE.
(5)AD与AE是对应线段,点F是线段AD的中点,所以点F的对应点是线段AE的中点M(如图).
3. D 【解析】360°÷6=60°,故该图形只需旋转60°的整数倍都能与自身重合.
4. C 【解析】正三角形的最小旋转角是120°,故A错误;正方形的旋转角度是90°,故B错误;正六边形的最小旋转角是60°,故C正确;正十边形的最小旋转角是36°,故D错误;故选C.
5. B 【解析】由旋转的性质可知∠B=∠AB1C1,AB=AB1;∠BAB1=100°,所以∠B=∠BB1A=40°,所以∠AB1C1=40°,所以∠BB1C1=∠BB1A+∠AB1C1=40°+40°=80°.故选B.
6. C 【解析】因为点D(5,3)在边AB上,所以BC=5,BD=5-3=2,①若顺时针旋转,则点D′在x轴上,OD′=2,所以D′(-2,0),②若逆时针旋转,则点D′到x轴的距离为10,到y轴的距离为2,所以D′(2,10),综上所述,点D′的坐标为(2,10)或(-2,0),故选C.
7. D 【解析】选项A图形顺时针旋转120°后,能与原图形完全重合,故A不正确;选项B图形顺时针旋转90°后,能与原图形完全重合,故B不正确;选项C图形顺时针旋转180°后,能与原图形完全重合,故C不正确;选项D图形顺时针旋转72°后,能与原图形完全重合,故D正确.故选D.
8. C 【解析】因为CC′∥AB,所以∠ACC′=∠CAB=65°,因为△ABC绕点A旋转得到△AB′C′,所以AC=AC′,所以∠CAC′=180°-2∠ACC′=180°-2×65°=50°,所以∠CAC′=∠BAB′=50°.故选C.
9. B 【解析】如图,连接PP′,因为△ABP绕点A逆时针旋转后与△ACP′重合,所以△ABP≌△ACP′,即线段AB旋转后到AC,所以旋转了90°,所以∠PAP′=∠BAC=90°,AP=AP′=4,所以PP′===4,故选B.
10. B 【解析】因为∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,所以∠A′B′C=60°,AB=A′B′=A′C=4,所以△A′B′C是等边三角形,所以B′C=4,∠B′A′C=60°,所以BB′=6-4=2,所以平移的距离和旋转角的度数分别为2,60°.故选B.
11. 15 【解析】因为D点为AB的中点,根据“直角三角形斜边上的中线等于斜边的一半”可得OD=AB=×=2.5 cm.由题意可得OB1=OB=4 cm.所以B1D=OB1-OD=4-2.5=1.5 cm.
12. 【解析】因为四边形ABCD是矩形,所以AD=BC=2,∠A=90°,C′D∥BC,因为将矩形ABCD绕点D顺时针旋转90°,所以AB=C′D,BC=B′C′=AD=2,设AB=x,则AB=C′D=x,A′C=A′D+CD=x+2,因为C′D∥BC,所以△A′C′D∽△A′BC,所以C′D∶BC=A′D∶A′C,即x∶2=2∶(x+2),解得x=-1+或x=-1-(小于0,不合题意,舍去),所以AC′=2-C′D=2-(-1+)=3-,所以tan ∠ABA′===.
13. 解:(1)由旋转的性质得△ABC≌△ADE,且AB=AC,所以AE=AD,∠BAC=∠DAE,所以∠BAC+∠BAE=∠DAE+∠BAE,即∠CAE=∠DAB,在△AEC和△ADB中,所以△AEC≌△ADB(SAS).
(2)因为四边形ADFC是菱形,且∠BAC=45°,所以∠DBA=∠BAC=45°,因为AB=AD,所以∠DBA=∠ADB=45°,所以BD2=2AB2,即BD=2,又AD=DF=FC=AC=AB=2,所以BF=BD-DF=2-2.
14. 解:如图,连接BB′,延长BC′交AB′于点M;由题意得∠BAB′=60°,BA=B′A,所以△ABB′为等边三角形,所以∠ABB′=60°,AB=B′B.在△ABC′与△B′BC′中,所以△ABC′≌△B′BC′,所以∠MBB′=∠MBA=30°,所以BM⊥AB′,且AM=B′M.由题意得AB2=(2)2+(2)2=16,所以AB′=AB=4,AM=2,所以C′M=AB′=2.由勾股定理可求BM=2,所以C′B=2-2.
