4.6 用牛顿运动定律解决问题(一)(共52张PPT)
文档属性
| 名称 | 4.6 用牛顿运动定律解决问题(一)(共52张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 669.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2019-12-27 00:00:00 | ||
图片预览










文档简介
(共53张PPT)
4.6 用牛顿运动定律解决问题(一)
一、牛顿第二定律
内容: 物体的加速度与所受的合力成正比,跟物体的质量成反比,加速度的方向跟合力的方向相同。
教学复习:
数学表达式: F=ma
4.独立性
1.同体性
2.矢量性
3.瞬时性
四性:
速度公式 : vt = vo+at
位移公式: x= vot +0.5at2
导出公式: x=(vt 2- vo 2)/2a
二、运动学知识
教学复习:
动力学的两类基本问题:
1、已知物体的受力情况求物体的运动情况。
2、已知物体的运动情况求物体的受力情况。
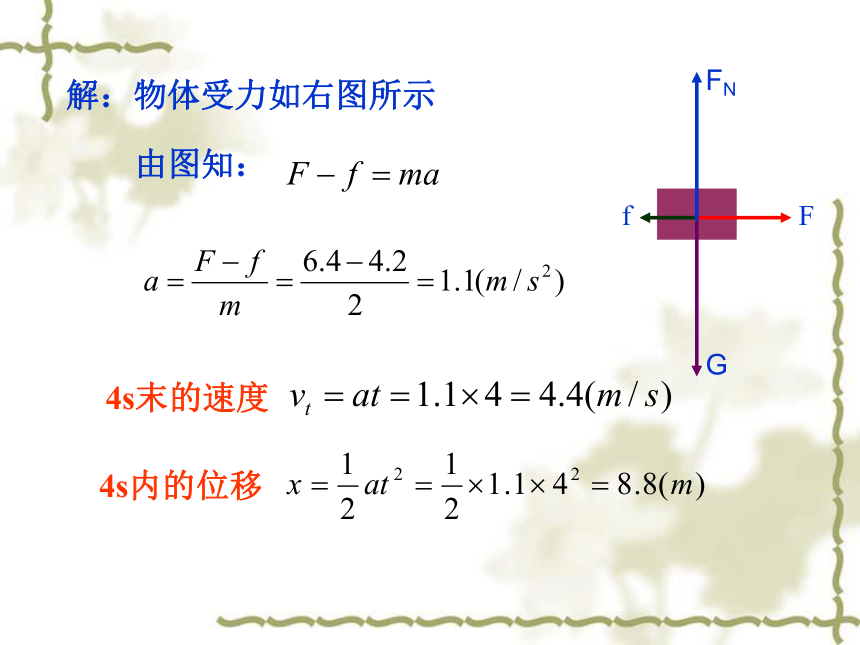
例题 1:一个静止在水平地面上的物体,质量是 2kg,在 6.4N的水平拉力作用下沿水平地面向右运动。物体与地面间的摩擦力是4.2N。求物体在4s末的速度和4s内的位移。
问:l、本题研究对象是谁?它共受几个力的作用?物体所受的合力沿什么方向?大小是多少?
2、本题要求计算位移和速度,而我们只会解决匀变速运动问题。这个物体的运动是匀变速运动吗?依据是什么?
3、FN和G在竖直方向上,它们有什么关系?
一、从受力确定运动情况
解:物体受力如右图所示
4s末的速度
4s内的位移
由图知:
说明:解题中求合力的计算式往往和牛二定律结合在一起,而运动学公式单独列出。
解:物体受力如右图所示
4s末的速度
4s内的位移
由图知:
3.利用运动学公式确定物体的运动情况.
解题步骤:
1.确定研究对象,并对物体进行受力分析,弄清题目的物理情景。
2.求出合力,利用牛顿第二定律求出物体的加速度。
例题 2:一个滑雪的人质量是 75 kg,以v0=2m/s的初速度沿山坡匀加速滑下,山坡的倾角θ=30°。在 t=5s的时间内滑下的路程x=60m,求滑雪人受到的阻力(包括摩擦和空气阻力)。
问:1、本题属于那类力学问题?
2、人共受几个力的作用?各力方向如何?
3、它们之中哪个力是已知的?哪个力实际上是己知的?待求力是谁?
4、物体所受的合力沿什么方向?
二、从运动情况确定受力
思路:应先求出加速度a,再利用牛顿第二定律F合=ma求滑雪人受到的阻力。
解:对人进行受力分析,建立坐标系,
把重力进行正交分解得:
Gx=mgsinθ
Gy=mgcosθ
由x=v0t+ at2 得:
代入已知量的数值得:a=4m/s2
根据牛顿第二定律有Gx-F阻=ma
F阻=Gx-ma=mgsinθ-ma
代入数值得:F阻=67.5N
即:滑雪人受到的阻力是67.5N。
2.根据物体的运动情况对物体运用运动学公式求出加速度。
解题步骤:
4.结合物体受力分析求出所求的力。
3.根据牛顿第二定律求出合力。
1.对物体进行受力分析并建立题目中的物理情景.
1.已知物体的受力情况求物体的运动情况。
总结:
据
求a
由受力情况求合力
F=ma
求得x,vt,vo等
一、两类问题:
2.已知物体的运动情况求物体的受力情况。
求得a
由运动情况,据
F=ma
求合力
受力分析
求受力情况
总结:
一、两类问题:
说明:两类基本问题中,受力分析是关键,牛二定律是桥梁,求解加速度是枢纽,所以不管是哪一类问题,都要设法先求出加速度。
受力情况F1、F2…
运动情况v0、s…
F合
a
力的合成与分解
牛顿第二定律
运动学公式
总结:
二、常用方法:
1.多物体问题
2.多力问题
3.多过程问题
按顺序对题目给出的物体运动过程进行分段分析的方法简称“程序法”。“程序法”要求从读题开始,就要注意题中含有多少个不同的过程或多少个不同的状态,然后对各个过程或各个状态进行分析。
——隔离法
——正交分解法
——程序法
练习:
质量为1.5Kg的物体在与水平面成37。角的拉力F为10N的力的作用下,沿着水平桌面向右做匀加速直线运动,经过一段距离,速度由5m/s变为7m/s,已知物体与桌面的摩擦力大小为5N,求物体通过的距离。
(cos 37。=0.8,sin 37。=0.6)
V0=5m/s
Vt=7m/s
已知:m=1.5kg,f=5N,g=10m/s2,F=10N,θ=37,Vt= 7m/s V0=5m/s
求: x
) θ
解:物体受到四个力的作用,如图所示。由于物体沿水平面运动,固建立如图所示的直角坐标系
x轴方向:Fcosθ-f = F合
y轴方向:Fsinθ+ F支= mg
解此方程组可得: F合 =3N
所以:a= F合 /m=2m/s2
又由公式:x=(vt2-vo2)/2a
解得:x=6m
正交分解法应用专题
所谓正交分解法是把一个矢量分解在两个互相垂直的坐标轴上的方法。
正交分解法是一种常用的矢量运算方法,也是解牛顿第二定律题目最基本的方法。物体在受到三个或三个以上的不在同一直线上的力的作用时一般都采用正交分解法。
表示方法:
建立坐标系时确定x轴的正方向一般有两种方法:
(1)分解力而不分解加速度,此时应规定加速度的方向为x轴的正方向。
(2)分解加速度而不分解力,此法一般是以某个力的方向为x轴的正方向,而其它力都落在两坐标上而不需要再分解,或者加速度已知分解方便。
1.质量为的三角形木块A置于倾角为θ的固定斜面上,它与斜面间的动摩擦因数为μ,一水平力F的推动下, 木块A沿斜面以恒定的加速度a向上滑动,如图甲所示,则力F的大小为多少?
将物体所受各力沿平行斜面方向和
垂直斜面方向正交分解,不分解加速
度,如图所示,即可得出方程组:
垂直斜面方向上有:
2.一物体放置在倾角为为θ的斜面上,斜面固定在加速上升的电梯中,加速度为a,如图所示,在物体始终相对于斜面静止的情况下,下列说法正确的是:( )
A.当θ一定时,a越大,斜面对物体的正压力越小;
B.当θ一定时,a越大,斜面对物体的摩擦力越大;
C.当a一定时,θ越大,斜面对物体的正压力越小;
D.当a一定时,θ越大,斜面对物体的摩擦力越小。
选物体为研究对象,受力如图所示,建立坐标系,注意题中物体相对于斜面静止,所以f是静摩擦力,加速度向上,所以静摩擦力f沿斜面向上。
水平方向:
当θ一定时,a变大,N、f均变大。
当a一定时,θ变大,N越小,f越大。
竖直方向:
方法1.正交分解法
方法2.合成法
当θ一定时,a变大,N、f均变大。
当a一定时,θ变大,N越小,f越大。
3.如图所示,质量为M的人站在自动扶梯上,扶梯正在以加速度a斜向上做匀减速运动,a与水平方向夹角为θ,求人受到的摩擦力和支持力?
a
物体在受到三个或三个以上的不同方向的力作用时,一般都要用到正交分解法。在建立坐标系时,不管选取哪个方向为X轴的正方向时,所得的最后结果都应是一样的。在选取坐标轴时,为使解题方便,应考虑尽量减少矢量的分解,若已知加速度方向一般以加速度方向为正方向。
“程序法” 应用专题
按顺序对题目给出的物体运动过程进行分段分析的方法简称”程序法”,“程序法”要求从读题开始,就要注意题中含有多少个不同的过程或多少个不同的状态,然后对各个过程或各个状态进行分析。
1.物体在粗糙斜面的底端O以初速V沿斜面上滑,到最高点P后又滑回到O点,那么:
A.它上滑和下滑过程中加速度的方向相同;
B.它的上滑时间比下滑时间长;
C.它在P点时速度和加速度都等于零;
D.它滑回到O点时速率一定小于v。
v
利用”逆向法”列运动学公式得:
(2)过程二:匀加速下滑,受力如图。
由牛顿第二定律得:
由运动学公式得:
(1)过程一:匀减速上滑,受力如图.
由牛顿第二定律得:
题目描述有两个过程:
1.物体在粗糙斜面的底端O以初速V沿斜面上滑,到最高点P后又滑回到O点,那么:
A.它上滑和下滑过程中加速度的方向相同;
B.它的上滑时间比下滑时间长;
C.它在P点时速度和加速度都等于零;
D.它滑回到O点时速率一定小于v。
v
比较①④式得:
比较②⑤式得:
比较③⑥式得:
B错,D对
物体在P点能滑下,
在P点合力不为零,即在P点
由分析可知,加速度均沿斜面向下
A对,C错
A、D
2、如图所示,一个弹簧台秤的秤盘的质量和弹簧的质量都不计,盘内放一个物体P处于静止,P的质量m=12kg,弹簧的劲度系数k=800N/m。现在给P施加一个竖直向上的力F,使P从静止开始向上做匀加速直线运动,已知在t=0.2s内F是变力,t=0.2s以后F是恒力,g=10m/s2,求F的最小值和最大值。
P
F
此题包括含有三个状态或过程:P静止→P压紧托盘(弹簧)向上匀加速→P离开托盘向上匀加速。
(1)过程一:弹簧被压缩x0,P静止。受力如右图甲所示,由平衡条件得:
(2)过程二:P压紧托盘(弹簧)向上匀加速,受力如右图乙所示,此一过程可用极限分析法分析:
∵向上得合力不变,∴在最低点时,向上的弹力最大,故向上的拉力必最小;物体与秤盘分离时,弹簧弹力最小(为0),故向上的拉力最大。
(3)过程三:t=0.2s后,物体离开托盘,F为恒力。
在最低点:
在最高点:
P静止在盘内时,受力如右图甲所示,
由平衡条件得:
解:
P压紧托盘(弹簧)向上匀加速,受力如右图乙所示,
②“过程二”是动态变化过程,利用“极限法”思想推向两个极端,找出最大值、最小值的条件。“程序法”和“极限法”是分析复杂过程得常用方法。
①此题要按“程序法”划分为三个阶段分析才能把整个过程得隐含条件挖掘出来。
练习、如图所示,自由下落的小球下落一段时间后与弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,小球的速度、加速度、合外力的变化情况是怎样的?
“隔离法”应用专题
在连接体中把某个物体从系统中“隔离”出来,作为研究对象,分析受力情况,依据牛顿第二定律列方程,如果问题较复杂,涉及未知量较多,只“隔离”一个物体不够,还必须再“隔离”第二个、三个物体等,总的原则是所列方程数与未知量的个数相等就可以了,这种处理连接体问题的思维方法就叫做“隔离法”。
例1. 在探究加速度与力和质量的关系实验中,小车质量200克,小桶质量20克,求绳对小车的拉力多大?若换用50克的钩砝拉此小车,拉力又是多大?
对小桶:mg-T=ma
对小车:T=Ma
解得:T=Mmg/(M+m)
解析:
换用钩砝后,
小桶、小车受力如图
例2. 如图所示,两物块质量为M和m,用绳连接后放在水平面上,物块和水平面间的动摩擦因素为μ,用沿水平面的恒力F拉物块M加速运动,求中间绳子的张力。
由牛顿运动定律:
解:画出M 和m 的受力如图所示:
对M有 F - T - μMg= Ma (1)
对m有 T - μmg= ma (2)
∴a = F/(M+m)-μg (3)
(3)式代入(2)式得
T= mF/( M+m)
例3. 如图所示,两物块质量为M和m,用绳连接后放在倾角为θ的斜面上,物块和斜面的动摩擦因素为μ,用沿斜面向上的恒力F 拉物块M 运动,求中间绳子的张力.
由牛顿运动定律,
解:画出M和m的受力如图:
对M有 F-T-Mgsinθ-μMgcosθ=Ma (1)
对m有 T-mgsinθ-μmgcosθ=ma (2)
∴a =F/(M+m)-gsinθ-μgcosθ (3)
(3)代入(2)式得
T= m(a + gsinθ+μgcosθ) = mF/(M+m)
由上例可知:
T 的大小与运动情况无关
T 的大小与θ无关
T 的大小与μ无关
①两物体加速度不同时,一般使用“隔离法”;
②求两物体之间的拉力,必须使用“隔离法”。
练习1、如图所示,置于水平面上的相同材料的m和M用轻绳连接,在M上施一水平力F(恒力)使两物体作匀加速直线运动,对两物体间细绳拉力正确的说法是: ( )
? (A)水平面光滑时,绳拉力等于mF/(M+m);
(B)水平面不光滑时,绳拉力等于m F/(M+m);
(C)水平面不光滑时,绳拉力大于mF/(M+m);
(D)水平面不光滑时,绳拉力小于mF/(M+m)。
解:由上题结论: T 的大小与μ无关,应选 A B
A B
“整体法”应用专题
例1. 如图所示,两物块质量为M和m,用绳连接后放在水平面上,物块和水平面间的动摩擦因素为μ,用沿水平面的恒力F拉物块M加速运动,求中间绳子的张力。
由牛顿运动定律:
解:
对M+m:F – μ(M+m)g= (M+m)a
对m:T - μmg= ma
∴a = F/(M+m)-μg
T= = mF/( M+m)
例2. 在探究加速度与力和质量的关系实验中,小车质量200克,小桶质量20克,求绳对小车的拉力多大?若换用50克的钩砝拉此小车,拉力又是多大?
对小桶与小车:
对小车:T=Ma=Mmg/(M+m)
解析:
换用钩砝后,
mg=(M+m)a
a=mg/(M+m)
1.连接体或多物体问题优先考虑整体法。
2.整体法往往与隔离法结合使用。
3.整体法的几种情形:
加速度相同时,
加速度相等时,
加速度不等时,
F=(m1+m2)a
F=(m1+m2)a
F=m1a1+m2a2
当a2=0时,F=m1a1
例3. 如图所示,底座A上装有一根直立长杆,其总质量为M,杆上套有质量为m的环B,它与杆有摩擦,当环从底座以初速度向上飞起时(底座保持静止),环的加速度a,求环在升起和下落的过程中,底座对水平面的压力分别为多大?
环和底座的加速度不同,通常应隔离物体分析。
N2=Mg+m(a-g)
环上升时这两个物体的受力如图:
对环: f+mg=ma (1)
对底座:f?+N1-Mg=0 (2)
而 f?=f (3)
对底座:Mg+f?-N2=0 (4)
环下落时环受到的动摩擦力大小不变,环和底座的受力如图:
故 N1=Mg-m(a-g)
由(1)(3)(4)解得:
方法一:隔离法
方法二:整体法
上升时,整体受力如图所示:
(M+m)g-N1=ma
N1=(M+m)g-ma=Mg-m(a-g)
对m:mg+f=ma,f=m(a-g)
下降时,M受力如图所示:
N2=Mg+f?=Mg+f=Mg+m(a-g)
1、本题利用了“程序法”的基本思,划分为两个过程。
2、因加速度不同,本题一般采用“隔离法”分析,但也可利用整体法求解,特别是在求N1时。
例4. 如图所示,质量为m的物体从倾角为θ的光滑斜面上滑下,斜面质量为M, 物体下滑过程中斜面始终静止。求斜面对地面的摩擦力和压力。
解:对物体,加速度沿斜面向下
对M+m,受力如图所示
(M+m)g-F=ma2=masinθ
F=(M+m)g-masin2θ
f=ma1=macosθ=mgsinθcosθ
∴F?= F=(M+m)g-masin2θ,方向竖直向下
f?=f=mgsinθcosθ,方向水平向右
4.6 用牛顿运动定律解决问题(一)
一、牛顿第二定律
内容: 物体的加速度与所受的合力成正比,跟物体的质量成反比,加速度的方向跟合力的方向相同。
教学复习:
数学表达式: F=ma
4.独立性
1.同体性
2.矢量性
3.瞬时性
四性:
速度公式 : vt = vo+at
位移公式: x= vot +0.5at2
导出公式: x=(vt 2- vo 2)/2a
二、运动学知识
教学复习:
动力学的两类基本问题:
1、已知物体的受力情况求物体的运动情况。
2、已知物体的运动情况求物体的受力情况。
例题 1:一个静止在水平地面上的物体,质量是 2kg,在 6.4N的水平拉力作用下沿水平地面向右运动。物体与地面间的摩擦力是4.2N。求物体在4s末的速度和4s内的位移。
问:l、本题研究对象是谁?它共受几个力的作用?物体所受的合力沿什么方向?大小是多少?
2、本题要求计算位移和速度,而我们只会解决匀变速运动问题。这个物体的运动是匀变速运动吗?依据是什么?
3、FN和G在竖直方向上,它们有什么关系?
一、从受力确定运动情况
解:物体受力如右图所示
4s末的速度
4s内的位移
由图知:
说明:解题中求合力的计算式往往和牛二定律结合在一起,而运动学公式单独列出。
解:物体受力如右图所示
4s末的速度
4s内的位移
由图知:
3.利用运动学公式确定物体的运动情况.
解题步骤:
1.确定研究对象,并对物体进行受力分析,弄清题目的物理情景。
2.求出合力,利用牛顿第二定律求出物体的加速度。
例题 2:一个滑雪的人质量是 75 kg,以v0=2m/s的初速度沿山坡匀加速滑下,山坡的倾角θ=30°。在 t=5s的时间内滑下的路程x=60m,求滑雪人受到的阻力(包括摩擦和空气阻力)。
问:1、本题属于那类力学问题?
2、人共受几个力的作用?各力方向如何?
3、它们之中哪个力是已知的?哪个力实际上是己知的?待求力是谁?
4、物体所受的合力沿什么方向?
二、从运动情况确定受力
思路:应先求出加速度a,再利用牛顿第二定律F合=ma求滑雪人受到的阻力。
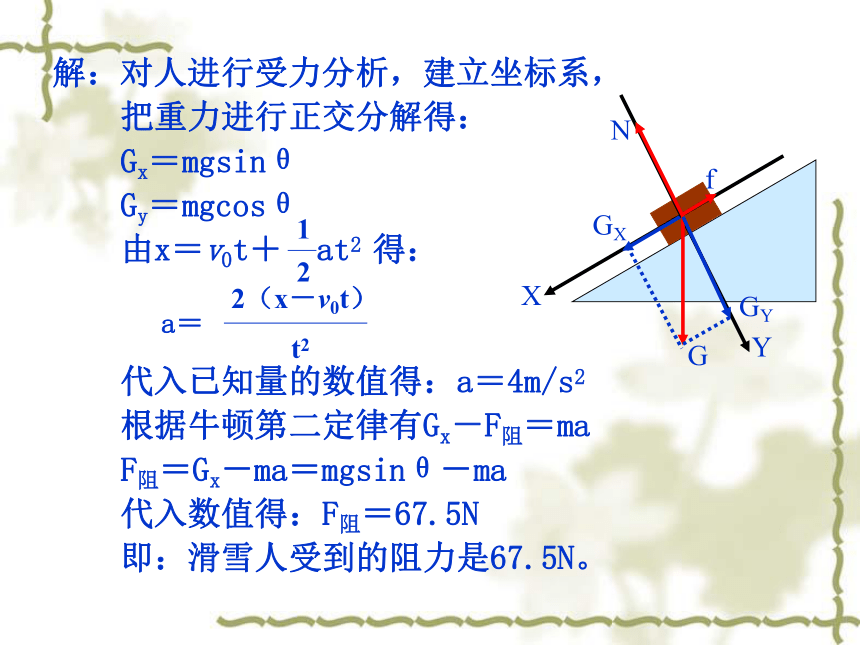
解:对人进行受力分析,建立坐标系,
把重力进行正交分解得:
Gx=mgsinθ
Gy=mgcosθ
由x=v0t+ at2 得:
代入已知量的数值得:a=4m/s2
根据牛顿第二定律有Gx-F阻=ma
F阻=Gx-ma=mgsinθ-ma
代入数值得:F阻=67.5N
即:滑雪人受到的阻力是67.5N。
2.根据物体的运动情况对物体运用运动学公式求出加速度。
解题步骤:
4.结合物体受力分析求出所求的力。
3.根据牛顿第二定律求出合力。
1.对物体进行受力分析并建立题目中的物理情景.
1.已知物体的受力情况求物体的运动情况。
总结:
据
求a
由受力情况求合力
F=ma
求得x,vt,vo等
一、两类问题:
2.已知物体的运动情况求物体的受力情况。
求得a
由运动情况,据
F=ma
求合力
受力分析
求受力情况
总结:
一、两类问题:
说明:两类基本问题中,受力分析是关键,牛二定律是桥梁,求解加速度是枢纽,所以不管是哪一类问题,都要设法先求出加速度。
受力情况F1、F2…
运动情况v0、s…
F合
a
力的合成与分解
牛顿第二定律
运动学公式
总结:
二、常用方法:
1.多物体问题
2.多力问题
3.多过程问题
按顺序对题目给出的物体运动过程进行分段分析的方法简称“程序法”。“程序法”要求从读题开始,就要注意题中含有多少个不同的过程或多少个不同的状态,然后对各个过程或各个状态进行分析。
——隔离法
——正交分解法
——程序法
练习:
质量为1.5Kg的物体在与水平面成37。角的拉力F为10N的力的作用下,沿着水平桌面向右做匀加速直线运动,经过一段距离,速度由5m/s变为7m/s,已知物体与桌面的摩擦力大小为5N,求物体通过的距离。
(cos 37。=0.8,sin 37。=0.6)
V0=5m/s
Vt=7m/s
已知:m=1.5kg,f=5N,g=10m/s2,F=10N,θ=37,Vt= 7m/s V0=5m/s
求: x
) θ
解:物体受到四个力的作用,如图所示。由于物体沿水平面运动,固建立如图所示的直角坐标系
x轴方向:Fcosθ-f = F合
y轴方向:Fsinθ+ F支= mg
解此方程组可得: F合 =3N
所以:a= F合 /m=2m/s2
又由公式:x=(vt2-vo2)/2a
解得:x=6m
正交分解法应用专题
所谓正交分解法是把一个矢量分解在两个互相垂直的坐标轴上的方法。
正交分解法是一种常用的矢量运算方法,也是解牛顿第二定律题目最基本的方法。物体在受到三个或三个以上的不在同一直线上的力的作用时一般都采用正交分解法。
表示方法:
建立坐标系时确定x轴的正方向一般有两种方法:
(1)分解力而不分解加速度,此时应规定加速度的方向为x轴的正方向。
(2)分解加速度而不分解力,此法一般是以某个力的方向为x轴的正方向,而其它力都落在两坐标上而不需要再分解,或者加速度已知分解方便。
1.质量为的三角形木块A置于倾角为θ的固定斜面上,它与斜面间的动摩擦因数为μ,一水平力F的推动下, 木块A沿斜面以恒定的加速度a向上滑动,如图甲所示,则力F的大小为多少?
将物体所受各力沿平行斜面方向和
垂直斜面方向正交分解,不分解加速
度,如图所示,即可得出方程组:
垂直斜面方向上有:
2.一物体放置在倾角为为θ的斜面上,斜面固定在加速上升的电梯中,加速度为a,如图所示,在物体始终相对于斜面静止的情况下,下列说法正确的是:( )
A.当θ一定时,a越大,斜面对物体的正压力越小;
B.当θ一定时,a越大,斜面对物体的摩擦力越大;
C.当a一定时,θ越大,斜面对物体的正压力越小;
D.当a一定时,θ越大,斜面对物体的摩擦力越小。
选物体为研究对象,受力如图所示,建立坐标系,注意题中物体相对于斜面静止,所以f是静摩擦力,加速度向上,所以静摩擦力f沿斜面向上。
水平方向:
当θ一定时,a变大,N、f均变大。
当a一定时,θ变大,N越小,f越大。
竖直方向:
方法1.正交分解法
方法2.合成法
当θ一定时,a变大,N、f均变大。
当a一定时,θ变大,N越小,f越大。
3.如图所示,质量为M的人站在自动扶梯上,扶梯正在以加速度a斜向上做匀减速运动,a与水平方向夹角为θ,求人受到的摩擦力和支持力?
a
物体在受到三个或三个以上的不同方向的力作用时,一般都要用到正交分解法。在建立坐标系时,不管选取哪个方向为X轴的正方向时,所得的最后结果都应是一样的。在选取坐标轴时,为使解题方便,应考虑尽量减少矢量的分解,若已知加速度方向一般以加速度方向为正方向。
“程序法” 应用专题
按顺序对题目给出的物体运动过程进行分段分析的方法简称”程序法”,“程序法”要求从读题开始,就要注意题中含有多少个不同的过程或多少个不同的状态,然后对各个过程或各个状态进行分析。
1.物体在粗糙斜面的底端O以初速V沿斜面上滑,到最高点P后又滑回到O点,那么:
A.它上滑和下滑过程中加速度的方向相同;
B.它的上滑时间比下滑时间长;
C.它在P点时速度和加速度都等于零;
D.它滑回到O点时速率一定小于v。
v
利用”逆向法”列运动学公式得:
(2)过程二:匀加速下滑,受力如图。
由牛顿第二定律得:
由运动学公式得:
(1)过程一:匀减速上滑,受力如图.
由牛顿第二定律得:
题目描述有两个过程:
1.物体在粗糙斜面的底端O以初速V沿斜面上滑,到最高点P后又滑回到O点,那么:
A.它上滑和下滑过程中加速度的方向相同;
B.它的上滑时间比下滑时间长;
C.它在P点时速度和加速度都等于零;
D.它滑回到O点时速率一定小于v。
v
比较①④式得:
比较②⑤式得:
比较③⑥式得:
B错,D对
物体在P点能滑下,
在P点合力不为零,即在P点
由分析可知,加速度均沿斜面向下
A对,C错
A、D
2、如图所示,一个弹簧台秤的秤盘的质量和弹簧的质量都不计,盘内放一个物体P处于静止,P的质量m=12kg,弹簧的劲度系数k=800N/m。现在给P施加一个竖直向上的力F,使P从静止开始向上做匀加速直线运动,已知在t=0.2s内F是变力,t=0.2s以后F是恒力,g=10m/s2,求F的最小值和最大值。
P
F
此题包括含有三个状态或过程:P静止→P压紧托盘(弹簧)向上匀加速→P离开托盘向上匀加速。
(1)过程一:弹簧被压缩x0,P静止。受力如右图甲所示,由平衡条件得:
(2)过程二:P压紧托盘(弹簧)向上匀加速,受力如右图乙所示,此一过程可用极限分析法分析:
∵向上得合力不变,∴在最低点时,向上的弹力最大,故向上的拉力必最小;物体与秤盘分离时,弹簧弹力最小(为0),故向上的拉力最大。
(3)过程三:t=0.2s后,物体离开托盘,F为恒力。
在最低点:
在最高点:
P静止在盘内时,受力如右图甲所示,
由平衡条件得:
解:
P压紧托盘(弹簧)向上匀加速,受力如右图乙所示,
②“过程二”是动态变化过程,利用“极限法”思想推向两个极端,找出最大值、最小值的条件。“程序法”和“极限法”是分析复杂过程得常用方法。
①此题要按“程序法”划分为三个阶段分析才能把整个过程得隐含条件挖掘出来。
练习、如图所示,自由下落的小球下落一段时间后与弹簧接触,从它接触弹簧开始,到弹簧压缩到最短的过程中,小球的速度、加速度、合外力的变化情况是怎样的?
“隔离法”应用专题
在连接体中把某个物体从系统中“隔离”出来,作为研究对象,分析受力情况,依据牛顿第二定律列方程,如果问题较复杂,涉及未知量较多,只“隔离”一个物体不够,还必须再“隔离”第二个、三个物体等,总的原则是所列方程数与未知量的个数相等就可以了,这种处理连接体问题的思维方法就叫做“隔离法”。
例1. 在探究加速度与力和质量的关系实验中,小车质量200克,小桶质量20克,求绳对小车的拉力多大?若换用50克的钩砝拉此小车,拉力又是多大?
对小桶:mg-T=ma
对小车:T=Ma
解得:T=Mmg/(M+m)
解析:
换用钩砝后,
小桶、小车受力如图
例2. 如图所示,两物块质量为M和m,用绳连接后放在水平面上,物块和水平面间的动摩擦因素为μ,用沿水平面的恒力F拉物块M加速运动,求中间绳子的张力。
由牛顿运动定律:
解:画出M 和m 的受力如图所示:
对M有 F - T - μMg= Ma (1)
对m有 T - μmg= ma (2)
∴a = F/(M+m)-μg (3)
(3)式代入(2)式得
T= mF/( M+m)
例3. 如图所示,两物块质量为M和m,用绳连接后放在倾角为θ的斜面上,物块和斜面的动摩擦因素为μ,用沿斜面向上的恒力F 拉物块M 运动,求中间绳子的张力.
由牛顿运动定律,
解:画出M和m的受力如图:
对M有 F-T-Mgsinθ-μMgcosθ=Ma (1)
对m有 T-mgsinθ-μmgcosθ=ma (2)
∴a =F/(M+m)-gsinθ-μgcosθ (3)
(3)代入(2)式得
T= m(a + gsinθ+μgcosθ) = mF/(M+m)
由上例可知:
T 的大小与运动情况无关
T 的大小与θ无关
T 的大小与μ无关
①两物体加速度不同时,一般使用“隔离法”;
②求两物体之间的拉力,必须使用“隔离法”。
练习1、如图所示,置于水平面上的相同材料的m和M用轻绳连接,在M上施一水平力F(恒力)使两物体作匀加速直线运动,对两物体间细绳拉力正确的说法是: ( )
? (A)水平面光滑时,绳拉力等于mF/(M+m);
(B)水平面不光滑时,绳拉力等于m F/(M+m);
(C)水平面不光滑时,绳拉力大于mF/(M+m);
(D)水平面不光滑时,绳拉力小于mF/(M+m)。
解:由上题结论: T 的大小与μ无关,应选 A B
A B
“整体法”应用专题
例1. 如图所示,两物块质量为M和m,用绳连接后放在水平面上,物块和水平面间的动摩擦因素为μ,用沿水平面的恒力F拉物块M加速运动,求中间绳子的张力。
由牛顿运动定律:
解:
对M+m:F – μ(M+m)g= (M+m)a
对m:T - μmg= ma
∴a = F/(M+m)-μg
T= = mF/( M+m)
例2. 在探究加速度与力和质量的关系实验中,小车质量200克,小桶质量20克,求绳对小车的拉力多大?若换用50克的钩砝拉此小车,拉力又是多大?
对小桶与小车:
对小车:T=Ma=Mmg/(M+m)
解析:
换用钩砝后,
mg=(M+m)a
a=mg/(M+m)
1.连接体或多物体问题优先考虑整体法。
2.整体法往往与隔离法结合使用。
3.整体法的几种情形:
加速度相同时,
加速度相等时,
加速度不等时,
F=(m1+m2)a
F=(m1+m2)a
F=m1a1+m2a2
当a2=0时,F=m1a1
例3. 如图所示,底座A上装有一根直立长杆,其总质量为M,杆上套有质量为m的环B,它与杆有摩擦,当环从底座以初速度向上飞起时(底座保持静止),环的加速度a,求环在升起和下落的过程中,底座对水平面的压力分别为多大?
环和底座的加速度不同,通常应隔离物体分析。
N2=Mg+m(a-g)
环上升时这两个物体的受力如图:
对环: f+mg=ma (1)
对底座:f?+N1-Mg=0 (2)
而 f?=f (3)
对底座:Mg+f?-N2=0 (4)
环下落时环受到的动摩擦力大小不变,环和底座的受力如图:
故 N1=Mg-m(a-g)
由(1)(3)(4)解得:
方法一:隔离法
方法二:整体法
上升时,整体受力如图所示:
(M+m)g-N1=ma
N1=(M+m)g-ma=Mg-m(a-g)
对m:mg+f=ma,f=m(a-g)
下降时,M受力如图所示:
N2=Mg+f?=Mg+f=Mg+m(a-g)
1、本题利用了“程序法”的基本思,划分为两个过程。
2、因加速度不同,本题一般采用“隔离法”分析,但也可利用整体法求解,特别是在求N1时。
例4. 如图所示,质量为m的物体从倾角为θ的光滑斜面上滑下,斜面质量为M, 物体下滑过程中斜面始终静止。求斜面对地面的摩擦力和压力。
解:对物体,加速度沿斜面向下
对M+m,受力如图所示
(M+m)g-F=ma2=masinθ
F=(M+m)g-masin2θ
f=ma1=macosθ=mgsinθcosθ
∴F?= F=(M+m)g-masin2θ,方向竖直向下
f?=f=mgsinθcosθ,方向水平向右
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
