2018-2019学年河北省邯郸市临漳县八年级(上)期末数学试卷(解析版)
文档属性
| 名称 | 2018-2019学年河北省邯郸市临漳县八年级(上)期末数学试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 669.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 07:06:24 | ||
图片预览



文档简介
2018-2019学年河北省邯郸市临漳县八年级(上)期末数学试卷
一、选择题(共16小题;共48分)
1.下列命题中,真命题是( )
A.两个锐角的和一定是钝角
B.相等的角是对顶角
C.带根号的数一定是无理数
D.垂线段最短
2.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为( )
A.(3,0) B.(﹣3,0) C.(a,0) D.(﹣b,0)
3.一次函数y=﹣x的图象平分( )
A.第一、三象限 B.第一、二象限
C.第二、三象限 D.第二、四象限
4.若=成立,则x的取值范围为( )
A.x≥0 B.0≤x<1 C.x<1 D.x≥0或x<1
5.在﹣1、0、1、2这四个数中,最小的数是( )
A.﹣1 B.0 C.1 D.1
6.已知二元一次方程x+7y=5,用含x的代数式表示y,正确的是( )
A. B. C.5+7y D.5﹣7y
7.已知a=,b=,则=( )
A.2a B.ab C.a2b D.ab2
8.把化为最简二次根式得( )
A. B. C. D.
9.如图,数轴上的四个点A,B,C,D对应的数为整数,且AB=BC=CD=1,若|a|+|b|=2,则原点的位置可能是( )
A.A或B B.B或C C.C或D D.D或A
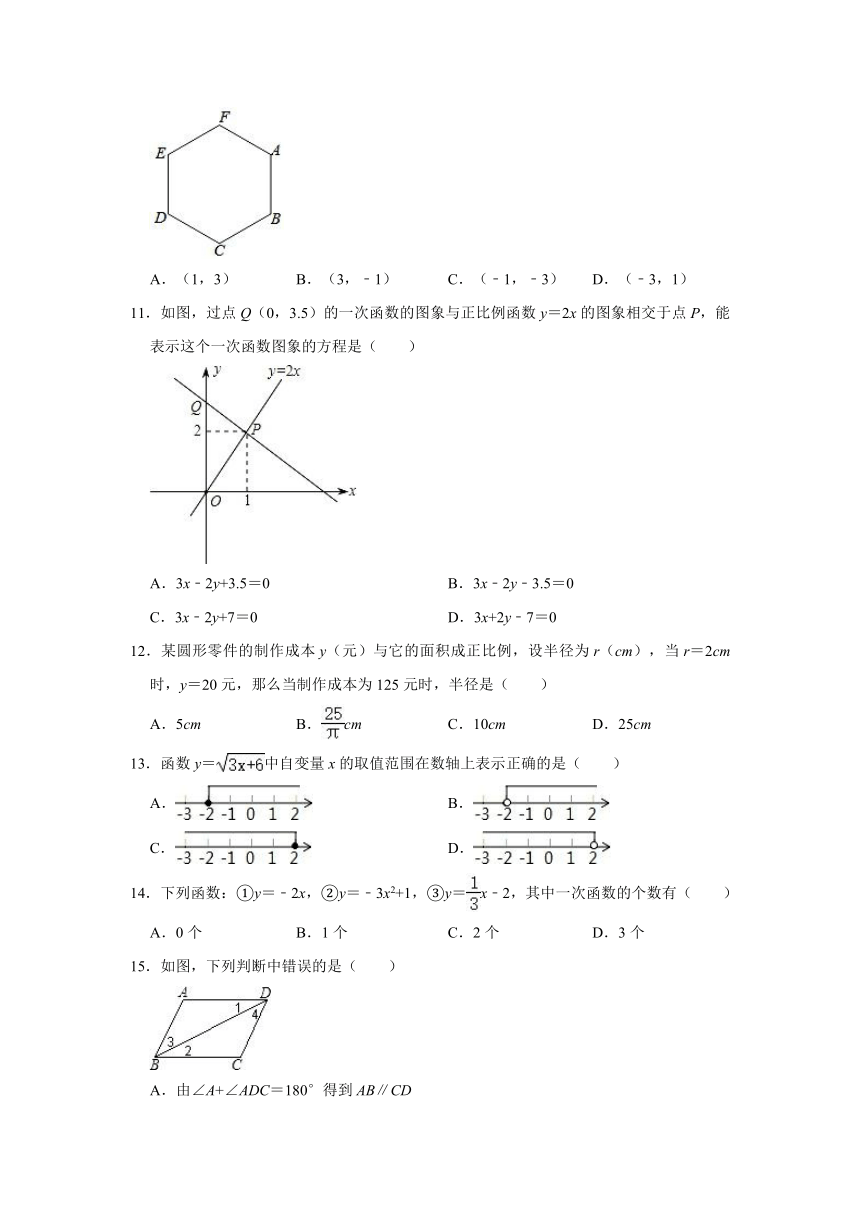
10.如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( )
A.(1,3) B.(3,﹣1) C.(﹣1,﹣3) D.(﹣3,1)
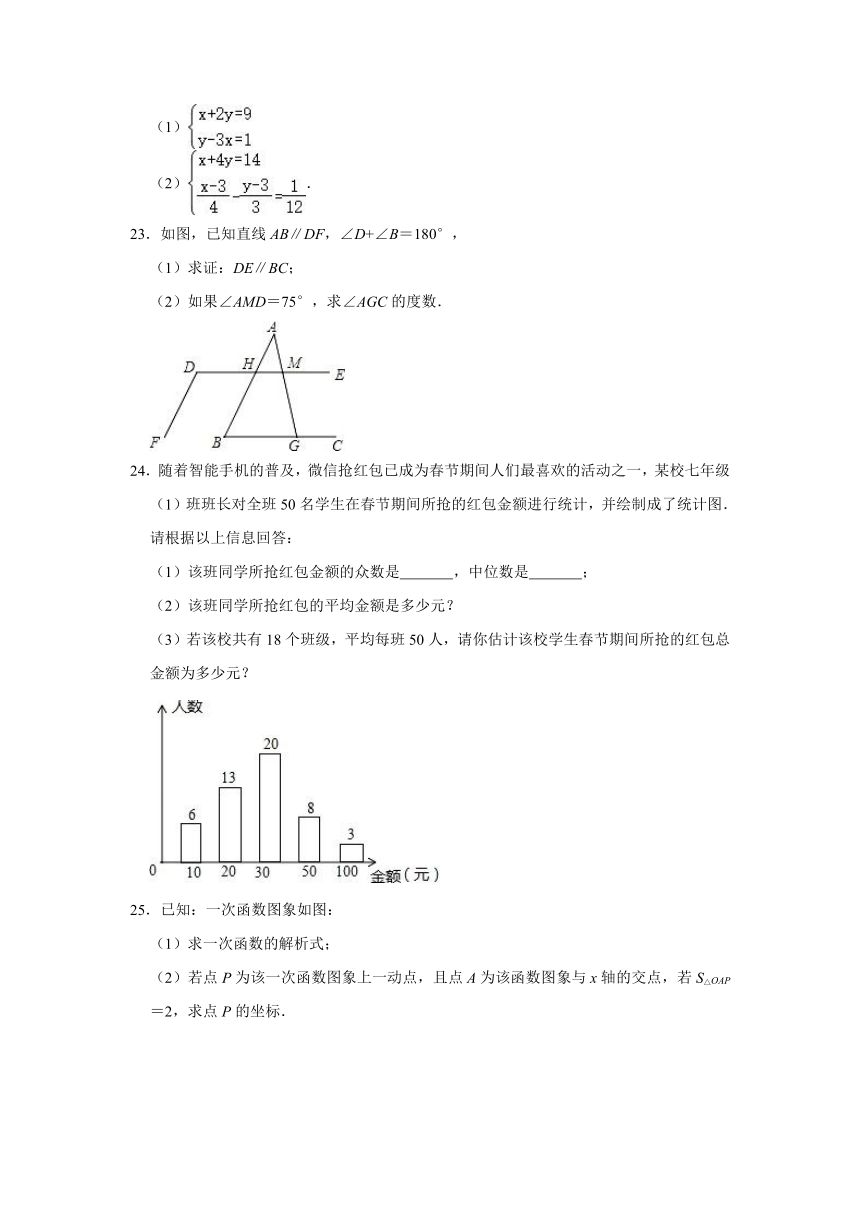
11.如图,过点Q(0,3.5)的一次函数的图象与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的方程是( )
A.3x﹣2y+3.5=0 B.3x﹣2y﹣3.5=0
C.3x﹣2y+7=0 D.3x+2y﹣7=0
12.某圆形零件的制作成本y(元)与它的面积成正比例,设半径为r(cm),当r=2cm时,y=20元,那么当制作成本为125元时,半径是( )
A.5cm B.cm C.10cm D.25cm
13.函数y=中自变量x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
14.下列函数:①y=﹣2x,②y=﹣3x2+1,③y=x﹣2,其中一次函数的个数有( )
A.0个 B.1个 C.2个 D.3个
15.如图,下列判断中错误的是( )
A.由∠A+∠ADC=180°得到AB∥CD
B.由AB∥CD得到∠ABC+∠C=180°
C.由∠1=∠2得到AD∥BC
D.由AD∥BC得到∠3=∠4
16.古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
A.13=3+10 B.25=9+16 C.36=15+21 D.49=18+31
二、填空题(共4小题;共3x4=12分)
17.已知:,则x+y+z= .
18.已知是二元一次方程组的解,则3m﹣n的值为 .
19.某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是 .
20.已知:x=,y=.那么+= .
三、解答题(共6小题;共60分)
21.计算:
(1)2+3;
(2)
22.解方程组:
(1)
(2).
23.如图,已知直线AB∥DF,∠D+∠B=180°,
(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
24.随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.
请根据以上信息回答:
(1)该班同学所抢红包金额的众数是 ,中位数是 ;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
25.已知:一次函数图象如图:
(1)求一次函数的解析式;
(2)若点P为该一次函数图象上一动点,且点A为该函数图象与x轴的交点,若S△OAP=2,求点P的坐标.
26.某市为了鼓励居民节约用水,决定实行两级收费制度,若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价m和市场价n分别是多少元?
(2)小明家5月份交水费70元,则5月份他家用了多少吨水?
2018-2019学年河北省邯郸市临漳县八年级(上)期末数学试卷
参考答案与试题解析
一、选择题(共16小题;共48分)
1.下列命题中,真命题是( )
A.两个锐角的和一定是钝角
B.相等的角是对顶角
C.带根号的数一定是无理数
D.垂线段最短
【解答】解:30°+30°=60°,故选项A中的命题是假命题;
相等的角不一定是对顶角,只要度数相等就是相等的角,故选项B中的命题是假命题;
,故选项C中的命题是假命题;
垂线段最短,故选项D中的命题是真命题;
故选:D.
2.一元一次方程ax﹣b=0的解x=3,函数y=ax﹣b的图象与x轴的交点坐标为( )
A.(3,0) B.(﹣3,0) C.(a,0) D.(﹣b,0)
【解答】解:∵一元一次方程ax﹣b=0的解x=3,
∴函数y=ax﹣b的图象与x轴的交点坐标为(3,0),
故选:A.
3.一次函数y=﹣x的图象平分( )
A.第一、三象限 B.第一、二象限
C.第二、三象限 D.第二、四象限
【解答】解:∵k=﹣1<0,
∴一次函数y=﹣x的图象经过二、四象限,
∴一次函数y=﹣x的图象平分二、四象限.
故选:D.
4.若=成立,则x的取值范围为( )
A.x≥0 B.0≤x<1 C.x<1 D.x≥0或x<1
【解答】解:由题意知,
解得:0≤x<1,
故选:B.
5.在﹣1、0、1、2这四个数中,最小的数是( )
A.﹣1 B.0 C.1 D.1
【解答】解:根据有理数比较大小的方法,可得
﹣1<0<1<2,
∴在﹣1、0、1、2这四个数中,最小的数是﹣1.
故选:A.
6.已知二元一次方程x+7y=5,用含x的代数式表示y,正确的是( )
A. B. C.5+7y D.5﹣7y
【解答】解:∵x+7y=5,
∴7y=﹣x+5,
则y=,
故选:B.
7.已知a=,b=,则=( )
A.2a B.ab C.a2b D.ab2
【解答】解:==××=a?b?b=ab2.
故选:D.
8.把化为最简二次根式得( )
A. B. C. D.
【解答】解:原式=,
故选:C.
9.如图,数轴上的四个点A,B,C,D对应的数为整数,且AB=BC=CD=1,若|a|+|b|=2,则原点的位置可能是( )
A.A或B B.B或C C.C或D D.D或A
【解答】解:∵AB=BC=CD=1,
∴当点A为原点时,|a|+|b|>2,不合题意;
当点B为原点时,|a|+|b|=2,符合题意;
当点C为原点时,|a|+|b|=2,符合题意;
当点D为原点时,|a|+|b|>2,不合题意;
故选:B.
10.如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(﹣a,b),则点D的坐标为( )
A.(1,3) B.(3,﹣1) C.(﹣1,﹣3) D.(﹣3,1)
【解答】解:如图,由点A、E的坐标分别为(a,b)、(﹣a,b)知A、E两点关于y轴对称,
则B、D两点也关于y轴对称,
∵B(3,1),
∴D(﹣3,1),
故选:D.
11.如图,过点Q(0,3.5)的一次函数的图象与正比例函数y=2x的图象相交于点P,能表示这个一次函数图象的方程是( )
A.3x﹣2y+3.5=0 B.3x﹣2y﹣3.5=0
C.3x﹣2y+7=0 D.3x+2y﹣7=0
【解答】解:设这个一次函数的解析式为y=kx+b.
∵这条直线经过点P(1,2)和点Q(0,3.5),
∴,
解得.
故这个一次函数的解析式为y=﹣1.5x+3.5,
即:3x+2y﹣7=0.
故选:D.
12.某圆形零件的制作成本y(元)与它的面积成正比例,设半径为r(cm),当r=2cm时,y=20元,那么当制作成本为125元时,半径是( )
A.5cm B.cm C.10cm D.25cm
【解答】解:设y与r之间的函数关系式为y=kπr2,由题意,得
20=4πk,
解得:k=,
∴y=5r2,
当y=125时,125=5r2,
∴r=5.
故选:A.
13.函数y=中自变量x的取值范围在数轴上表示正确的是( )
A. B.
C. D.
【解答】解:由函数y=,得到3x+6≥0,
解得:x≥﹣2,
表示在数轴上,如图所示:
故选:A.
14.下列函数:①y=﹣2x,②y=﹣3x2+1,③y=x﹣2,其中一次函数的个数有( )
A.0个 B.1个 C.2个 D.3个
【解答】解:①y=﹣2x是正比例函数,也是一次函数,②y=﹣3x2+1是二次函数,③y=x﹣2是一次函数.
故选:C.
15.如图,下列判断中错误的是( )
A.由∠A+∠ADC=180°得到AB∥CD
B.由AB∥CD得到∠ABC+∠C=180°
C.由∠1=∠2得到AD∥BC
D.由AD∥BC得到∠3=∠4
【解答】解:A、由∠A+∠ADC=180°得到AB∥CD(同旁内角互补,两直线平行),正确;
B、由AB∥CD得到∠ABC+∠C=180°(两直线平行,同旁内角互补),正确;
C、由∠1=∠2得到AD∥BC(内错角相等,两直线平行),正确;
D、由AD∥BC得到∠1=∠2(两直线平行,内错角相等),所以此选项错误.
故选:D.
16.古希腊著名的毕达哥拉斯学派把1,3,6,10…这样的数称为“三角形数”,而把1,4,9,16…这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )
A.13=3+10 B.25=9+16 C.36=15+21 D.49=18+31
【解答】解:显然选项A中13不是“正方形数”;选项B、D中等式右侧并不是两个相邻“三角形数”之和.
故选:C.
二、填空题(共4小题;共3x4=12分)
17.已知:,则x+y+z= 6 .
【解答】解:三个式子相加得:2(x+y+z)=12,
则x+y+z=6.
故答案是:6.
18.已知是二元一次方程组的解,则3m﹣n的值为 7 .
【解答】解:由题意可得:
,
解得:,
故3m﹣n=9﹣2=7.
故答案为:7.
19.某班学生参加环保知识竞赛,已知竞赛得分都是整数.把参赛学生的成绩整理后分为6小组,画出竞赛成绩的频数分布直方图(如图所示),根据图中的信息,可得成绩高于60分的学生占全班参赛人数的百分率是 80% .
【解答】解:∵全班的总人数为3+6+12+11+7+6=45人,其中成绩高于60分的学生有12+11+7+6=36人,
∴成绩高于60分的学生占全班参赛人数的百分率是×100%=80%,
故答案为:80%.
20.已知:x=,y=.那么+= 98 .
【解答】解:∵x==5﹣2,y==5+2,
∴原式===98,
故答案为:98
三、解答题(共6小题;共60分)
21.计算:
(1)2+3;
(2)
【解答】解:(1)原式=4+12
=16;
(2)原式=×2+×2
=+2
=.
22.解方程组:
(1)
(2).
【解答】解:(1),
由②得,y=3x+1③,
③代入①得,x+2(3x+1)=9,
解得x=1,
把x=1代入③得,y=3+1=4,
所以,方程组的解是;
(2)方组可化为,
①+②得,4x=12,
解得x=3,
把x=3代入①得,3+4y=14,
解得y=,
所以,原方程组的解是.
23.如图,已知直线AB∥DF,∠D+∠B=180°,
(1)求证:DE∥BC;
(2)如果∠AMD=75°,求∠AGC的度数.
【解答】(1)证明:∵AB∥DF,
∴∠D+∠BHD=180°,
∵∠D+∠B=180°,
∴∠B=∠DHB,
∴DE∥BC;
(2)解:∵DE∥BC,∠AMD=75°,
∴∠AGB=∠AMD=75°,
∴∠AGC=180°﹣∠AGB=180°﹣75°=105°.
24.随着智能手机的普及,微信抢红包已成为春节期间人们最喜欢的活动之一,某校七年级(1)班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.
请根据以上信息回答:
(1)该班同学所抢红包金额的众数是 30 ,中位数是 30 ;
(2)该班同学所抢红包的平均金额是多少元?
(3)若该校共有18个班级,平均每班50人,请你估计该校学生春节期间所抢的红包总金额为多少元?
【解答】解:(1)捐款30元的人数为20人,最多,则众数为30,
中间两个数分别为30和30,则中位数是30.
故答案为30,30;
(2)该班同学所抢红包的平均金额是(6×10+13×20+20×30+8×50+3×100)÷50=32.4(元);
(3)18×50×32.4=29160(元).
答:估计该校学生春节期间所抢的红包总金额为29160元.
25.已知:一次函数图象如图:
(1)求一次函数的解析式;
(2)若点P为该一次函数图象上一动点,且点A为该函数图象与x轴的交点,若S△OAP=2,求点P的坐标.
【解答】解:(1)设一次函数解析式为y=kx+b,
把(﹣2,3)、(2,﹣1)分别代入得,解得,
所以一次函数解析式为y=﹣x+1;
(2)当y=0时,﹣x+1=0,解得x=1,则A(1,0),
设P(t,﹣t+1),
因为S△OAP=2,
所以×1×|﹣t+1|=2,解得t=﹣3或t=5,
所以P点坐标为(﹣3,4)或(5,﹣4).
26.某市为了鼓励居民节约用水,决定实行两级收费制度,若每月用水量不超过14吨(含14吨),则每吨按政府补贴优惠价m元收费;若每月用水量超过14吨,则超过部分每吨按市场价n元收费.小明家3月份用水20吨,交水费49元;4月份用水18吨,交水费42元.
(1)求每吨水的政府补贴优惠价m和市场价n分别是多少元?
(2)小明家5月份交水费70元,则5月份他家用了多少吨水?
【解答】解:(1)根据题意得:,
解得:.
答:每吨水的政府补贴优惠价m是2元,市场价n是3.5元.
(2)设5月份小明家用了x吨水,
根据题意得:14×2+3.5(x﹣14)=70,
解得:x=26.
答:5月份小明家用了26吨水.
同课章节目录
