4.2.1直线与圆的位置关系[1](共33张PPT)
文档属性
| 名称 | 4.2.1直线与圆的位置关系[1](共33张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 736.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 15:29:42 | ||
图片预览









文档简介
(共33张PPT)
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报;台风中心位于轮船正西70km处,受影响的范围是半径长为30km的圆形区域.已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
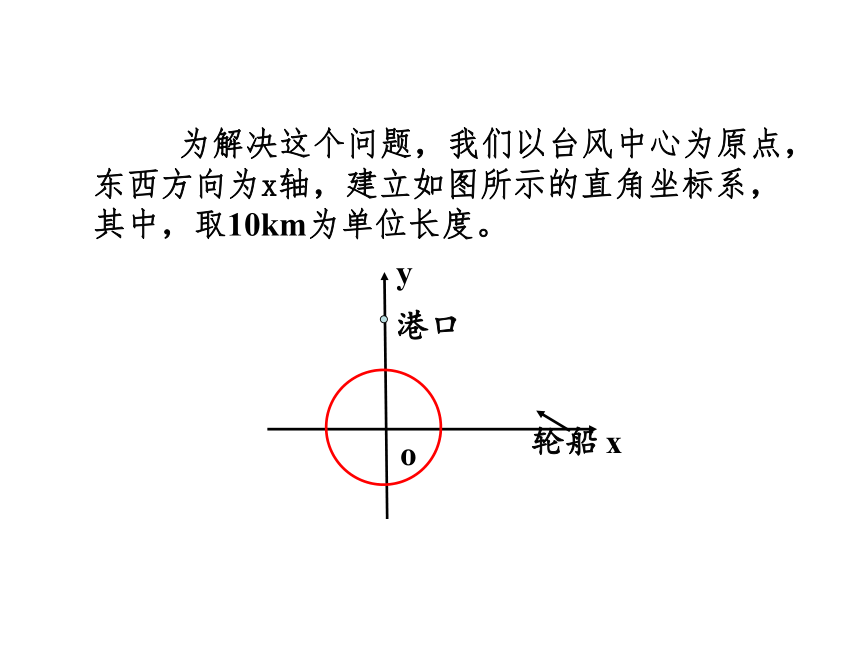
为解决这个问题,我们以台风中心为原点,东西方向为x轴,建立如图所示的直角坐标系,其中,取10km为单位长度。
这样,受台风影响的圆形区域对应的圆心为O的圆的方程为
轮船航线所在直线l 的方程为
问题归结为圆心为O的圆与直线 l 有无公共点。
4.2.1 直线与圆的位置关系
理解直线与圆的位置的种类。
利用平面直角坐标系中点到直线的距离公式求圆心到直线的距离。
会用点到直线的距离来判断直线与圆的位置关系。
让学生通过观察图形,理解并掌握直线与圆的位置关系,培养学生数形结合的思想。
设直线,圆,圆的半径为,圆心到直线的距离为,则:
(1)当时,直线与圆相离;
(2)当时,直线与圆相切;
(3)当时,直线与圆相交。
用坐标法判直线与圆的位置关系。
直线与圆的位置关系的几何图形及其判断方法。
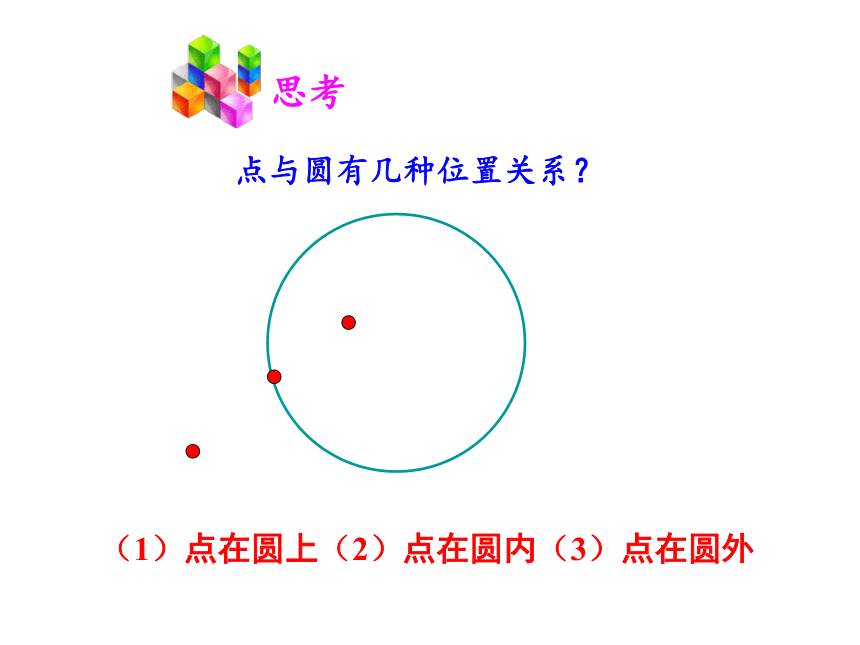
点与圆有几种位置关系?
(1)点在圆上(2)点在圆内(3)点在圆外
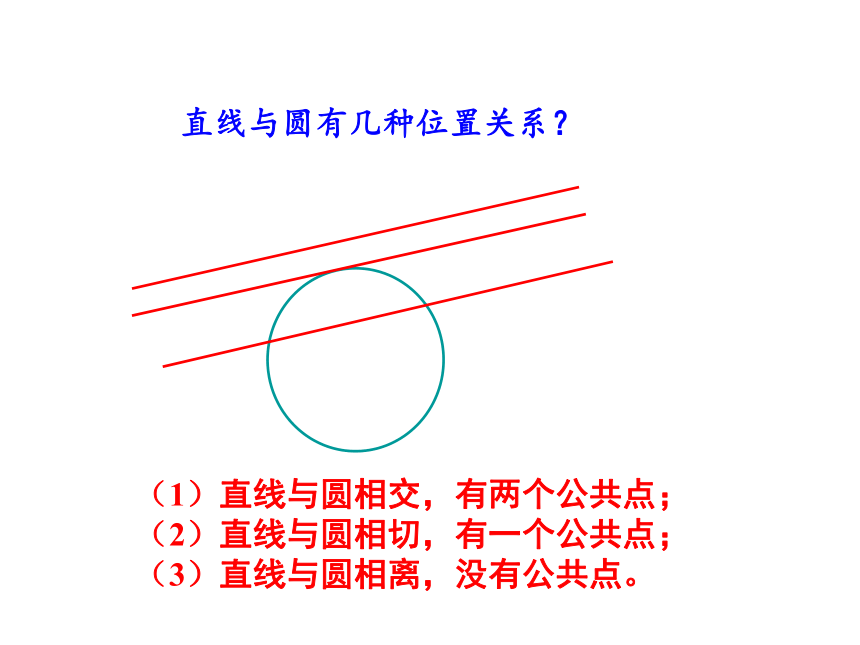
直线与圆有几种位置关系?
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,有一个公共点;
(3)直线与圆相离,没有公共点。
直线与圆有_____种位置关系,是用直线与圆的________的个数来定义的.这也是判断直线与圆的位置关系的重要方法。
三
公共点
如何判断直线与圆的位置关系?
(1)直线l和 ⊙O相交〈==〉有两个公共点;
(2)直线l和 ⊙O相切〈==〉一个公共点;
(3)直线l和 ⊙O相离〈==〉没有公共点。
如果⊙O的半径为 r,圆心O到直线 l的距离为d,
(1)直线 l 和 ⊙O相交〈==〉d < r;
(2)直线 l 和 ⊙O相切〈==〉d = r;
(3)直线 l 和 ⊙O相离〈==〉d > r。
联立直线l 与圆O的方程,
(1)如果有两组实数解,直线与圆相交;
(2)如果有一组实数解,直线与圆相切;
(3)如果没有实数解,直线与相离。
已知圆的方程是 ,直线方程 当b取何值时,直线与圆相交;相切;相离。
解法1:
根据题意得:
当直线与圆相切时,直线与圆有一个交点。
当直线与圆相离时,直线与圆有没有交点。
当直线与圆相交时,直线与圆有两个交点。
解法2:
圆心O到直线y=x+b的距离d为
当直线与圆相交时,d < r
当直线与圆相切时,d = r
当直线与圆相离时,d > r
已知点P(5,0)和⊙O:x2+y2=16
(1)自P作⊙O的切线,求切线的长及切线的方程;
(2)过P任意作直线l与⊙O交于A、B两相异点,求弦AB中点M的轨迹。
解:(1)设过P的圆O的切线切圆于点Q,
∵△PQO是直角三角形 ,
∴切线长PQ=
连OQ,
Q
(2)设M(x,y)是所求轨迹上任一点,A(x1,y1),B(x2,y2)
AB的斜率为k,
1
Δ= 0
1根
d = r
2
Δ> 0
2根
d < r
0
Δ< 0
无根
d > r
示意图形 交点个数 方程组消元后 圆心到直线d与r关系
相切
相交
相离
1.(2009 重庆)直线 与圆
的位置关系是( )
A.相切 B.相交但直线不过圆心C.直线过圆心 D.相离
B
【解析】圆心(0,0)到直线 的距
离 ,而
2.(2007 安徽)若圆
的圆心到直线 的距离为
则a的值为( )
-2或2 B. 或 C. 2或0 D. -2或0
C
【解析】易知圆心是(1,2),由
可解得a=2或0
1.对任意实数k,圆C: x2+y2-6x-8y+12=0与直线L:kx-y-4k+3=0的位置关系是( )
A 相交 B相切 C相离 D与k值有关
A
2.若直线ax+by=1与圆x2+y2=1相交,则点P(a,b)与圆的位置关系是( )
A. 在圆上 B. 在圆内
C. 在圆外 D. 以上皆有可能
C
3.若圆x2+y2=1与直线 (a>0,b>0)相切,
则ab的最小值为( )
C
4.如图,已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。
由直线l与圆的方程,得:
消去y,得:
因为:
= 1 > 0
所以,直线 l 与圆相交,有两个公共点。
所以,直线 l 与圆有两个交点,它们的坐标分别是:
A(2,0),B(1,3)
1.解:以台风中心为原点O,东西方向为x轴,建立直角坐标系,其中,取10km为单位长度。
这样,受台风影响的圆形区域所对应的圆O方程为
轮船航线AB所在直线l的方程为
4x+7y-28=0
问题归结为圆O与直线l有无公共点。
点O到直线l的距离
圆O的半径长r=3。
因为3.5>3,所以这艘轮船不必改变航线,不会受到台风的影响。
2.解:因为原点O到直线4x+3y-35=0的距离
圆心在原点,与直线4x+3y-35=0相切的圆C方程是
圆心坐标是(1,0),半径长r=1。
圆心到直线3x+4y+2=0的距离
所以直线l与圆C无公共点。
一艘轮船在沿直线返回港口的途中,接到气象台的台风预报;台风中心位于轮船正西70km处,受影响的范围是半径长为30km的圆形区域.已知港口位于台风中心正北40km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
为解决这个问题,我们以台风中心为原点,东西方向为x轴,建立如图所示的直角坐标系,其中,取10km为单位长度。
这样,受台风影响的圆形区域对应的圆心为O的圆的方程为
轮船航线所在直线l 的方程为
问题归结为圆心为O的圆与直线 l 有无公共点。
4.2.1 直线与圆的位置关系
理解直线与圆的位置的种类。
利用平面直角坐标系中点到直线的距离公式求圆心到直线的距离。
会用点到直线的距离来判断直线与圆的位置关系。
让学生通过观察图形,理解并掌握直线与圆的位置关系,培养学生数形结合的思想。
设直线,圆,圆的半径为,圆心到直线的距离为,则:
(1)当时,直线与圆相离;
(2)当时,直线与圆相切;
(3)当时,直线与圆相交。
用坐标法判直线与圆的位置关系。
直线与圆的位置关系的几何图形及其判断方法。
点与圆有几种位置关系?
(1)点在圆上(2)点在圆内(3)点在圆外
直线与圆有几种位置关系?
(1)直线与圆相交,有两个公共点;
(2)直线与圆相切,有一个公共点;
(3)直线与圆相离,没有公共点。
直线与圆有_____种位置关系,是用直线与圆的________的个数来定义的.这也是判断直线与圆的位置关系的重要方法。
三
公共点
如何判断直线与圆的位置关系?
(1)直线l和 ⊙O相交〈==〉有两个公共点;
(2)直线l和 ⊙O相切〈==〉一个公共点;
(3)直线l和 ⊙O相离〈==〉没有公共点。
如果⊙O的半径为 r,圆心O到直线 l的距离为d,
(1)直线 l 和 ⊙O相交〈==〉d < r;
(2)直线 l 和 ⊙O相切〈==〉d = r;
(3)直线 l 和 ⊙O相离〈==〉d > r。
联立直线l 与圆O的方程,
(1)如果有两组实数解,直线与圆相交;
(2)如果有一组实数解,直线与圆相切;
(3)如果没有实数解,直线与相离。
已知圆的方程是 ,直线方程 当b取何值时,直线与圆相交;相切;相离。
解法1:
根据题意得:
当直线与圆相切时,直线与圆有一个交点。
当直线与圆相离时,直线与圆有没有交点。
当直线与圆相交时,直线与圆有两个交点。
解法2:
圆心O到直线y=x+b的距离d为
当直线与圆相交时,d < r
当直线与圆相切时,d = r
当直线与圆相离时,d > r
已知点P(5,0)和⊙O:x2+y2=16
(1)自P作⊙O的切线,求切线的长及切线的方程;
(2)过P任意作直线l与⊙O交于A、B两相异点,求弦AB中点M的轨迹。
解:(1)设过P的圆O的切线切圆于点Q,
∵△PQO是直角三角形 ,
∴切线长PQ=
连OQ,
Q
(2)设M(x,y)是所求轨迹上任一点,A(x1,y1),B(x2,y2)
AB的斜率为k,
1
Δ= 0
1根
d = r
2
Δ> 0
2根
d < r
0
Δ< 0
无根
d > r
示意图形 交点个数 方程组消元后 圆心到直线d与r关系
相切
相交
相离
1.(2009 重庆)直线 与圆
的位置关系是( )
A.相切 B.相交但直线不过圆心C.直线过圆心 D.相离
B
【解析】圆心(0,0)到直线 的距
离 ,而
2.(2007 安徽)若圆
的圆心到直线 的距离为
则a的值为( )
-2或2 B. 或 C. 2或0 D. -2或0
C
【解析】易知圆心是(1,2),由
可解得a=2或0
1.对任意实数k,圆C: x2+y2-6x-8y+12=0与直线L:kx-y-4k+3=0的位置关系是( )
A 相交 B相切 C相离 D与k值有关
A
2.若直线ax+by=1与圆x2+y2=1相交,则点P(a,b)与圆的位置关系是( )
A. 在圆上 B. 在圆内
C. 在圆外 D. 以上皆有可能
C
3.若圆x2+y2=1与直线 (a>0,b>0)相切,
则ab的最小值为( )
C
4.如图,已知直线l:3x+y-6和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系;如果相交,求它们的交点坐标。
由直线l与圆的方程,得:
消去y,得:
因为:
= 1 > 0
所以,直线 l 与圆相交,有两个公共点。
所以,直线 l 与圆有两个交点,它们的坐标分别是:
A(2,0),B(1,3)
1.解:以台风中心为原点O,东西方向为x轴,建立直角坐标系,其中,取10km为单位长度。
这样,受台风影响的圆形区域所对应的圆O方程为
轮船航线AB所在直线l的方程为
4x+7y-28=0
问题归结为圆O与直线l有无公共点。
点O到直线l的距离
圆O的半径长r=3。
因为3.5>3,所以这艘轮船不必改变航线,不会受到台风的影响。
2.解:因为原点O到直线4x+3y-35=0的距离
圆心在原点,与直线4x+3y-35=0相切的圆C方程是
圆心坐标是(1,0),半径长r=1。
圆心到直线3x+4y+2=0的距离
所以直线l与圆C无公共点。
