人教版高中数学选修2-3《随机变量及其分布》导学案(学生版)
文档属性
| 名称 | 人教版高中数学选修2-3《随机变量及其分布》导学案(学生版) |  | |
| 格式 | zip | ||
| 文件大小 | 550.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 15:34:43 | ||
图片预览




文档简介
2.1.1离散型随机变量
【学习目标】理解随机变量的意义;
【自学导航】
定义1:随着试验结果变化而变化的变量称为______________
随机变量常用字母_____________… 表示.
定义2:所有取值可以一一列出的随机变量,称为_______________
判断:1。电灯的寿命X是离散型随机变量。
2.如某林场树木最高达30米,则林场树木的高度是离散型随机变量。
3.投掷一枚硬币,X=0,表示正面向上,X=1,表示反面向上X是离散型随机变量。
【合作探究】
探究1. 写出下列随机变量可能取的值
(1)一袋中装有5只同样大小的白球,编号为1,2,3,4,5 现从该袋内随机取出1只球,被取出的球的数X;
(2)某单位的某部电话在单位时间内收到的呼叫次数Y
探究2. 抛掷两枚骰子各一次,记第一枚骰子掷出的点数与第二枚骰子掷出的点数的差为X,写出X,并试问:“X> 4”表示的试验结果是什么?
探究3。一批产品共100件,其中有5件次品。现在从中认取10件检查,求取出的次品数X。
2.?1.2离散型随机变量的分布列
【学习目标】会求出某些简单的离散型随机变量的概率分布。
【自学导航】
1. 分布列:设离散型随机变量X可能取得值为
x1,x2,…,x3,…,
X取每一个值xi(i=1,2,…)的概率为,则称表
X
P
为随机变量X的概率分布,简称X的分布列
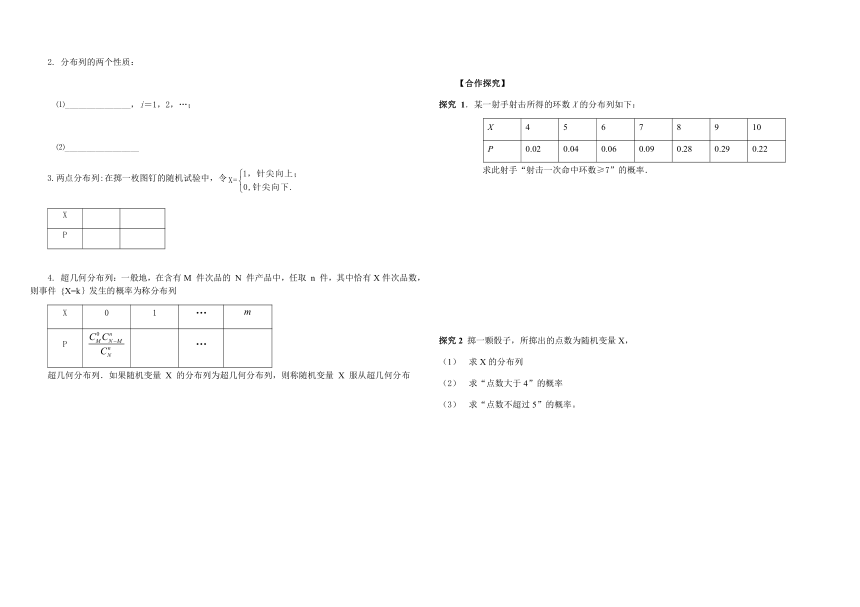
2. 分布列的两个性质:
⑴_______________,i=1,2,…;
⑵_________________
3.两点分布列:在掷一枚图钉的随机试验中,令
X
P
4. 超几何分布列:一般地,在含有M 件次品的 N 件产品中,任取 n 件,其中恰有X件次品数,则事件 {X=k}发生的概率为称分布列
X 0 1 …
P …
超几何分布列.如果随机变量 X 的分布列为超几何分布列,则称随机变量 X 服从超几何分布
【合作探究】
探究 1.某一射手射击所得的环数X的分布列如下:
X 4 5 6 7 8 9 10
P 0.02 0.04 0.06 0.09 0.28 0.29 0.22
求此射手“射击一次命中环数≥7”的概率.
探究2 掷一颗骰子,所掷出的点数为随机变量X,
(1) 求X的分布列
(2) 求“点数大于4”的概率
(3) 求“点数不超过5”的概率。
探究3在含有 5 件次品的 100 件产品中,任取 3 件,试求:
(1)取到的次品数X 的分布列;
(2)至少取到1件次品的概率.
探究4.一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球个数的一半.现从该盒中随机取出一个球,若取出红球得1分,取出黄球得0分,取出绿球得-1分,试写出从该盒中取出一球所得分数X的分布列.
【反馈练习】
在某年级的联欢会上设计了一个摸奖游戏,在一个口袋中装有10个红球和20个白球,这些球除颜色外完全相同.一次从中摸出5个球,至少摸到3个红球就中奖.
(1)求中奖的概率.
(2)如果要将这个游戏的中奖率控制在55%左右,那么应该如何设计中奖规则?
【重点归纳】
⑴根据随机变量的概率分步(分步列),可以求随机事件的概率;⑵两点分布是一种常见的离散型随机变量的分布,它是概率论中最重要的几种分布之一 (3) 离散型随机变量的超几何分布
【作业】
2.?2.1条件概率
【学习目标】通过对具体情景的分析,了解条件概率的定义。
【自学导航】
1. 定义 条件概率
2. 条件概率公式:______________.
【合作探究】
探究1.在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2 道题,求:
(l)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第 1 次抽到理科题的条件下,第2次抽到理科题的概率.
探究2.一张储蓄卡的密码共位数字,每位数字都可从0~9中任选一个.某人在银行自动提款机上取钱时,忘记了密码的最后一位数字,求:
(1)任意按最后一位数字,不超过 2 次就按对的概率;
(2)如果他记得密码的最后一位是偶数,不超过2次就按对的概率.
探究3.一个正方形被平均分成9个部分,向大正方形区域随机地投掷一个点(每次都能投中),设投中最左侧3个小正方形区域的事件记为A,投中最上面3个小正方形或正中间的1个小正方形区域的事件记为B,求P(AB),P(A︱B)。
【反馈练习】
1.抛掷一颗质地均匀的骰子所得的样本空间为S={1,2,3,4,5,6},令事件A={2,3,5},B={1,2,4,5,6},求P(A),P(B),P(AB),P(A︱B)。
2.在一个盒子中有大小一样的20个球,其中10和红球,10个白球。求第1个人摸出1个红球,紧接着第2个人摸出1个白球的概率。
3.书49页例题1-3
2.2.2事件的相互独立性
【学习目标】理解两个事件相互独立的概念。
【自学导航】
1. 相互独立事件的定义:
2. 相互独立事件性质:若与是相互独立事件,则______,________,_________也相互独立
3。一般地,如果事件相互独立,那么这个事件同时发生的概率,等于每个事件发生的概率的积,即 .
【合作探究】
探究 1.某商场推出二次开奖活动,凡购买一定价值的商品可以获得一张奖券.奖券上有一个兑奖号码,可以分别参加两次抽奖方式相同的兑奖活动.如果两次兑奖活动的中奖概率都是 0 . 05 ,求两次抽奖中以下事件的概率:
(1)都抽到某一指定号码; (2)恰有一次抽到某一指定号码; (3)至少有一次抽到某一指定号码.
探究2.甲、乙二射击运动员分别对一目标射击次,甲射中的概率为,乙射中的概率为,求:
(1)人都射中目标的概率;(2)人中恰有人射中目标的概率;
(3)人至少有人射中目标的概率;(4)人至多有人射中目标的概率?
探究 3.在一段线路中并联着3个自动控制的常开开关,只要其中有1个开关能够闭合,线路就能正常工作假定在某段时间内每个开关能够闭合的概率都是0.7,计算在这段时间内线路正常工作的概率
变式题1:如图添加第四个开关与其它三个开关串联,在某段时间内此开关能够闭合的概率也是0.7,计算在这段时间内线路正常工作的概率
变式题2:如图两个开关串联再与第三个开关并联,在某段时间内每个开关能够闭合的概率都是0.7,计算在这段时间内线路正常工作的概率
探究 4.已知某种高炮在它控制的区域内击中敌机的概率为0.2.
(1)假定有5门这种高炮控制某个区域,求敌机进入这个区域后未被击中的概率;
(2)要使敌机一旦进入这个区域后有0.9以上的概率被击中,需至少布置几门高炮?
【反馈练习】
1.在一段时间内,甲去某地的概率是,乙去此地的概率是,假定两人的行动相互之间没有影响,那么在这段时间内至少有1人去此地的概率是( )
2.从甲口袋内摸出1个白球的概率是,从乙口袋内摸出1个白球的概率是,从两个口袋内各摸出1个球,那么等于( )2个球都是白球的概率 2个球都不是白球的概率
2个球不都是白球的概率 2个球中恰好有1个是白球的概率
3.电灯泡使用时间在1000小时以上概率为0.2,则3个灯泡在使用1000小时后坏了1个的概率是( )0.128 0.096 0.104 0.384
4.某道路的、、三处设有交通灯,这三盏灯在一分钟内开放绿灯的时间分别为25秒、35秒、45秒,某辆车在这条路上行驶时,三处都不停车的概率是 ( )
5.(1)将一个硬币连掷5次,5次都出现正面的概率是 ;
(2)甲、乙两个气象台同时作天气预报,如果它们预报准确的概率分别是0.8与0.7,那么在一次预报中两个气象台都预报准确的概率是 .
6.棉籽的发芽率为0.9,发育为壮苗的概率为0.6,
(1)每穴播两粒,此穴缺苗的概率为 ;此穴无壮苗的概率为 .
(2)每穴播三粒,此穴有苗的概率为 ;此穴有壮苗的概率为 .
7.一个工人负责看管4台机床,如果在1小时内这些机床不需要人去照顾的概率第1台是0.79,第2台是0.79,第3台是0.80,第4台是0.81,且各台机床是否需要照顾相互之间没有影响,计算在这个小时内这4台机床都不需要人去照顾的概率.
8.制造一种零件,甲机床的废品率是0.04,乙机床的废品率是0.05.从它们制造的产品中各任抽1件,其中恰有1件废品的概率是多少?
2.2.3独立重复实验与二项分布
【学习目标】理解n次独立重复试验的模型及二项分布,并能解答一些简单的实际问题。
【自学导航】
二、讲解新课:
1XXX独立重复试验的定义:
2.独立重复试验的概率公式: ________________________________.
3.离散型随机变量的二项分布: ,(k=0,1,2,…,n,).
于是得到随机变量X的概率分布如下:
X 0 1 … k … n
P … …
这样的随机变量X服从二项分布,记作X~B(n,p)
【合作探究】
探究1.某射手每次射击击中目标的概率是0 . 8.求这名射手在 10 次射击中,
(1)恰有 8 次击中目标的概率;
(2)至少有 8 次击中目标的概率.(结果保留两个有效数字.)
探究2.(2000年高考题)某厂生产电子元件,其产品的次品率为5%.现从一批产品中任意地连续取出2件,写出其中次品数X的概率分布.
探究3.重复抛掷一枚筛子5次得到点数为6的次数记为X,求P(X>3).
探究4.某气象站天气预报的准确率为,计算(结果保留两个有效数字):
(1)5次预报中恰有4次准确的概率;
(2)5次预报中至少有4次准确的概率
探究5.某车间的5台机床在1小时内需要工人照管的概率都是,求1小时内5台机床中至少2台需要工人照管的概率是多少?(结果保留两个有效数字)
探究6.某人对一目标进行射击,每次命中率都是0.25,若使至少命中1次的概率不小于0.75,至少应射击几次?
探究7.十层电梯从低层到顶层停不少于3次的概率是多少?停几次概率最大?
探究8.实力相等的甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛).
(1)试分别求甲打完3局、4局、5局才能取胜的概率.
(2)按比赛规则甲获胜的概率.
【反馈练习】
1.每次试验的成功率为,重复进行10次试验,其中前7次都未成功后3次都成功的概率为( )
2.10张奖券中含有3张中奖的奖券,每人购买1张,则前3个购买者中,恰有一人中奖的概率为( )
3.甲、乙两队参加乒乓球团体比赛,甲队与乙队实力之比为,比赛时均能正常发挥技术水平,则在5局3胜制中,甲打完4局才胜的概率为( )
4.一射手命中10环的概率为0.7,命中9环的概率为0.3,则该射手打3发得到不少于29环的概率为 .(设每次命中的环数都是自然数)
5.一名篮球运动员投篮命中率为,在一次决赛中投10个球,则投中的球数不少于9个的概率为 .
2.3.1离散型随机变量的期望
【学习目标】
了解离散型随机变量的均值或期望的意义,会根据离散型随机变量的分布列求出均值或期望.
【自学导航】
1. 均值或数学期望: 一般地,若离散型随机变量X的概率分布为
X x1 x2 … xn …
P p1 p2 … pn …
则称 _______________________________________________为X的均值或数学期望,简称期望.
2. 均值或数学期望意义:是离散型随机变量的一个特征数,它反映了离散型随机变量取值的______
3. 性质:
4.若X~B(n,p),则np.
【合作探究】
探究1. 篮球运动员在比赛中每次罚球命中得1分,罚不中得0分,已知他命中的概率为0.7,求他罚球一次得分X的期望
探究2. 一次单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分 学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望
探究3.随机抛掷一枚骰子,求所得骰子点数X的期望
探究4.袋中有4个黑球、3个白球、2个红球,从中任取2个球,每取到一个黑球记0分,每取到一个白球记1分,每取到一个红球记2分,用X表示得分数
x的概率分布列.2.求X的数学期望
(拔高)探究5.某城市出租汽车的起步价为10元,行驶路程不超出4km时租车费为10元,若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足lkm的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机经常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程X是一个随机变量.设他所收租车费为Y
(Ⅰ)求租车费Y关于行车路程X的关系式;
(Ⅱ)若随机变量X的分布列为
X 15 16 17 18
P 0.1 0.5 0.3 0.1
求所收租车费Y的数学期望.
(Ⅲ)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟?
【反馈练习:
1.口袋中有5只球,编号为1,2,3,4,5,从中任取3球,以表示取出球的最大号码,则( )
A.4; B.5; C.4.5; D.4.75
2. 篮球运动员在比赛中每次罚球命中的1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,求⑴他罚球1次的得分X的数学期望;⑵他罚球2次的得分Y的数学期望;
⑶他罚球3次的得分X的数学期望.
3.设有m升水,其中含有大肠杆菌n个.今取水1升进行化验,设其中含有大肠杆菌的个数为X,求X的数学期望.
【重点归纳】 (1)离散型随机变量的期望,反映了随机变量取值的平均水平;
(2)求离散型随机变量X的期望的基本步骤:①理解X的意义,写出X可能取的全部值;②求X取各个值的概率,写出分布列;③根据分布列,由期望的定义求出EX 公式E(aX+b)= aEX+b,以及服从二项分布的随机变量的期望EX=np
【重点归纳】【作业】
2.3.2离散型随机变量的方差
【学习目标】
解离散型随机变量的方差、标准差的意义,会根据离散型随机变量的分布列求出方差或标准差。
【自学导航】
1. 方差:
2. 标准差:
3.方差的性质:(1);(2);
(3)若X~B(n,p),则np(1-p)
4.方差意义:
随机变量X的方差、标准差也是随机变量X的特征数,它们都反映了随机变量取值的稳定与波动、集中与离散的程度;标准差与随机变量本身有相同的单位,所以在实际问题中应用更广泛
【合作探究】
探究1.随机抛掷一枚质地均匀的骰子,求向上一面的点数的均值、方差和标准差.
探究2.有甲乙两个单位都愿意聘用你,而你能获得如下信息:
甲单位不同职位月工资X1/元 1200 1400 1600 1800
获得相应职位的概率P1 0.4 0.3 0.2 0.1
乙单位不同职位月工资X2/元 1000 1400 1800 2000
获得相应职位的概率P2 0.4 0.3 0.2 0.1
根据工资待遇的差异情况,你愿意选择哪家单位?
探究3.设随机变量X的分布列为
X 1 2 … n
P …
求DX
探究4.已知离散型随机变量的概率分布为
1 2 3 4 5 6 7
P
离散型随机变量的概率分布为
3.7 3.8 3.9 4 4.1 4.2 4.3
P
求这两个随机变量期望、均方差与标准差
探究5.甲、乙两射手在同一条件下进行射击,分布列如下:射手甲击中环数8,9,10的概率分别为0.2,0.6,0.2;射手乙击中环数8,9,10的概率分别为0.4,0.2,0.24用击中环数的期望与方差比较两名射手的射击水平
【反馈练习】
1 .已知,则的值分别是( )
A.; B.; C.; D.
2. 一盒中装有零件12个,其中有9个正品,3个次品,从中任取一个,如果每次取出次品就不再放回去,再取一个零件,直到取得正品为止.求在取得正品之前已取出次品数的期望.
3. 有A、B两种钢筋,从中取等量样品检查它们的抗拉强度,指标如下:
XA 110 120 125 130 135 XB 100 115 125 130 145
P 0.1 0.2 0.4 0.1 0.2 P 0.1 0.2 0.4 0.1 0.2
其中XA、XB分别表示A、B两种钢筋的抗拉强度.在使用时要求钢筋的抗拉强度不低于120,试比较A、B两种钢筋哪一种质量较好
【重点归纳】
【作业】
2.4正态分布
【学习目标】掌握正态分布在实际生活中的意义和作用 。
【自学导航】
1.总体密度曲线:
2.正态曲线:图象来表示或近似表示: 式中的实数、是参数,分别表示总体的平均数与标准差,的图象为正态分布密度曲线.
3.X 的分布为正态分布:
一般地,如果对于任何实数,随机变量X满足
,.正态分布完全由参数和确定,记为X~.
4.正态曲线的性质:
(1)曲线在x轴的上方,与x轴不相交 (2)曲线关于直线x=μ对称
(3)当x=μ时,曲线位于最高点
(4)当x<μ时,曲线上升(增函数);当x>μ时,曲线下降(减函数) 并且当曲线向左、右两边无限延伸时,以x轴为渐近线,向它无限靠近
(5)μ一定时,曲线的形状由σ确定 σ越大,曲线越“矮胖”,总体分布越分散;σ越小.曲线越“瘦高”.总体分布越集中:
5.标准正态曲线:当μ=0、σ=l时,正态总体称为标准正态总体,其相应的函数表示式,(-∞<x<+∞)其相应的曲线称为标准正态曲线
【合作探究】
探究1.给出下列三个正态总体的函数表达式,请找出其均值μ和标准差σ
(1)
(2)
(3)
探究2. 若x~N(0,1),求(l)P(-2.32
探究3.利用标准正态分布表,求标准正态总体在下面区间取值的概率:
(1)在N(1,4)下,求
(2)在N(μ,σ2)下,求F(μ-σ,μ+σ);
探究4.某正态总体函数的概率密度函数是偶函数,而且该函数的最大值为,求总体落入区间(-1.2,0.2)之间的概率
第二章 条件概率的知识点
1.随机变量:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量 随机变量常用希腊字母X、Y等表示
2. 离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量
3. 分布列:
X x1 x2 … xi …
P P1 P2 … Pi …
4. 分布列的两个性质: ⑴Pi≥0,i=1,2,…; ⑵P1+P2+…=1.
5.二项分布:X~B(n,p),并记=b(k;n,p).
X 0 1 … k … n
P … …
6.几何分布: g(k,p)= ,其中k=0,1,2,…, .
X 1 2 3 … k …
P … …
7.数学期望: 一般地,若离散型随机变量X的概率分布为
X x1 x2 … xn …
P p1 p2 … pn …
则称 …… 为X的数学期望,简称期望.
8. 数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平
9 平均数、均值:在有限取值离散型随机变量X的概率分布中,令…,则有…,…,所以X的数学期望又称为平均数、均值
10. 期望的一个性质:
11.若XB(n,p),则EX=np
12.=++…++…
称为随机变量ξ的均方差,简称为方差,式中的是随机变量ξ的期望.
13.(1);(2);
(3)若ξ~B(n,p),则np(1-p)
14.标准正态曲线:当μ=0、σ=l时,正态总体称为标准正态总体,其相应的函数表示式是,(-∞<x<+∞)
15.标准正态分布表中对应于的值是指总体取值小于的概率,即 ,.若,则.
利用标准正态分布表,可以求出标准正态总体在任意区间内取值的概率,即直线,与正态曲线、x轴所围成的曲边梯形的面积.
