4.2.2圆与圆的位置关系(共29张PPT)
文档属性
| 名称 | 4.2.2圆与圆的位置关系(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 898.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 00:00:00 | ||
图片预览



文档简介
(共29张PPT)
4.2.2 圆与圆的位置关系
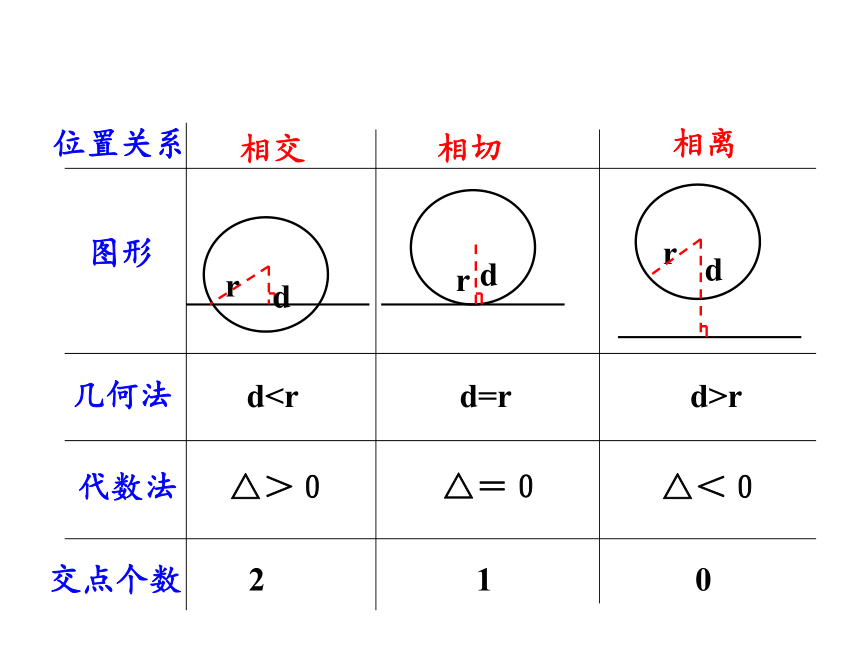
直线与圆的位置关系的判定
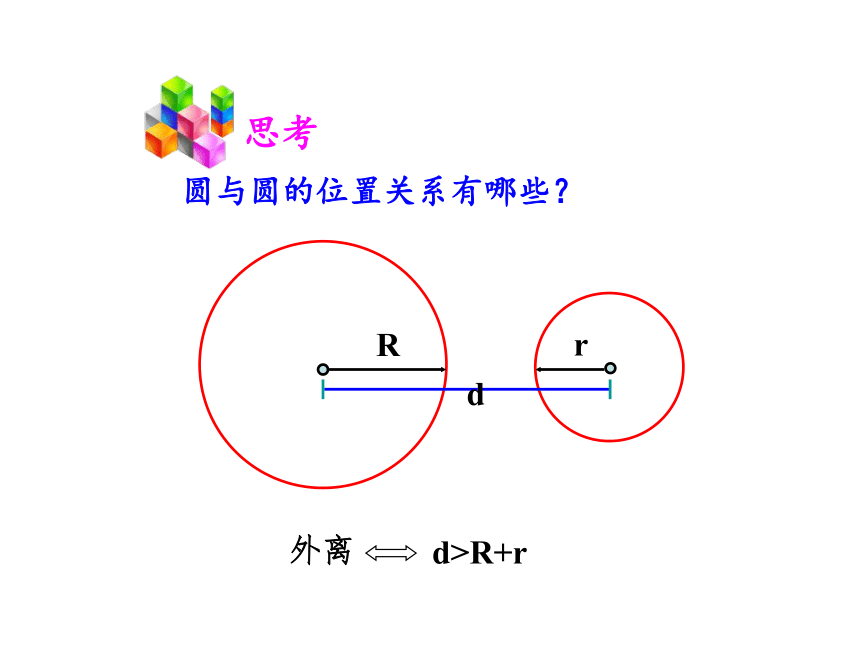
圆与圆的位置关系有哪些?
随着连心距的增加,两圆的关系发生变化。
已知两圆C1:x2+y2+D1x+E1y+F1=0和C2:x2+y2+D2x+E2y+F2=0,如何根据圆的方程判断圆与圆的位置关系?
1.将两圆的方程化为标准方程;
2.求两圆的圆心坐标和半径R、r;
3.求两圆的圆心距d;
4.比较d与R-r,R+r的大小关系.
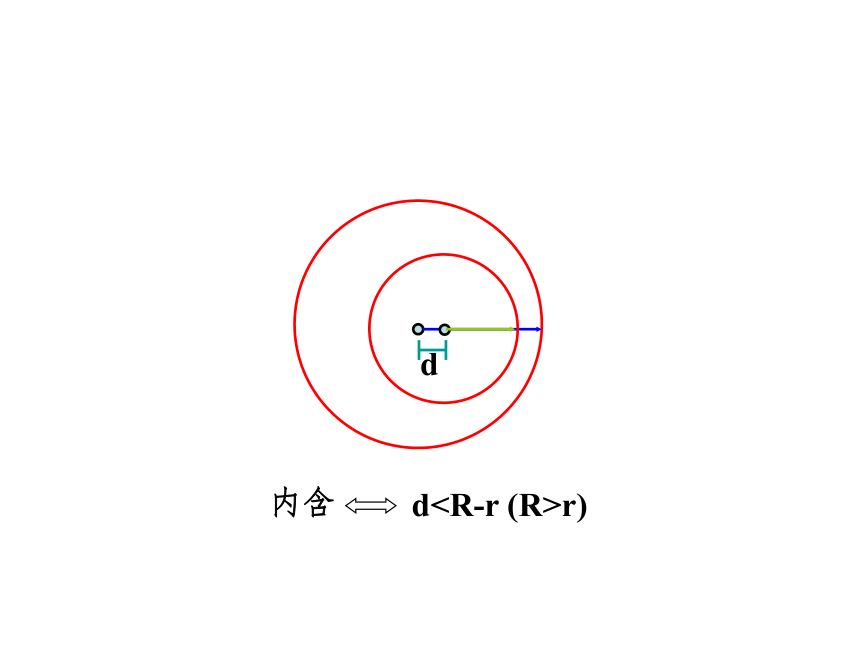
若d<|R-r|,则两圆内含;
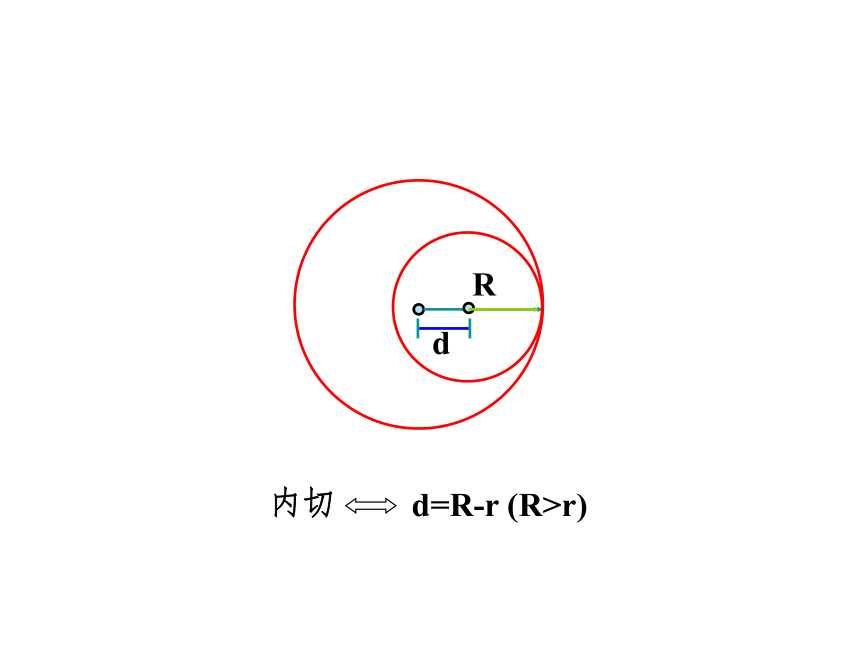
若d=|R-r|,则两圆内切;
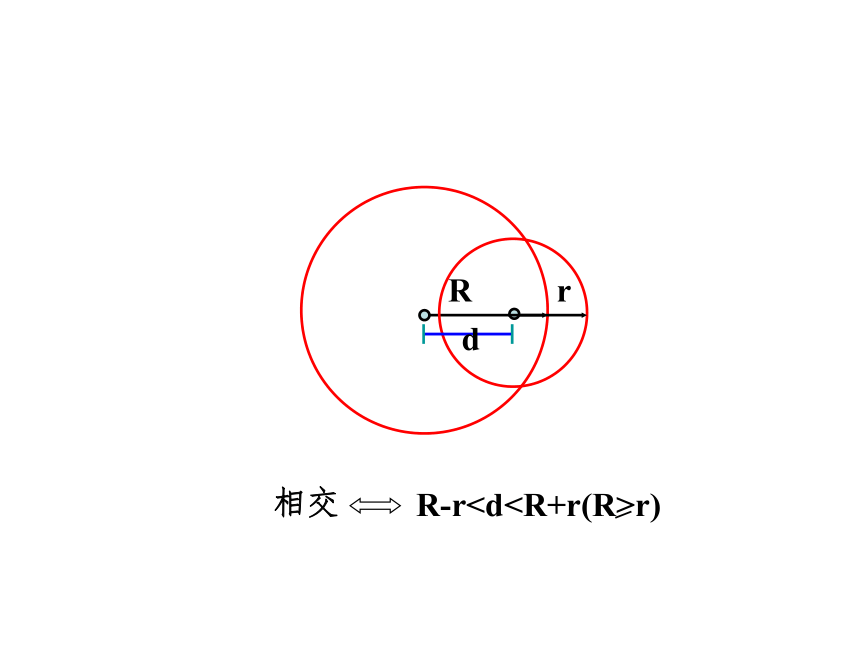
若|R-r|<d<R+r,则两圆相交;
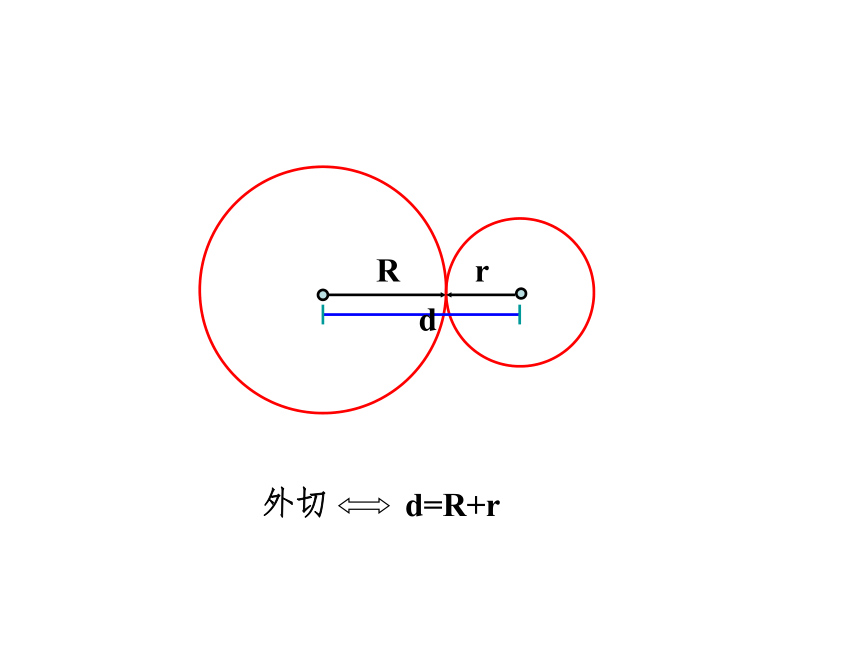
若d=R+r,则两圆外切;
若d>R+r,则两圆外离。
能否根据两个圆的公共点个数判断两圆的位置关系?
利用两个圆的方程组成方程组的实数解的个数:
已知圆C1:x2+y2-6x+8y=0和圆C2:x2+y2+2x-3=0,试判断圆C1与圆C2的位置关系。
将C1的方程化成标准方程,得
将C2的方程化成标准方程,得
圆心坐标(3,-4),半径为5。
圆心坐标(-1,0),半径为2。
圆C1与C2的连心线的长为:
圆C1与圆C2的半径长之和为:
r1+r2=5+2=7
圆C1与圆C2的半径长之差为:
r1-r2=5-2=3
所以两圆相交。
判断两圆的位置关系的两种方法:
1.根据圆心距与半径和之间的大小关系。
若d<|R-r|,则两圆内含;
若d=|R-r|,则两圆内切;
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离。
2.联立两圆方程,看截得解得个数.
【解析】由题意,得
,故选B
B
1.判断下列两圆的位置关系。
(2)圆A:x2+y2=1与圆B:x2+y2+6x-8y-24=0的位置关系是___________
内切
2 .已知两圆(x-3)2 + (y-2)2=25和(x-1)2+ (y-2)2=r2相内切,则半径r= ( )
B
(1)圆A:(x-3)2+(y+2)2=1与圆B:(x-7)2+(y-1)2=36的位置关系是___________
内含
3.两圆半径是方程 2x2-10x+3=0 的两个实数根 ,当两圆的圆心距等于 7 时,它们的位置关系是( )
A. 相交 B. 外切 C. 内切 D. 外离
4.两圆半径之比为 1 : 2 ,已知这两个圆内切时的圆心距为5,那么这两圆相交时圆心距 d 的取值范围为( )
A.d>5 B.5C.515
D
B
外离
0
6.两个同心圆的位置关系是:_______。
内含
7.圆O1和圆O2的半径分别为R、r,圆心距为d,下列情况下圆O1和圆O2的位置关系怎样?
(1)R=4 r=3 d=8
外离
(2)R=4 r=3 d=1
内切
(3)R=1 r=6 d=7
外切
(4)R=5 r=3 d=3
相交
(5)R=5 r=3 d=1
内含
5.把自行车的两个轮子看作两个圆,则它们的位置关系_______公共点______个。
8.两圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径为_______。
3或7
9.已知⊙O1、⊙O2的半径为r1、r2,如果r1=5,r2=3,且⊙O1、⊙O2相切,那么圆心距d=________。
8或2
C1 (-1,-4)
C2(2,2)
交点坐标A(-1,1),B(3,1)
直线方程为
x+2y-1=0
解:联立方程组,得
x
y
A
B
分析:R + r = 15,R – r = 5
所以:R=10,r=5。
C
解法一:
将C1的方程化成标准方程,得
将C2的方程化成标准方程,得
圆C1与C2的连心线的长为:
圆C1与圆C2的半径长之和为:
圆C1与圆C2的半径长之差为:
所以两圆相交。
解法二:
4.2.2 圆与圆的位置关系
直线与圆的位置关系的判定
圆与圆的位置关系有哪些?
随着连心距的增加,两圆的关系发生变化。
已知两圆C1:x2+y2+D1x+E1y+F1=0和C2:x2+y2+D2x+E2y+F2=0,如何根据圆的方程判断圆与圆的位置关系?
1.将两圆的方程化为标准方程;
2.求两圆的圆心坐标和半径R、r;
3.求两圆的圆心距d;
4.比较d与R-r,R+r的大小关系.
若d<|R-r|,则两圆内含;
若d=|R-r|,则两圆内切;
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离。
能否根据两个圆的公共点个数判断两圆的位置关系?
利用两个圆的方程组成方程组的实数解的个数:
已知圆C1:x2+y2-6x+8y=0和圆C2:x2+y2+2x-3=0,试判断圆C1与圆C2的位置关系。
将C1的方程化成标准方程,得
将C2的方程化成标准方程,得
圆心坐标(3,-4),半径为5。
圆心坐标(-1,0),半径为2。
圆C1与C2的连心线的长为:
圆C1与圆C2的半径长之和为:
r1+r2=5+2=7
圆C1与圆C2的半径长之差为:
r1-r2=5-2=3
所以两圆相交。
判断两圆的位置关系的两种方法:
1.根据圆心距与半径和之间的大小关系。
若d<|R-r|,则两圆内含;
若d=|R-r|,则两圆内切;
若|R-r|<d<R+r,则两圆相交;
若d=R+r,则两圆外切;
若d>R+r,则两圆外离。
2.联立两圆方程,看截得解得个数.
【解析】由题意,得
,故选B
B
1.判断下列两圆的位置关系。
(2)圆A:x2+y2=1与圆B:x2+y2+6x-8y-24=0的位置关系是___________
内切
2 .已知两圆(x-3)2 + (y-2)2=25和(x-1)2+ (y-2)2=r2相内切,则半径r= ( )
B
(1)圆A:(x-3)2+(y+2)2=1与圆B:(x-7)2+(y-1)2=36的位置关系是___________
内含
3.两圆半径是方程 2x2-10x+3=0 的两个实数根 ,当两圆的圆心距等于 7 时,它们的位置关系是( )
A. 相交 B. 外切 C. 内切 D. 外离
4.两圆半径之比为 1 : 2 ,已知这两个圆内切时的圆心距为5,那么这两圆相交时圆心距 d 的取值范围为( )
A.d>5 B.5
D
B
外离
0
6.两个同心圆的位置关系是:_______。
内含
7.圆O1和圆O2的半径分别为R、r,圆心距为d,下列情况下圆O1和圆O2的位置关系怎样?
(1)R=4 r=3 d=8
外离
(2)R=4 r=3 d=1
内切
(3)R=1 r=6 d=7
外切
(4)R=5 r=3 d=3
相交
(5)R=5 r=3 d=1
内含
5.把自行车的两个轮子看作两个圆,则它们的位置关系_______公共点______个。
8.两圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径为_______。
3或7
9.已知⊙O1、⊙O2的半径为r1、r2,如果r1=5,r2=3,且⊙O1、⊙O2相切,那么圆心距d=________。
8或2
C1 (-1,-4)
C2(2,2)
交点坐标A(-1,1),B(3,1)
直线方程为
x+2y-1=0
解:联立方程组,得
x
y
A
B
分析:R + r = 15,R – r = 5
所以:R=10,r=5。
C
解法一:
将C1的方程化成标准方程,得
将C2的方程化成标准方程,得
圆C1与C2的连心线的长为:
圆C1与圆C2的半径长之和为:
圆C1与圆C2的半径长之差为:
所以两圆相交。
解法二:
