1.1.2弧度制(共41张PPT)
文档属性
| 名称 | 1.1.2弧度制(共41张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 20:14:03 | ||
图片预览









文档简介
(共41张PPT)
1.1.2 弧度制
生活中,存在着各种不同的度量单位制,比如度量长度用的千米、尺、码等,度量重量用的吨、斤、磅等,不同单位制能给解决问题带来便利,角的度量除了用度之外,是不是还有其他的单位制呢?
角的度量
角度制
弧度制
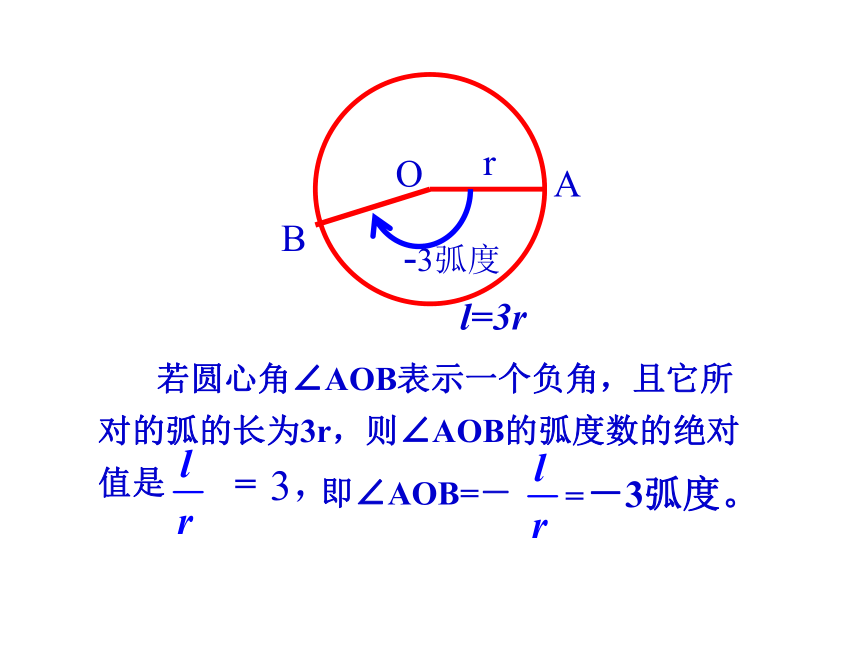
把长度等于半径长的弧所对的圆心角叫做1弧度的角。
定义:
符号:
rad
读作:弧度。
就是1弧度的角。
如图,圆O的半径是1,
的长等于1,
l
2弧度
r
-3弧度
1、弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度;
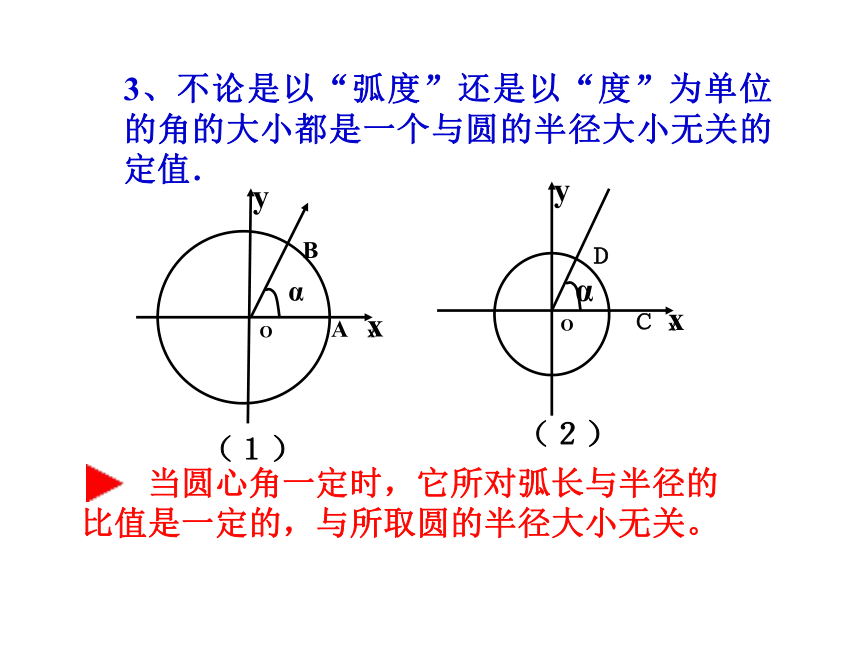
当圆心角一定时,它所对弧长与半径的比值是一定的,与所取圆的半径大小无关。
3、不论是以“弧度”还是以“度”为单位的角的大小都是一个与圆的半径大小无关的定值.
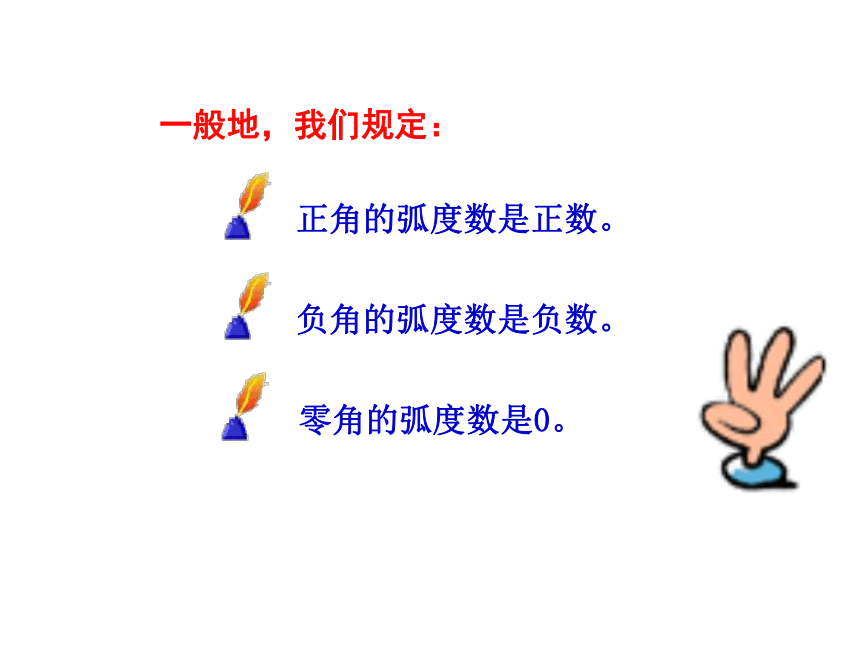
一般地,我们规定:
角?的弧度数的绝对值
弧度数的绝对值公式
如图,半径为r的圆的圆心与原点重合,角α的始边与x轴的正半轴重合,交圆与点A,终边与圆交与点B.请在下列表格中填空。
的长 OB旋转的方向 的弧度数 的度数
逆时针方向
逆时针方向
逆时针方向 1
顺时针 -2
顺时针
0 未旋转 0
逆时针方向
逆时针方向
由上表可知,如果一个半径为r的圆的圆心角α所对的弧长是l,那么α的弧度制的绝对值是
例1:已知扇形的周长是6cm,面积是2cm?,则扇形的圆心角的弧度数是( )
A.1 B.1或4
C.4 D.2或4
B
A.“度”与“弧度”是度量的两种不同的度量单位
C.根据弧度的定义,180°一定等于π弧度
D.不论是用角度制还是弧度制度量角,它们与圆的半径长短有关
例2:下列选项中,错误的是( )
D
B.一度的角是周角的 ,一弧度的角是周角的
周角的弧度数是2π,而在角度制下的度数是360。
∴
360°= 2πrad;
180°= πrad.
锐角: {θ|0°<θ<90°},
直角: {θ|θ=90°}
钝角: {θ|90°<θ<180°}
平角: {θ|θ=180°}
周角: {θ|θ=360°}
例3:请用弧度制表示下列角度的范围.
0°到90°的角:{θ|0°≤θ<90°};
小于90°角:{θ|θ<90°}
0°到180°的角:{θ|0°≤θ<180°}
0°到360°的角:{θ|0°≤θ<360°}
例4:将下列弧度转化为角度:
= °;
(3)
= °.
(1)
= ° ′;
(2)
15
-157
30
390
(1)36°= (rad);
例5:将下列角度转化为弧度:
(3)37°30′= (rad).
(2)-105°= (rad);
注:今后我们用弧度制表示角的时候,“弧度”二字或者“rad”通常省略不写,而只写这个角所对应的弧度数.但如果以度( 。)为 单位表示角时,度( 。)不能省略.
1、弧度制下角的集合与实数集的一一对应:
正角
零角
负角
正实数
零
负实数
2、求弧长:
已知扇形的周长为30cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
例8:
1、弧度制的概念
2、弧度制和角度制的比较与换算
具体总结如下表:
π =180°
1rad=
57°18′,
1°=
rad=0.01745 rad
弧度制 角度制
度量单位 弧度 角度
单位规定 等于半径的长的圆弧所对应的圆心角叫1 的角
周角的 为1度的角
换算关系
B
2、计算
3、67°30′化成弧度。
4、 把 化成度。
5、如图,已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。
解:设扇形的半径为r,弧长为l ,则有
6、已知一个扇形的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。
7、已知扇形AOB的圆心角为120°,半径为6,求此扇形所含弓形面积。
1、(1) (2) (3)
2、(1)15°(2)-240°(3)54°
3、(1)
(2)
5、
6、弧度数为1.2
4、(1)
(2)
1.1.2 弧度制
生活中,存在着各种不同的度量单位制,比如度量长度用的千米、尺、码等,度量重量用的吨、斤、磅等,不同单位制能给解决问题带来便利,角的度量除了用度之外,是不是还有其他的单位制呢?
角的度量
角度制
弧度制
把长度等于半径长的弧所对的圆心角叫做1弧度的角。
定义:
符号:
rad
读作:弧度。
就是1弧度的角。
如图,圆O的半径是1,
的长等于1,
l
2弧度
r
-3弧度
1、弧度制是以“弧度”为单位度量角的制度,角度制是以“度”为单位度量角的制度;
当圆心角一定时,它所对弧长与半径的比值是一定的,与所取圆的半径大小无关。
3、不论是以“弧度”还是以“度”为单位的角的大小都是一个与圆的半径大小无关的定值.
一般地,我们规定:
角?的弧度数的绝对值
弧度数的绝对值公式
如图,半径为r的圆的圆心与原点重合,角α的始边与x轴的正半轴重合,交圆与点A,终边与圆交与点B.请在下列表格中填空。
的长 OB旋转的方向 的弧度数 的度数
逆时针方向
逆时针方向
逆时针方向 1
顺时针 -2
顺时针
0 未旋转 0
逆时针方向
逆时针方向
由上表可知,如果一个半径为r的圆的圆心角α所对的弧长是l,那么α的弧度制的绝对值是
例1:已知扇形的周长是6cm,面积是2cm?,则扇形的圆心角的弧度数是( )
A.1 B.1或4
C.4 D.2或4
B
A.“度”与“弧度”是度量的两种不同的度量单位
C.根据弧度的定义,180°一定等于π弧度
D.不论是用角度制还是弧度制度量角,它们与圆的半径长短有关
例2:下列选项中,错误的是( )
D
B.一度的角是周角的 ,一弧度的角是周角的
周角的弧度数是2π,而在角度制下的度数是360。
∴
360°= 2πrad;
180°= πrad.
锐角: {θ|0°<θ<90°},
直角: {θ|θ=90°}
钝角: {θ|90°<θ<180°}
平角: {θ|θ=180°}
周角: {θ|θ=360°}
例3:请用弧度制表示下列角度的范围.
0°到90°的角:{θ|0°≤θ<90°};
小于90°角:{θ|θ<90°}
0°到180°的角:{θ|0°≤θ<180°}
0°到360°的角:{θ|0°≤θ<360°}
例4:将下列弧度转化为角度:
= °;
(3)
= °.
(1)
= ° ′;
(2)
15
-157
30
390
(1)36°= (rad);
例5:将下列角度转化为弧度:
(3)37°30′= (rad).
(2)-105°= (rad);
注:今后我们用弧度制表示角的时候,“弧度”二字或者“rad”通常省略不写,而只写这个角所对应的弧度数.但如果以度( 。)为 单位表示角时,度( 。)不能省略.
1、弧度制下角的集合与实数集的一一对应:
正角
零角
负角
正实数
零
负实数
2、求弧长:
已知扇形的周长为30cm,当它的半径和圆心角各取什么值时,才能使扇形的面积最大?最大面积是多少?
例8:
1、弧度制的概念
2、弧度制和角度制的比较与换算
具体总结如下表:
π =180°
1rad=
57°18′,
1°=
rad=0.01745 rad
弧度制 角度制
度量单位 弧度 角度
单位规定 等于半径的长的圆弧所对应的圆心角叫1 的角
周角的 为1度的角
换算关系
B
2、计算
3、67°30′化成弧度。
4、 把 化成度。
5、如图,已知扇形AOB的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。
解:设扇形的半径为r,弧长为l ,则有
6、已知一个扇形的周长是6cm,该扇形的中心角是1弧度,求该扇形的面积。
7、已知扇形AOB的圆心角为120°,半径为6,求此扇形所含弓形面积。
1、(1) (2) (3)
2、(1)15°(2)-240°(3)54°
3、(1)
(2)
5、
6、弧度数为1.2
4、(1)
(2)
