2.2.3向量数乘运算及其几何意义(共15张PPT)
文档属性
| 名称 | 2.2.3向量数乘运算及其几何意义(共15张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 545.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-28 20:17:48 | ||
图片预览




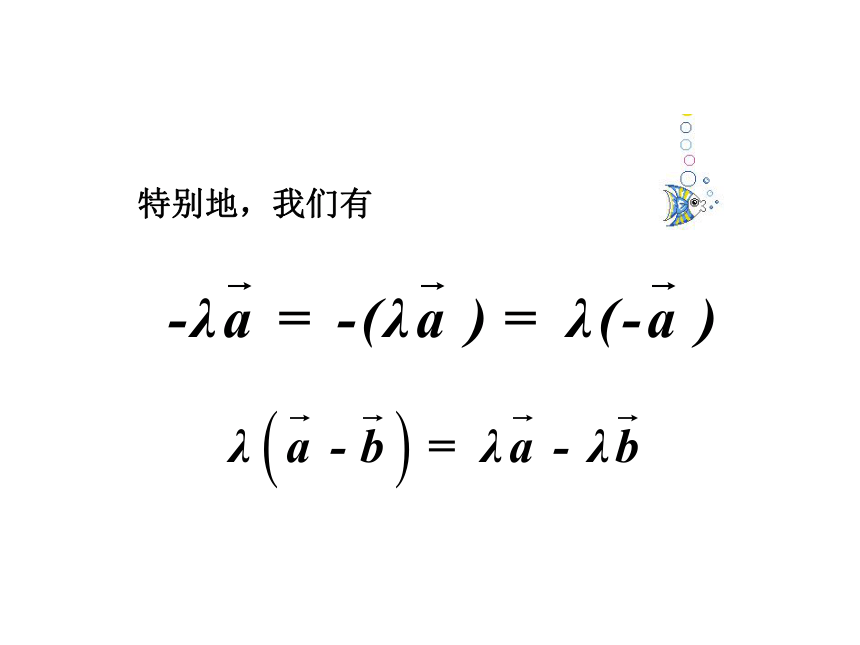

文档简介
(共15张PPT)
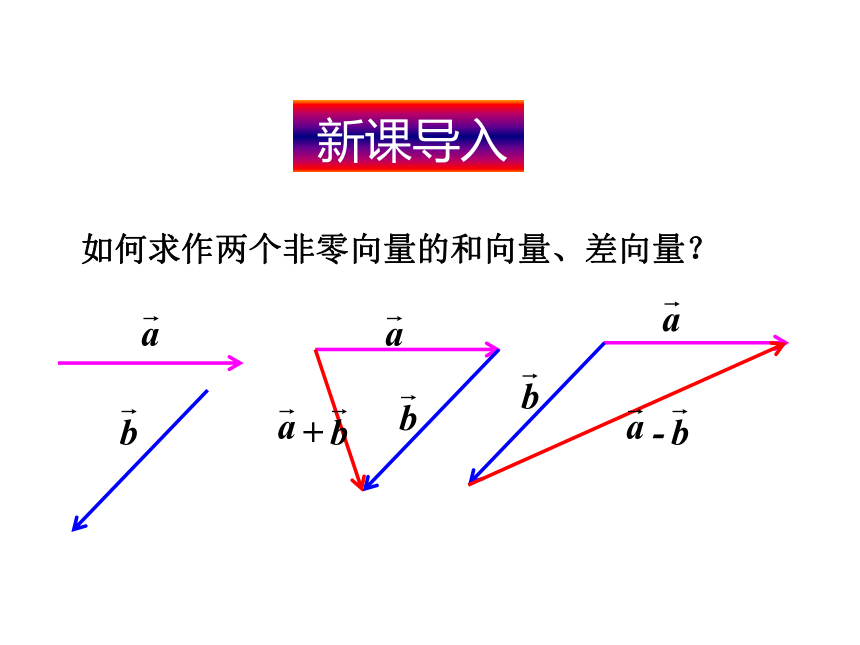
如何求作两个非零向量的和向量、差向量?
新课导入
向量的数乘的定义:
记作:
它的长度和方向规定如下:
数乘向量的运算律:
结合律
第一分配律
第二分配律
特别地,我们有
定理
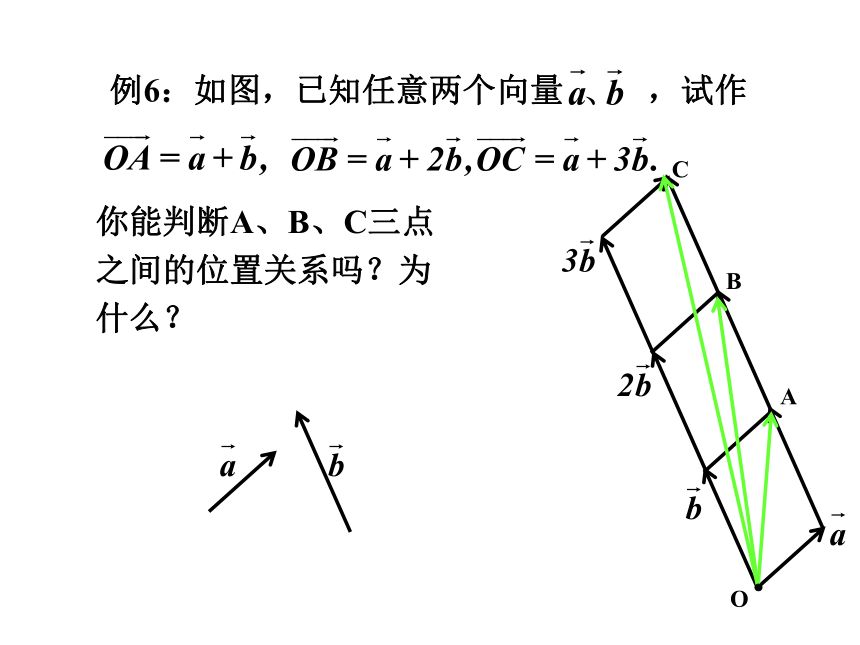
例6:如图,已知任意两个向量 ,试作
你能判断A、B、C三点之间的位置关系吗?为什么?
A
B
C
练习1、设 是两个不共线的向量,
,若A,B,D三点共线,求k的值。
解:
若A,B,D三点共线,则
共线,
,即
由于
可得:
练习2、如图,在平行四边形ABCD中,点M是AB中点,点N在线段BD上,且有 BN= BD,求证:M、N、C三点共线。
证明:
1、实数与向量可以相乘,其积仍是向量,但实数与向量不能相加、相减.实数除以向量没有意义,向量除以非零实数就是数乘向量.
3、向量的数乘运算律,不是规定,而是可以证明的结论。向量共线定理是平面几何中证明三点共线,直线平行,线段比例关系的理论依据。
coNe
如何求作两个非零向量的和向量、差向量?
新课导入
向量的数乘的定义:
记作:
它的长度和方向规定如下:
数乘向量的运算律:
结合律
第一分配律
第二分配律
特别地,我们有
定理
例6:如图,已知任意两个向量 ,试作
你能判断A、B、C三点之间的位置关系吗?为什么?
A
B
C
练习1、设 是两个不共线的向量,
,若A,B,D三点共线,求k的值。
解:
若A,B,D三点共线,则
共线,
,即
由于
可得:
练习2、如图,在平行四边形ABCD中,点M是AB中点,点N在线段BD上,且有 BN= BD,求证:M、N、C三点共线。
证明:
1、实数与向量可以相乘,其积仍是向量,但实数与向量不能相加、相减.实数除以向量没有意义,向量除以非零实数就是数乘向量.
3、向量的数乘运算律,不是规定,而是可以证明的结论。向量共线定理是平面几何中证明三点共线,直线平行,线段比例关系的理论依据。
coNe
