人教版八年级上册数学第十五章分式复习课件(18张PPT)
文档属性
| 名称 | 人教版八年级上册数学第十五章分式复习课件(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 325.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 14:57:10 | ||
图片预览






文档简介
(共21张PPT)
分式总复习
第15章分式
复习目标
1.复习分式的定义与基本性质。
2.复习约分、通分的定义和方法。
3.复习分式的运算。
复习指导
认真复习课本127页----142页的内容,注意:
1.对于掌握不太牢固的概念,性质用笔勾画出来。加强记忆。
2.对于有疑问的习题,可请教老师或同学,彻底扫除疑问。
5分钟后,我们进行检测。
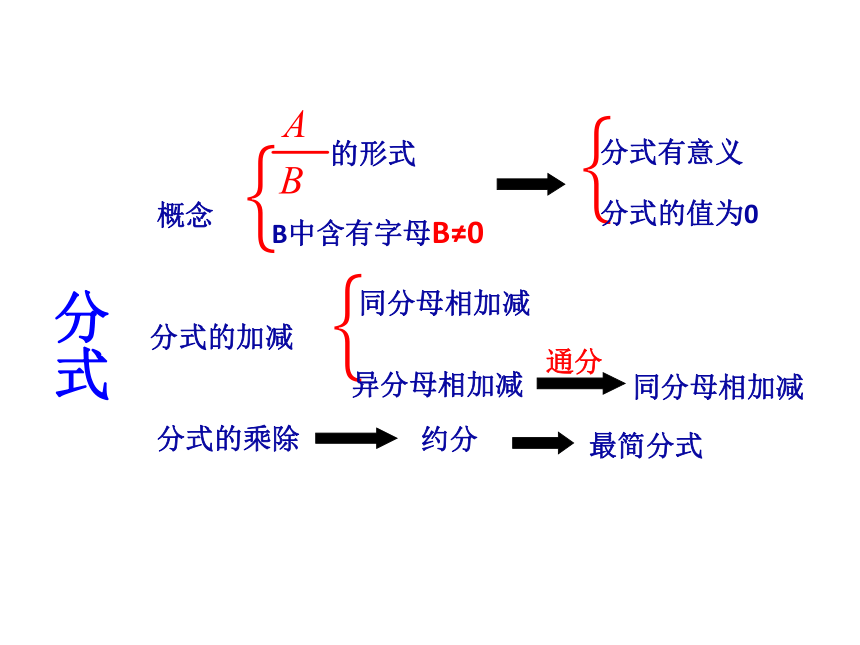
分式
分式有意义
分式的值为0
同分母相加减
异分母相加减
概念
的形式
B中含有字母B≠0
分式的加减
分式的乘除
通分
约分
最简分式
同分母相加减
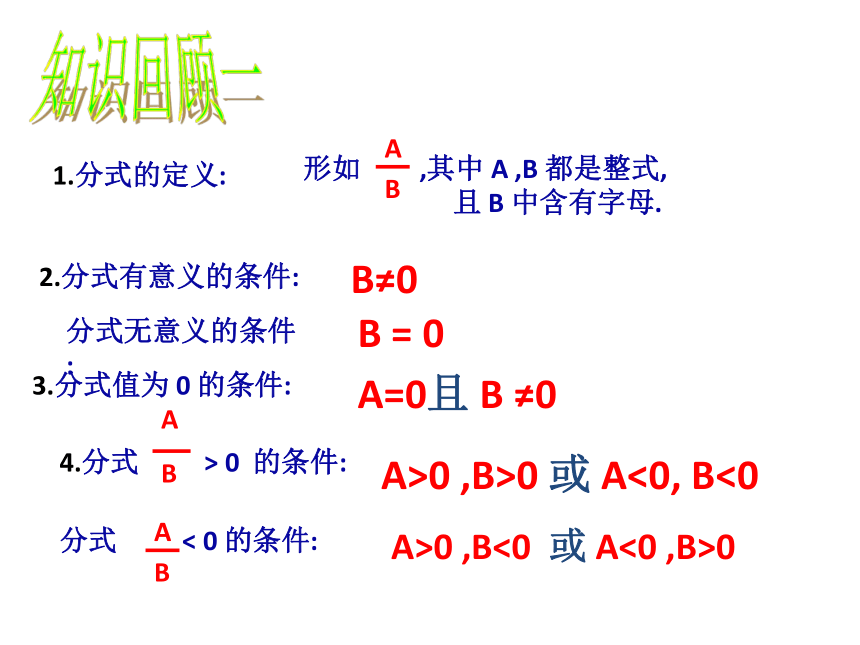
知识回顾一
1.分式的定义:
2.分式有意义的条件:
B≠0
分式无意义的条件:
B = 0
3.分式值为 0 的条件:
A=0且 B ≠0
A>0 ,B>0 或 A<0, B<0
A>0 ,B<0 或 A<0 ,B>0
分式 < 0 的条件:
A
B
4.分式 > 0 的条件:
A
B
A
B
形如 ,其中 A ,B 都是整式,
且 B 中含有字母.
1.下列各式(1) (2) (3) (4) (5)
是分式的有 个。
3
2x
3
2x
x
2x2
x
∏
1-
3
2x
2.下列各式中x 取何值时,分式有意义.
X - 1
X + 2
X2 -1
4x
X -1
1
X2 - 2xY+Y?
1
3.下列分式一定有意义的是( )
X+1
x2
X+1
X2+1
X - 1
X2 +1
1
X - 1
练习
3
B
x ≠-2
x≠±1
x ≠±1
x 为一切实数
(1)
(2)
(3)
(4)
A.
B.
C.
D.
4.当x为何值时,分式
(1) 有意义 (2) 值为 0
2x (x-2)
5x (x+2)
5.要使分式 的值为正数,
则x的取值范围是
1-x
-2
X≠0且x≠-2
X=2
X>1
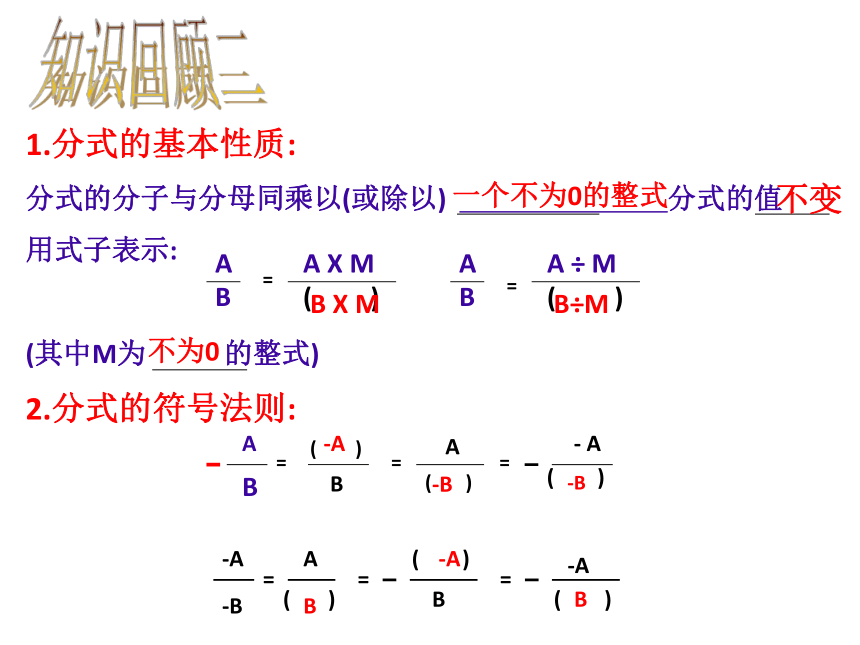
知识回顾二
1.分式的基本性质:
分式的分子与分母同乘以(或除以) 分式的值
用式子表示:
(其中M为 的整式)
A
B
A X M
( )
A
B
A ÷ M
( )
=
=
2.分式的符号法则:
A
B
=
B
( )
=
A
( )
=
- A
( )
-A
-B
=
A
( )
=
B
( )
=
-A
( )
一个不为0的整式
不变
B X M
B÷M
不为0
-A
-B
-B
B
-A
B
【例2】不改变分式的值,把下列分式的分子、分母的首项的符号变为正号.
(1)
(2)
知识回顾三
把分母不相同的几个分式化成分母相同的分式。
关键是找最简公分母:各分母所有因式的最高次幂的积.
1.约分:
2.通分:
把分子、分母的最大公因式(数)约去。
1.约分
(1) (2)
(3)
-6x2y
27xy2
-2(a-b)2
-8(b-a)3
m2+4m+4
m2 - 4
2.通分
(1) (2)
x
6a2b
与
y
9ab2c
a-1
a2+2a+1
与
6
a2-1
约分与通分的依据都是:
分式的基本性质
关键找出分子和分母的公因式
关键找出分母的最简公分母
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母。
分式的乘法法则
用符号语言表达:
两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘。
分式除法法则
用符号语言表达:
知识回顾一
先乘再约分
先把除转化为乘
先因式分解
2/3x2
-2bd/5ac
a-2/a2+a-2
注意:
乘法和除法运算时,结果要化为最简分式 。
分式的加减
同分母相加
异分母相加
通分
知识回顾二
在分式有关的运算中,一般总是先把分子、分母分解因式;
注意:过程中,分子、分母一般保持分解因式的形式。
8、通分(加减运算):
通分
分母不变,分子相加减
解:原式=
整数指数幂有以下运算性质:
(1)am·an=am+n (a≠0)
(2)(am)n=amn (a≠0)
(3)(ab)n=anbn (a,b≠0)
(4)am÷an=am-n (a≠0)
(5) (b≠0)
当a≠0时,a0=1。
(6)
(7)n是正整数时, a-n属于分式。
并且
(a≠0)
知识回顾三
5、整数指数幂:
解:原式=
6、用科学记数法表示:
培优
再见!
分式总复习
第15章分式
复习目标
1.复习分式的定义与基本性质。
2.复习约分、通分的定义和方法。
3.复习分式的运算。
复习指导
认真复习课本127页----142页的内容,注意:
1.对于掌握不太牢固的概念,性质用笔勾画出来。加强记忆。
2.对于有疑问的习题,可请教老师或同学,彻底扫除疑问。
5分钟后,我们进行检测。
分式
分式有意义
分式的值为0
同分母相加减
异分母相加减
概念
的形式
B中含有字母B≠0
分式的加减
分式的乘除
通分
约分
最简分式
同分母相加减
知识回顾一
1.分式的定义:
2.分式有意义的条件:
B≠0
分式无意义的条件:
B = 0
3.分式值为 0 的条件:
A=0且 B ≠0
A>0 ,B>0 或 A<0, B<0
A>0 ,B<0 或 A<0 ,B>0
分式 < 0 的条件:
A
B
4.分式 > 0 的条件:
A
B
A
B
形如 ,其中 A ,B 都是整式,
且 B 中含有字母.
1.下列各式(1) (2) (3) (4) (5)
是分式的有 个。
3
2x
3
2x
x
2x2
x
∏
1-
3
2x
2.下列各式中x 取何值时,分式有意义.
X - 1
X + 2
X2 -1
4x
X -1
1
X2 - 2xY+Y?
1
3.下列分式一定有意义的是( )
X+1
x2
X+1
X2+1
X - 1
X2 +1
1
X - 1
练习
3
B
x ≠-2
x≠±1
x ≠±1
x 为一切实数
(1)
(2)
(3)
(4)
A.
B.
C.
D.
4.当x为何值时,分式
(1) 有意义 (2) 值为 0
2x (x-2)
5x (x+2)
5.要使分式 的值为正数,
则x的取值范围是
1-x
-2
X≠0且x≠-2
X=2
X>1
知识回顾二
1.分式的基本性质:
分式的分子与分母同乘以(或除以) 分式的值
用式子表示:
(其中M为 的整式)
A
B
A X M
( )
A
B
A ÷ M
( )
=
=
2.分式的符号法则:
A
B
=
B
( )
=
A
( )
=
- A
( )
-A
-B
=
A
( )
=
B
( )
=
-A
( )
一个不为0的整式
不变
B X M
B÷M
不为0
-A
-B
-B
B
-A
B
【例2】不改变分式的值,把下列分式的分子、分母的首项的符号变为正号.
(1)
(2)
知识回顾三
把分母不相同的几个分式化成分母相同的分式。
关键是找最简公分母:各分母所有因式的最高次幂的积.
1.约分:
2.通分:
把分子、分母的最大公因式(数)约去。
1.约分
(1) (2)
(3)
-6x2y
27xy2
-2(a-b)2
-8(b-a)3
m2+4m+4
m2 - 4
2.通分
(1) (2)
x
6a2b
与
y
9ab2c
a-1
a2+2a+1
与
6
a2-1
约分与通分的依据都是:
分式的基本性质
关键找出分子和分母的公因式
关键找出分母的最简公分母
两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母。
分式的乘法法则
用符号语言表达:
两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘。
分式除法法则
用符号语言表达:
知识回顾一
先乘再约分
先把除转化为乘
先因式分解
2/3x2
-2bd/5ac
a-2/a2+a-2
注意:
乘法和除法运算时,结果要化为最简分式 。
分式的加减
同分母相加
异分母相加
通分
知识回顾二
在分式有关的运算中,一般总是先把分子、分母分解因式;
注意:过程中,分子、分母一般保持分解因式的形式。
8、通分(加减运算):
通分
分母不变,分子相加减
解:原式=
整数指数幂有以下运算性质:
(1)am·an=am+n (a≠0)
(2)(am)n=amn (a≠0)
(3)(ab)n=anbn (a,b≠0)
(4)am÷an=am-n (a≠0)
(5) (b≠0)
当a≠0时,a0=1。
(6)
(7)n是正整数时, a-n属于分式。
并且
(a≠0)
知识回顾三
5、整数指数幂:
解:原式=
6、用科学记数法表示:
培优
再见!
