人教A版高中数学必修4课件:2.3平面向量的基本定理及坐标表示(2.3.1-2.3.4) 课件(共32张PPT)
文档属性
| 名称 | 人教A版高中数学必修4课件:2.3平面向量的基本定理及坐标表示(2.3.1-2.3.4) 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 15:43:02 | ||
图片预览





文档简介
(共32张PPT)
2.3平面向量的基本定理及坐标表示
复习:共线向量基本定理:
O
C
A
B
M
N
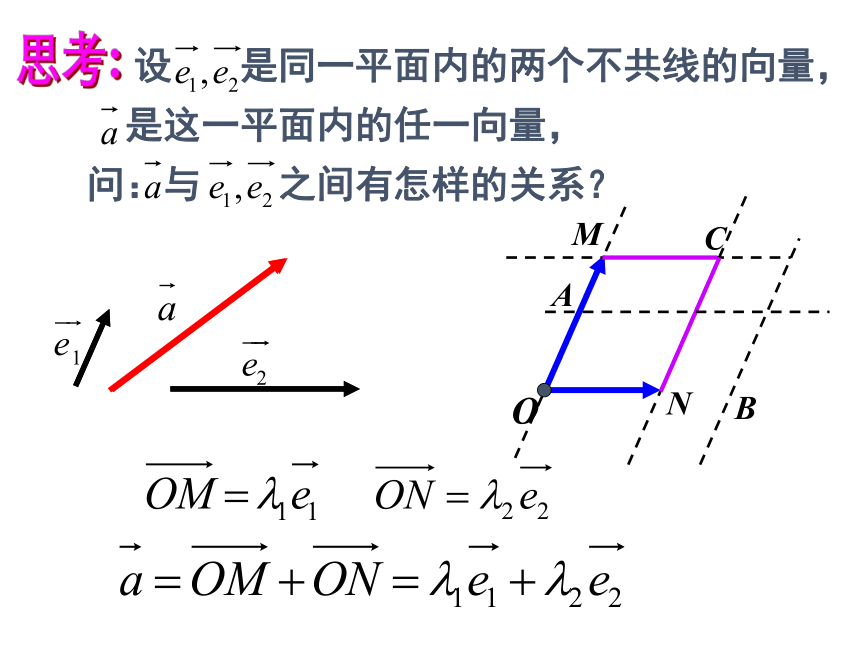
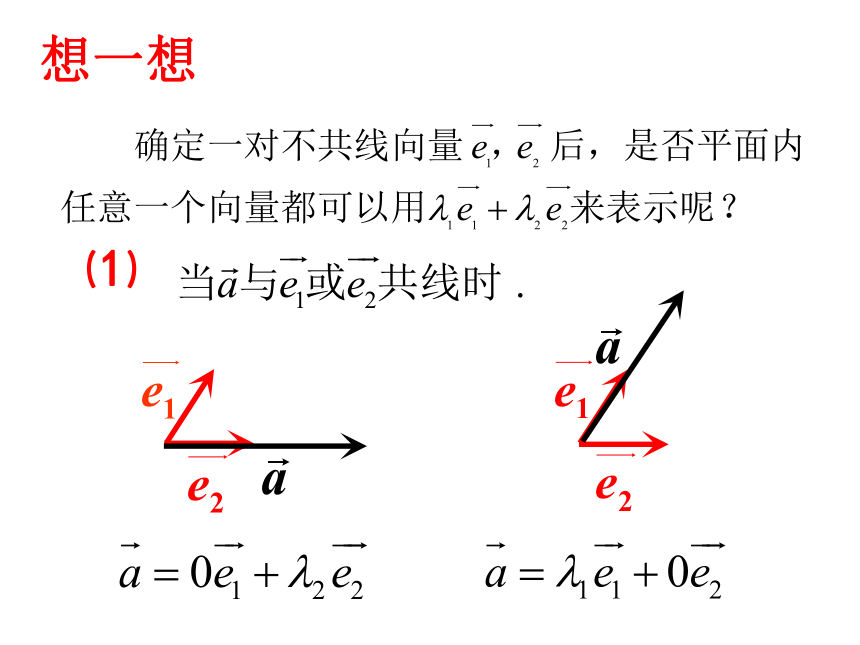
想一想
⑴
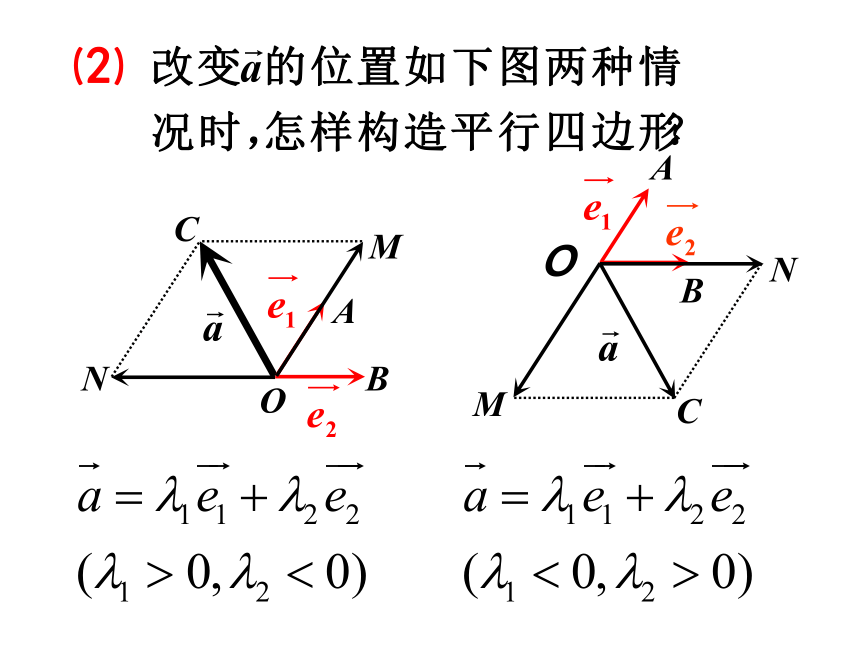
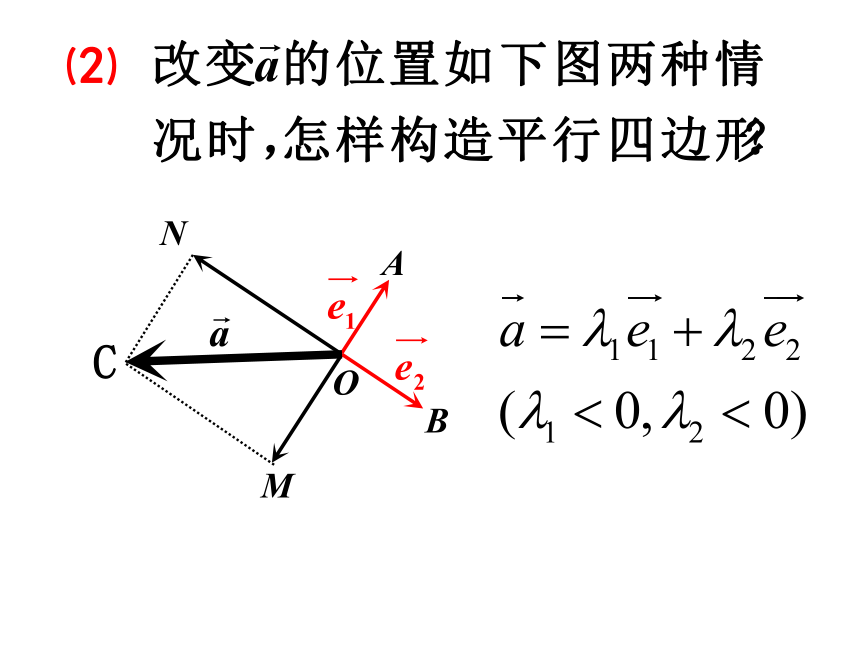
⑵
⑵
C
一、平面向量基本定理:
2、基底不唯一,关键是不共线.
4、基底给定时,分解形式唯一.
练习:下列说法是否正确?
1.在平面内只有一对基底.
2.在平面内有无数对基底.
3.零向量不可作为基底.
4.平面内不共线的任意一
对向量,都可作为基底.
×
√
√
√
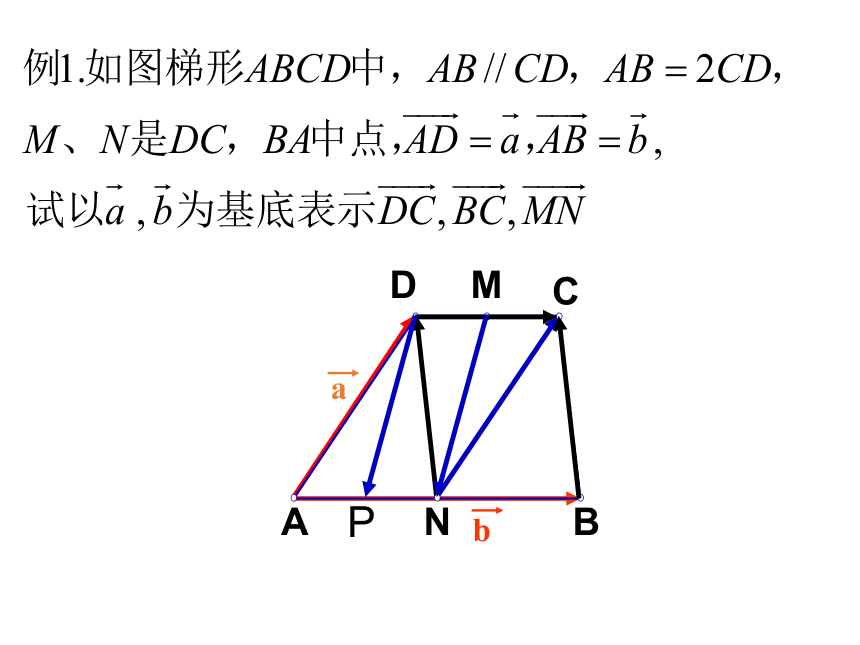
A
B
D
C
N
M
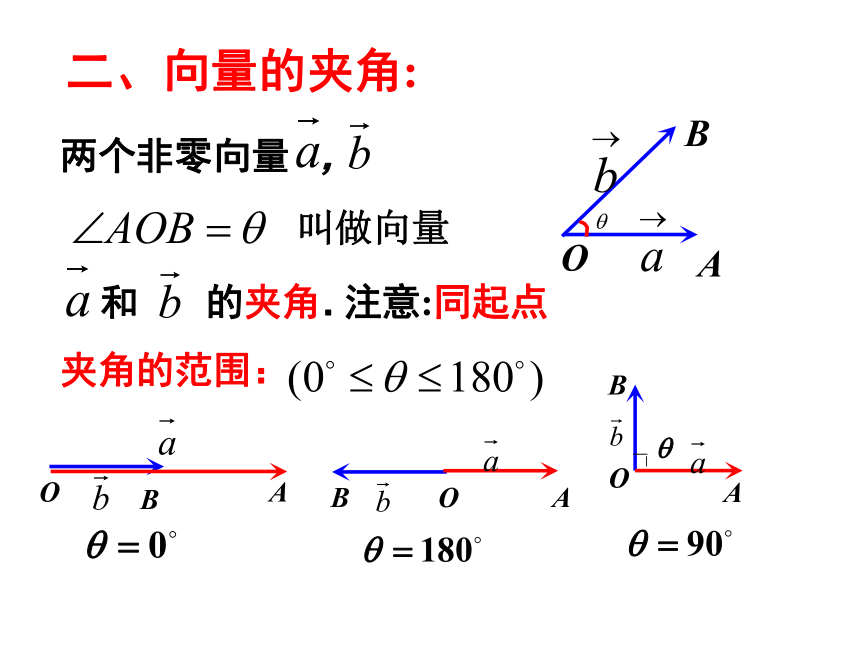
二、向量的夹角:
两个非零向量 ,
和 的夹角.
夹角的范围:
注意:同起点
叫做向量
注意:同起点
O
一个重要结论
结论:
2.3.2平面向量正交分解及坐标表示
思考?
在平面直角坐标系中:
2.2.3平面向量的正角分解及坐标表示.
向量的
正交分解
物理背景:
y
O
x
(x,y)叫做向量 的
坐标,记作
正交单位基底
平面向量的正角分解及坐标表示.
O
x
y
A
当向量的起点在坐标原点时,向量的坐标就是向量终点的坐标.
坐标(x,y)
两个向量相等,利用坐标如何表示?
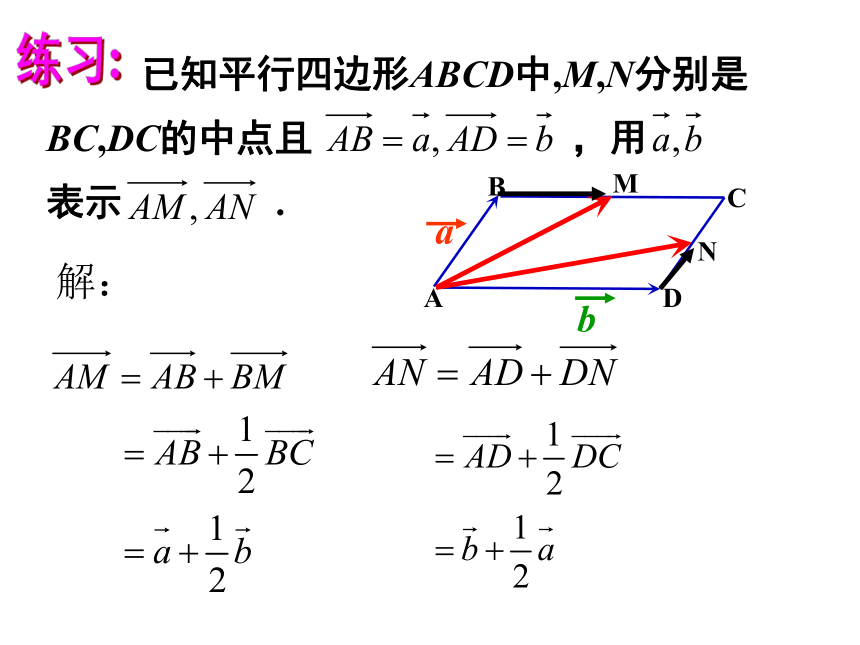
解:
j
y
x
O
i
a
A1
A
A2
B
2.3.3 平面向量的坐标运算
(1)如何进行平面向量的坐标运算?
(2)与数的坐标运算是否有一定的关系?
下面我们探究向量的坐标运算法则:
x
y
O
有向线段的终点的坐标减去起点的坐标.
解:
x
C(3,4)
B(-1,3)
A(-2,1)
D
D(x,y)
例5:三角形、平行四边形法则
x
C(3,4)
B(-1,3)
A(-2,1)
D(x,y)
O
思考:如何用坐标来表示两个
向量的共线关系呢?
2.3.4 平面向量共线的坐标表示
共线向量的坐标关系
例6、已知a=(4,2),b=(6,y)
且a//b ,求y的值。
所以A、B、C三点共线。
例8已知如图,求P点的坐标.
小结
1.平面向量基本定理:
2.向量的夹角:
3.平面向量的坐标表示:
4.一个重要结论:
作业:
1.预习教材107页的相关内容
2.教材第102页第1,2,3,4题
3.试卷 2.3(1-2)平面向量的基本
定理及坐标表示。
本课件共有四课时的内容,因此根据本课的实际确定小结与作业.
2.3平面向量的基本定理及坐标表示
复习:共线向量基本定理:
O
C
A
B
M
N
想一想
⑴
⑵
⑵
C
一、平面向量基本定理:
2、基底不唯一,关键是不共线.
4、基底给定时,分解形式唯一.
练习:下列说法是否正确?
1.在平面内只有一对基底.
2.在平面内有无数对基底.
3.零向量不可作为基底.
4.平面内不共线的任意一
对向量,都可作为基底.
×
√
√
√
A
B
D
C
N
M
二、向量的夹角:
两个非零向量 ,
和 的夹角.
夹角的范围:
注意:同起点
叫做向量
注意:同起点
O
一个重要结论
结论:
2.3.2平面向量正交分解及坐标表示
思考?
在平面直角坐标系中:
2.2.3平面向量的正角分解及坐标表示.
向量的
正交分解
物理背景:
y
O
x
(x,y)叫做向量 的
坐标,记作
正交单位基底
平面向量的正角分解及坐标表示.
O
x
y
A
当向量的起点在坐标原点时,向量的坐标就是向量终点的坐标.
坐标(x,y)
两个向量相等,利用坐标如何表示?
解:
j
y
x
O
i
a
A1
A
A2
B
2.3.3 平面向量的坐标运算
(1)如何进行平面向量的坐标运算?
(2)与数的坐标运算是否有一定的关系?
下面我们探究向量的坐标运算法则:
x
y
O
有向线段的终点的坐标减去起点的坐标.
解:
x
C(3,4)
B(-1,3)
A(-2,1)
D
D(x,y)
例5:三角形、平行四边形法则
x
C(3,4)
B(-1,3)
A(-2,1)
D(x,y)
O
思考:如何用坐标来表示两个
向量的共线关系呢?
2.3.4 平面向量共线的坐标表示
共线向量的坐标关系
例6、已知a=(4,2),b=(6,y)
且a//b ,求y的值。
所以A、B、C三点共线。
例8已知如图,求P点的坐标.
小结
1.平面向量基本定理:
2.向量的夹角:
3.平面向量的坐标表示:
4.一个重要结论:
作业:
1.预习教材107页的相关内容
2.教材第102页第1,2,3,4题
3.试卷 2.3(1-2)平面向量的基本
定理及坐标表示。
本课件共有四课时的内容,因此根据本课的实际确定小结与作业.
