高中数学人教A版必修三教案3.3.2均匀随机数的产生
文档属性
| 名称 | 高中数学人教A版必修三教案3.3.2均匀随机数的产生 |  | |
| 格式 | zip | ||
| 文件大小 | 638.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 15:41:08 | ||
图片预览




文档简介
课时首页 第 页
授课题目 3.2.2均匀随机数的产生 授课时间 年 月 日
本课时知识点及其核心素养要求 通过模拟试验,感知应用数学解决问题的方法,了解均匀随机数的概念;掌握利用计算器(计算机)产生均匀随机数的方法;自觉养成动手、动脑的良好习惯。会利用均匀随机数解决具体的有关概率的问题,理解随机模拟的基本思想是用频率估计概率,学习时养成勤学严谨的学习习惯,提升逻辑思维能力和探索创新能力 核心素养:数学运算 逻辑推理 数据分析
教学重点和难点教学重点:掌握【0,1】上均匀随机数的产生及【a,b】上均匀随机数的产生,学会采用适当的随机模拟法去估计几何概率。 教学难点:利用计算器或计算机产生均匀随机数并运用到概率的实际应用中。
板书设计3.2.2均匀随机数的产生
教学流程 第 页
根据《课标》或《考纲》要求解析知识点(点)的内涵 根据核心素养要求和学生学情设 计 教 学 过 程
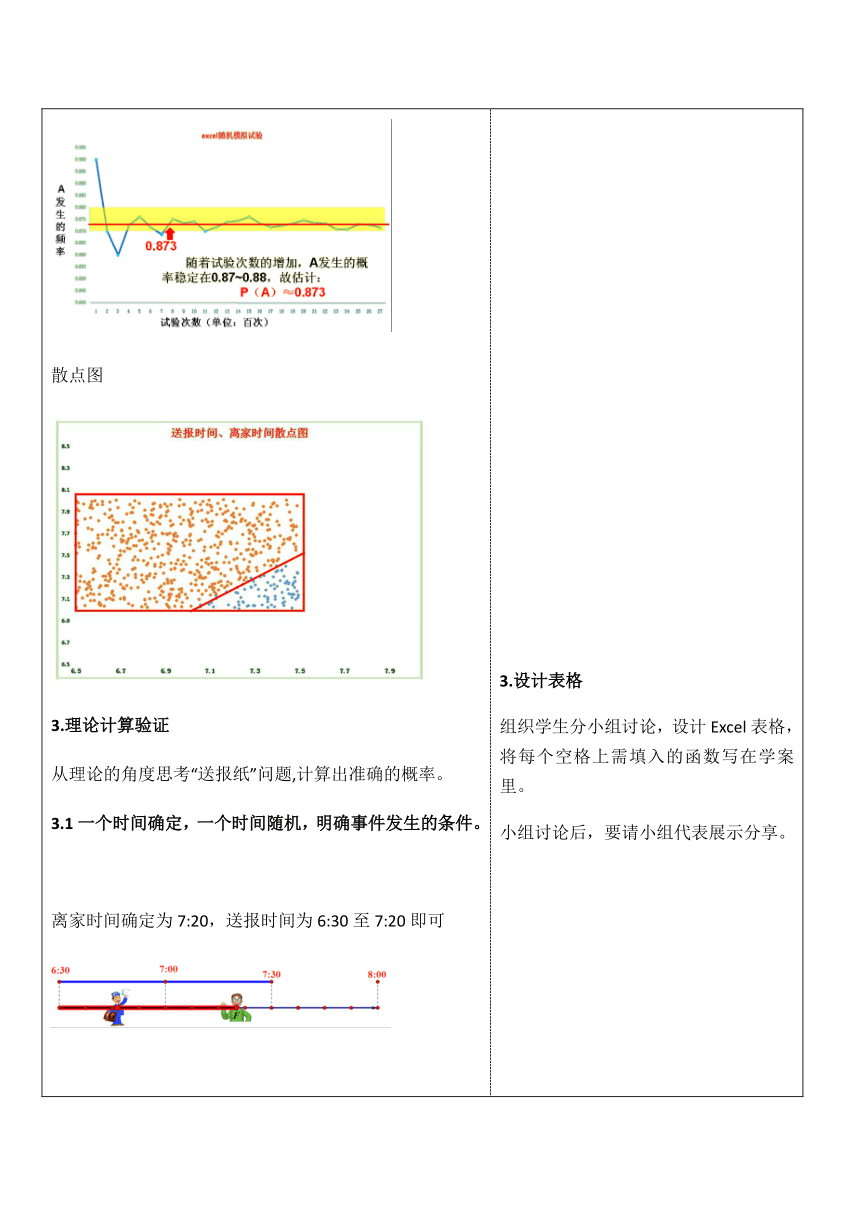
一、原理引入随机模拟试验:试验结果——随机数古典概型: 离散有限的试验结果——整数值随机数几何概型: 连续无限的试验结果——均匀随机数讲均匀随机数的产生基础:如何产生[0,1]均匀随机数计算器:SHIFT RAN# = ,反复按 = Excel表格:空格中输入函数“=rand()”,再回车特殊:如何产生[2,5]均匀随机数x是区间[0,1]的均匀随机数,2+3x为区间[2,5]的均匀随机数一般化:如何产生[a,b]均匀随机数x是区间[0,1]的均匀随机数,a+(b-a)x为区间[a,b]的均匀随机数演示:用计算器和Excel表格演示产生[0,1]的均匀随机数。问1:在已经产生[0,1]之间的均匀随机数的基础上如何得到[2,5]之间的均匀随机数?请同学回答问2:问题一般化,要产生任意指定区间[a,b]上的均匀随机数可以如何变换呢? 活动:学生动手操作,产生10个[2,5]之间的均匀随机数,并记录在学案上。二、典例探究问题引入及解析例2:假设你家订了一份报纸,邮递员可能在早上6:30-7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00-8:00之间,问你父亲在离开家前能得到报纸(称为事件A)的概率是多少? 2.“Excel表格”模拟试验Excel试验原理:用Excel表格中的函数来实现均匀随机数的产生和数据的统计和计算。问题导引:●为了表示时间,我们需要产生几组均匀随机数,范围是什么? ●事件发生的条件是什么?如何用数学语言表示?●如何统计事件发生的频数?如何计算频率?表格设计:实践操作:散点图3.理论计算验证从理论的角度思考“送报纸”问题,计算出准确的概率。3.1一个时间确定,一个时间随机,明确事件发生的条件。离家时间确定为7:20,送报时间为6:30至7:20即可 送报时间确定为7:15,送报时间为7:15至8:00即可 A发生的条件是送报时间≤离家时间。3.2.两个时间均随机,确定概率模型 3.3设量建系,量化面积,计算概率 邮递员送报纸时间为x, 则,爸爸离家时间为y,则,爸爸离家前取得报纸, 只需送报时间早于离家时间,则 :3.4结论分析4.模拟思路总结例2送报纸问题模拟什么?送报时间,离家时间用什么模拟?两组均匀随机数x 、y随机数的范围? 事件发生的条件?随机模拟试验的工具Excel表格拓展应用问题转化例3 在图3.3-3的正方形中随机撒一把豆子,用随机模拟的方法估计圆周率的值。思路类比类比例2试验设计思路,通过回答表格中的问题,形成试验的雏形。 例3圆周率的估计问题模拟什么?豆子落点用什么模拟?建系后,用两组x、y均匀随机数构成横纵坐标。随机数的范围?事件发生的条件?随机模拟试验的工具Excel表格类比例2的Excel表格,初步设置例3的Excel表格课后实践任务:思考每个空格填入的函数,完成Excel表格的设计,并将按表格的设置,实践操作,估计出圆周率的值课堂小结 生:复习概率的定义,回顾古典概型中,整数值随机数的产生方法,理解为什么要学习均匀随机数的产生教师讲授:解释学习均匀随机数产生方法的必要性及均匀随机数的特点 演示:用计算器和Excel表格演示产生[0,1]的均匀随机数。问1:在已经产生[0,1]之间的均匀随机数的基础上如何得到[2,5]之间的均匀随机数?请同学回答问2:问题一般化,要产生任意指定区间b]上的均匀随机数可以如何变换呢? 活动:学生动手操作,产生10个[2,5]之间的均匀随机数,并记录在学案上。 老师通过自制教具转盘演示,解释题意,简单解析通过转表盘来设计随机模拟试验,提出通过手动转表盘能否完成大量重复试验的疑惑,从而引出通过计算机自动生成数据的必要性。 Excel试验原理讲授:用函数来实现均匀随机数的产生和数据的统计和计算,估计的过程更为科学和高效。 2.问题导引:引导学生思考3个问题,为设计随机模拟试验提供线索 3.设计表格组织学生分小组讨论,设计Excel表格,将每个空格上需填入的函数写在学案里。小组讨论后,要请小组代表展示分享。 4.实践操作请同学们将设计好的内容输入Excel表格中,快速得到试验的结果,最后我们来比比看,哪个小组估计的概率最准确。 学生实践后报出试验结果,老师演示实践过程:以试验的次数设为横轴,A发生的频率为纵轴,形成折线图,随机取其中一个折线图观察,试验次数越多,频率会稳定在0.87~0.88之间,于是最后取常数0.873作为试验的结果。 到底哪个结果更准确呢?再看以送报时间和离家时间构成的散点图,满足条件的点为红色,不满足条件的的点为蓝色。发现所有的点分布在一个矩形内,红色点和蓝色点之间有一条明显的界限,这个现象说明什么? 3.2确定模型几何画板演示:分离两个时间轴,几何画板动态分析事件结果构成方形区域,确定问题为面积型的几何概型。 3.3量化计算组织学生分小组活动,引导学生通过建立直角坐标系来解决问题。最后师生一起完成量化计算,得到准确概率。 3.4结论分析讲授:将试验得到的散点图和估计的概率,与理论画出的示意图和计算的概率相对比,会发现这惊人的相似其实是一个必然,充分验证了随机模拟试验结果的可靠性。哪个小组的数据最准确?答案自然揭晓了! 问:先思考,假设正方形的边长为2 ,在正方形中随机撒一把豆子,豆子落在圆内的概率是多少?讲授:故要估计圆周率的值,实为估计豆子落在圆内的概率。 师生互动,老师围绕例2提炼出的主要问题提问,让学生类比运用,独立思考设计随机模拟试验,并最后落实Excel表格的设计上。 安排学生课后完成实践操作任务 引导学生归纳课堂学习内容,突出本课核心思想
课时尾页 第 页
达标检测设计把【0,1】上的均匀随机数转化为【-2,6】上的均匀随机数,需要实施的变换为A.y=x×8 B.y=x×8+2 C.y=.x×8-2 D.y=.x×8+62、设A为圆周上一点,在圆周上等可能地任取一点与A连接,则弦长超过半径的倍的概率是
作业设计
教学反思
