5.4 有理数的加法 课件(17张PPT)
文档属性
| 名称 | 5.4 有理数的加法 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 185.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
复习
(符号、绝对值)
3、小学里学过什么数的加法运算?
(正数及零的加法运算)
1、求下列各数的绝对值.
2、一个不等于0的有理数可看作由哪两
部分组成?
上半年
下半年
合计
第一年
1.2
0.8
第二年
-0.6
-0.7
第三年
-0.5
0.5
第四年
0.9
-0.1
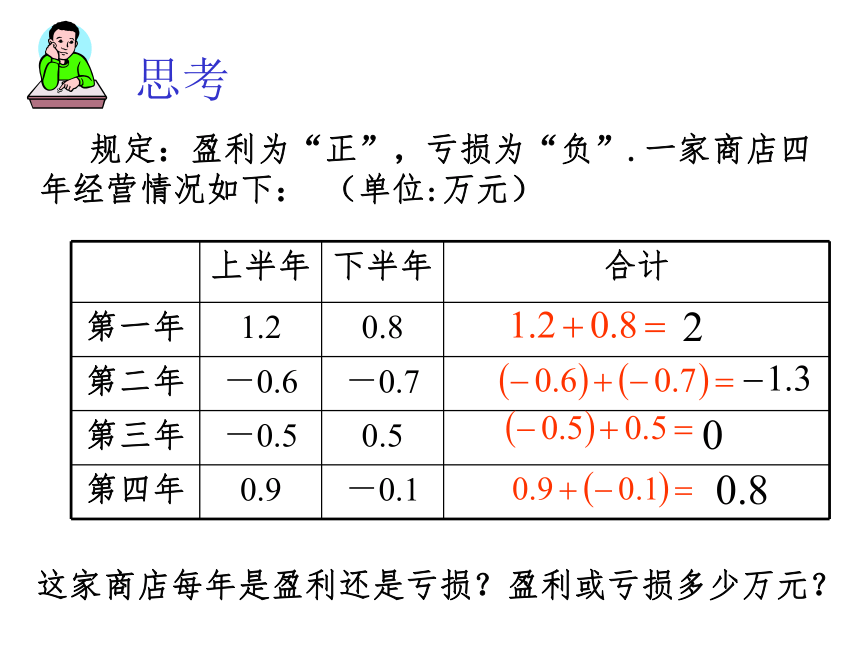
规定:盈利为“正”,亏损为“负”.一家商店四年经营情况如下:
(单位:万元)
思考
这家商店每年是盈利还是亏损?盈利或亏损多少万元?
有理数加法法则
5.4
有理数的加法
一个数同零相加,仍得这个数。
同号两数相加,取原来的符号,并把绝对值相加。
异号两数相加,绝对值相等时和为零;绝对值不相等时,其和的绝对值为较大的绝对值减去较小的绝对值所得的差,其和的符号取绝对值较大的加数的符号.
解
(把绝对值相加)
(同号两数相加)
例题1
计算
(
)
(取原来的符号)
先定符号,
再定绝对值
(绝对值不相等的
异号两数相加)
(取绝对值较大的加数符号)
(用较大的绝对值减去较小的绝对值)
(
)
先定符号,
再定绝对值
解
计算:
解
1.有理数加法分三类:
,
,
;
同号相加
异号相加
数与0相加
符号
绝对值
归纳小结:
2.有理数加法法则
有理数加法运算须确定:
和的
与和的
;
3、一个数同
相加,仍得这个数。
1、同号两数相加,取
符号,并把
相加。例如
。
2、异号两数相加,绝对值相等时其和为
;例如
。
绝对值不相等时,其和的绝对值为较大的绝对值
较小的绝对值所得的差,其和的符号取
的符号.例如
。
填
空:
原来的
绝对值
零
减去
绝对值较大的加数
零
思考
以下两个算式有什么特点,其计算结果是否相等
加法交换律:
两个有理数相加,交换加数的位置,和不变。
三个有理数相加,先把前两个数相加,或者先把后两个数相加,和不变。
加法结合律:
以下两个算式有什么特点,其计算结果是否相等
有理数加法的运算律
交换律:
结合律:
两个有理数相加,交换加数的位置,和不变。
三个有理数相加,先把前两个数相加,或者先把后两个数相加,和不变。
例题1
计算
解
同号两数先相加
(交换律)
(结合律)
有分母相同的,先把同分母的数相加.
有相反数的先把相反数相加,能凑整的先凑整.
例题2
已知一辆运货卡车从A站出发,先向东行驶15千米,卸货后再向西行驶25千米装上另一批货物,然后又向东行驶20千米后停下来,问卡车最后停在何处.
解
设向东为正
东
西
15
25
20
答:卡车停在A站向东10千米处.
(千米)
小结:
1.有理数的加法交换律、结合律可以
简化计算.
2、技能要求:
⑴
同号的加数放在一起先相加.
⑵
和为0的加数放在一起先相加.
⑶
和为整数的加数放在一起先相加.
复习
(符号、绝对值)
3、小学里学过什么数的加法运算?
(正数及零的加法运算)
1、求下列各数的绝对值.
2、一个不等于0的有理数可看作由哪两
部分组成?
上半年
下半年
合计
第一年
1.2
0.8
第二年
-0.6
-0.7
第三年
-0.5
0.5
第四年
0.9
-0.1
规定:盈利为“正”,亏损为“负”.一家商店四年经营情况如下:
(单位:万元)
思考
这家商店每年是盈利还是亏损?盈利或亏损多少万元?
有理数加法法则
5.4
有理数的加法
一个数同零相加,仍得这个数。
同号两数相加,取原来的符号,并把绝对值相加。
异号两数相加,绝对值相等时和为零;绝对值不相等时,其和的绝对值为较大的绝对值减去较小的绝对值所得的差,其和的符号取绝对值较大的加数的符号.
解
(把绝对值相加)
(同号两数相加)
例题1
计算
(
)
(取原来的符号)
先定符号,
再定绝对值
(绝对值不相等的
异号两数相加)
(取绝对值较大的加数符号)
(用较大的绝对值减去较小的绝对值)
(
)
先定符号,
再定绝对值
解
计算:
解
1.有理数加法分三类:
,
,
;
同号相加
异号相加
数与0相加
符号
绝对值
归纳小结:
2.有理数加法法则
有理数加法运算须确定:
和的
与和的
;
3、一个数同
相加,仍得这个数。
1、同号两数相加,取
符号,并把
相加。例如
。
2、异号两数相加,绝对值相等时其和为
;例如
。
绝对值不相等时,其和的绝对值为较大的绝对值
较小的绝对值所得的差,其和的符号取
的符号.例如
。
填
空:
原来的
绝对值
零
减去
绝对值较大的加数
零
思考
以下两个算式有什么特点,其计算结果是否相等
加法交换律:
两个有理数相加,交换加数的位置,和不变。
三个有理数相加,先把前两个数相加,或者先把后两个数相加,和不变。
加法结合律:
以下两个算式有什么特点,其计算结果是否相等
有理数加法的运算律
交换律:
结合律:
两个有理数相加,交换加数的位置,和不变。
三个有理数相加,先把前两个数相加,或者先把后两个数相加,和不变。
例题1
计算
解
同号两数先相加
(交换律)
(结合律)
有分母相同的,先把同分母的数相加.
有相反数的先把相反数相加,能凑整的先凑整.
例题2
已知一辆运货卡车从A站出发,先向东行驶15千米,卸货后再向西行驶25千米装上另一批货物,然后又向东行驶20千米后停下来,问卡车最后停在何处.
解
设向东为正
东
西
15
25
20
答:卡车停在A站向东10千米处.
(千米)
小结:
1.有理数的加法交换律、结合律可以
简化计算.
2、技能要求:
⑴
同号的加数放在一起先相加.
⑵
和为0的加数放在一起先相加.
⑶
和为整数的加数放在一起先相加.
