苏科版九年级数学上册第二章对称图形——圆:动点与动圆综合 复习(含答案)
文档属性
| 名称 | 苏科版九年级数学上册第二章对称图形——圆:动点与动圆综合 复习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 414.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-27 20:10:21 | ||
图片预览




文档简介
初三数学动圆中的几何
学员姓名 年 级 初三 上课时间
辅导科目 数学 学科教师
课 题 与圆有关的动点问题
动点与动圆问题解题技巧:
1.找到动态过程中不变的量,利用或探索(比如相似)已知条件列等式求值;
2.画出临界情况或符合题目情形的草图(非常重要),根据图像找等量关系。
动圆与几何图形结合问题
例1.如图,在中,,点从点出发,在边上以的速度向点运动,与此同时,点从点出发,在边上以的速度向点运动,过的中点作的垂线,则当点运动了 时,以点为圆心,为半径的圆与直线相切.
例2.如图,在中,,动点从点出发,在边上以每秒的速度向点匀速运动,同时动点也从点出发,沿以每秒的速度匀速运动,运动时间为秒,连接,以为直径作.
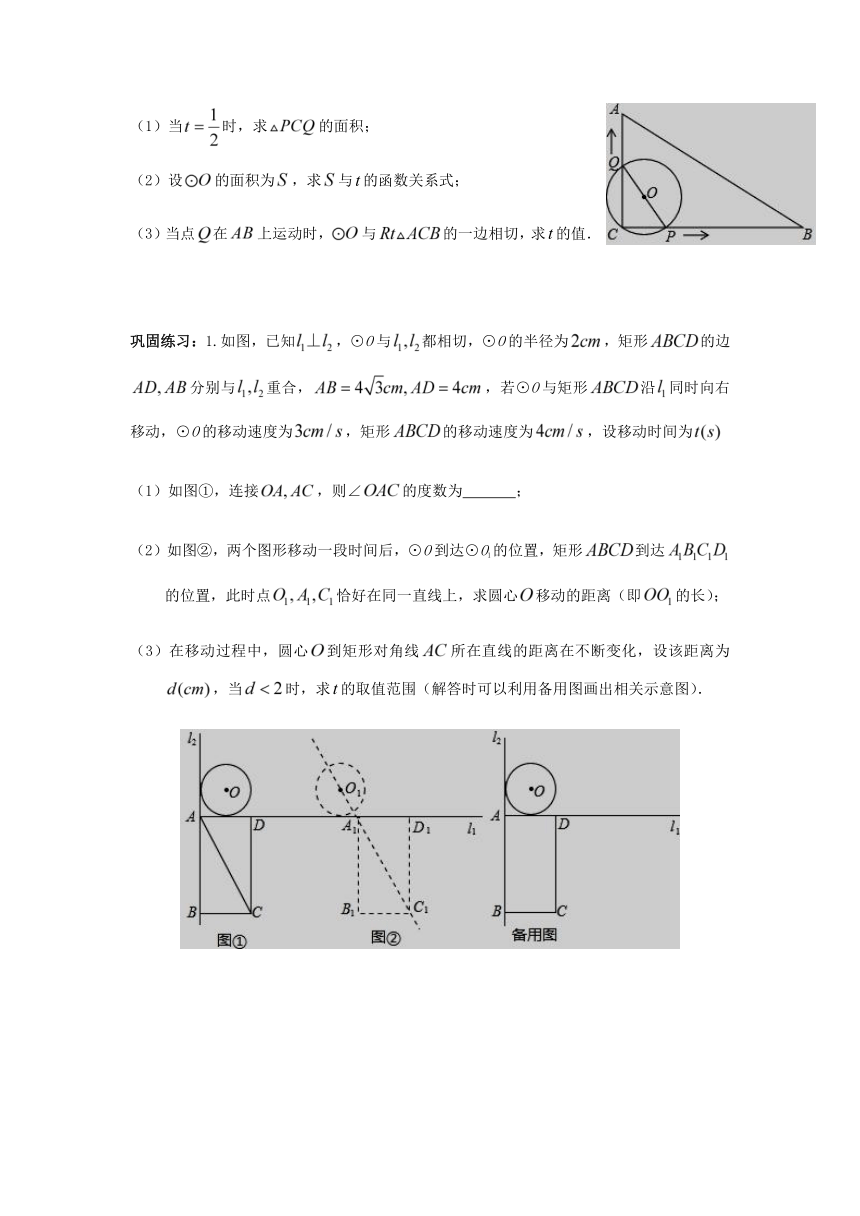
(1)当时,求的面积;
(2)设的面积为,求与的函数关系式;
(3)当点在上运动时,与的一边相切,求的值.
巩固练习:1.如图,已知,⊙O与都相切,⊙O的半径为,矩形的边分别与重合,,若⊙O与矩形沿同时向右移动,⊙O的移动速度为,矩形的移动速度为,设移动时间为
(1)如图①,连接,则∠的度数为 ;
(2)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形到达的位置,此时点恰好在同一直线上,求圆心移动的距离(即的长);
(3)在移动过程中,圆心到矩形对角线所在直线的距离在不断变化,设该距离为,当时,求的取值范围(解答时可以利用备用图画出相关示意图).
动态一次函数与圆
例3.如图,平面直角坐标系xOy中,一次函数(b为常数,b>0)的图象与x轴、y轴分别相交于点A、B,半径为4的⊙O与x轴正半轴相交于点C,与y轴相交于点D、E,点D在点E上方.
(1)若直线AB与有两个交点F、G.
①求∠CFE的度数;
②用含b的代数式表示FG2,并直接写出b的取值范围;
(2)设b≥5,在线段AB上是否存在点P,使∠CPE=45°?若存在,请求出P点坐标;若不存在,请说明理由.
巩固练习:如图,在平面直角坐标系中,直线AB与轴,轴分别交于点,动点P从点O出发,沿轴负方向以每秒1个单位的速度运动,同时动点Q从点B出发,沿射线BO方向以每秒2个单位的速度运动,过点P作PC⊥AB于点C,连接PQ,CQ,以PQ,CQ为邻边构造平行四边形PQCD,设点P运动的时间为t秒.
(1)当点Q在线段OB上时,用含t的代数式表示PC,AC的长;
(2)在运动过程中.
①当点D落在轴上时,求出满足条件的t的值;
②若点D落在△ABO内部(不包括边界)时,直接写出t的取值范围;
(3)作点Q关于x轴的对称点Q′,连接CQ′,在运动过程中,是否存在某时刻使过A,P,C三点的圆与△CQQ′三边中的一条边相切?若存在,请求出t的值;若不存在,请说明理由.
课 后 作 业
1.如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.
(1)求BF的长(用含有t的代数式表示),并求出t的取值范围;
(2)当t为何值时,线段EN与⊙M相切?
(3)若⊙M与线段EN只有一个公共点,求t的取值范围.
2.如图,已知Rt△ABC的直角边AC与Rt△DEF的直角边DF在同一条直线上,且AC=60c,BC=45cm,DF=6cm,EF=8cm.现将点C与点F重合,再以4cm/s的速度沿CA方向移动△DEF;同时,点P从点A出发,以5cm/s的速度沿AB方向移动.设移动时间为t(s),以点P为圆心,3t(cm)长为半径的⊙P与AB相交于点M,N,当点F与点A重合时,△DEF与点P同时停止移动,在移动过程中,
(1)连接ME,当ME∥AC时,t= s;
(2)连接NF,当NF平分DE时,求t的值;
(3)是否存在⊙P与Rt△DEF的两条直角边所在的直线同时相切的时刻?若存在,求出t的值;若不存在,说明理由.
3.如图,矩形ABCD的边AB=3cm,AD=4cm,点E从点A出发,沿射线AD移动,以CE为直径作圆O,点F为圆O与射线BD的公共点,连接EF、CF,过点E作EG⊥EF,EG与圆O相交于点G,连接CG.
(1)试说明四边形EFCG是矩形;
(2)当圆O与射线BD相切时,点E停止移动,在点E移动的过程中,
①矩形EFCG的面积是否存在最大值或最小值?若存在,求出这个最大值或最小值;若不存在,说明理由;
②求点G移动路线的长.
参 考 答 案
例1.
例2.(1);(2);(3)
巩固练习:
解:(1)∵l1⊥l2,⊙O与l1,l2都相切,∴∠OAD=45°,∵AB=4cm,AD=4cm,∴CD=4cm,AD=4cm,∴tan∠DAC===,∴∠DAC=60°,∴∠OAC的度数为:∠OAD+∠DAC=105°,故答案为:105;(2)如图位置二,当O1,A1,C1恰好在同一直线上时,设⊙O1与l1的切点为E,连接O1E,可得O1E=2,O1E⊥l1,在Rt△A1D1C1中,∵A1D1=4,C1D1=4,∴tan∠C1A1D1=,∴∠C1A1D1=60°,在Rt△A1O1E中,∠O1A1E=∠C1A1D1=60°,∴A1E==,∵A1E=AA1﹣OO1﹣2=t﹣2,∴t﹣2=,∴t=+2,∴OO1=3t=2+6;(3)①当直线AC与⊙O第一次相切时,设移动时间为t1,如图,此时⊙O移动到⊙O2的位置,矩形ABCD移动到A2B2C2D2的位置,设⊙O2与直线l1,A2C2分别相切于点F,G,连接O2F,O2G,O2A2,∴O2F⊥l1,O2G⊥A2G2,由(2)得,∠C2A2D2=60°,∴∠GA2F=120°,∴∠O2A2F=60°,在Rt△A2O2F中,O2F=2,∴A2F=,∵OO2=3t,AF=AA2+A2F=4t1+,∴4t1+﹣3t1=2,∴t1=2﹣,②当直线AC与⊙O第二次相切时,设移动时间为t2,记第一次相切时为位置一,点O1,A1,C1共线时位置二,第二次相切时为位置三,由题意知,从位置一到位置二所用时间与位置二到位置三所用时间相等,∴+2﹣(2﹣)=t2﹣(+2),解得:t2=2+2,综上所述,当d<2时,t的取值范围是:2﹣<t<2+2.
例3.解:(1)连接CD,EA,∵DE是直径,∴∠DCE=90°,∵CO⊥DE,且DO=EO,
∴∠ODC=OEC=45°,∴∠CFE=∠ODC=45°,
(2)①如图,作OM⊥AB点M,连接OF,
∵OM⊥AB,直线的函数式为:y=﹣x+b,∴OM所在的直线函数式为:y=x,
∴交点M(b,b)∴OM2=(b)2+(b)2,
∵OF=4,∴FM2=OF2﹣OM2=42﹣(b)2﹣(b)2,
∵FM=FG,
∴FG2=4FM2=4×[42﹣(b)2﹣(b)2]=64﹣b2=64×(1﹣b2),∵直线AB与有两个交点F、G.∴4≤b<5,
(3)如图,
当b=5时,直线与圆相切,∵DE是直径,
∴∠DCE=90°,∵CO⊥DE,且DO=EO,
∴∠ODC=OEC=45°,∴∠CFE=∠ODC=45°,
∴存在点P,使∠CPE=45°,
连接OP,∵P是切点,∴OP⊥AB,
∴OP所在的直线为:y=x,又∵AB所在的直线为:y=﹣x+5,
∴P(,).
巩固练习:(1);(2) ;(3)
课后作业:1.(1);(2);(3)
2.(1);(2);(3)
3.解:(1)证明:∵CE为⊙O的直径,∴∠CFE=∠CGE=90°.
∵EG⊥EF,∴∠FEG=90°.∴∠CFE=∠CGE=∠FEG=90°.∴四边形EFCG是矩形.
(2)①存在.连接OD,∵四边形ABCD是矩形,∴∠A=∠ADC=90°.
∵点O是CE的中点,∴OD=OC.∴点D在⊙O上.
∵∠FCE=∠FDE,∠A=∠CFE=90°,∴△CFE∽△DAB.∴=()2.
∵AD=4,AB=3,∴BD=5,S△CFE=()2?S△DAB=××3×4=.
∴S矩形ABCD=2S△CFE=.
∵四边形EFCG是矩形,∴FC∥EG.∴∠FCE=∠CEG.
∵∠GDC=∠CEG,∠FCE=∠FDE,∴∠GDC=∠FDE.
∵∠FDE+∠CDB=90°,∴∠GDC+∠CDB=90°.∴∠GDB=90°
Ⅰ.当点E在点A(E′)处时,点F在点B(F′)处,点G在点D(G′处,如图2①所示.此时,CF=CB=4.
Ⅱ.当点F在点D(F″)处时,直径F″G″⊥BD,
此时⊙O与射线BD相切,CF=CD=3.
Ⅲ.当CF⊥BD时,CF最小,此时点F到达F″′,
S△BCD=BC?CD=BD?CF″′.∴4×3=5×CF″′.∴CF″′=.∴≤CF≤4.
∵S矩形ABCD=,∴×()2≤S矩形ABCD≤×42.∴≤S矩形ABCD≤12.
∴矩形EFCG的面积最大值为12,最小值为.
②∵∠GDC=∠FDE=定值,点G的起点为D,终点为G″,∴点G的移动路线是线段DG″.∵∠GDC=∠FDE,∠DCG″=∠A=90°,∴△DCG″∽△DAB.
∴=.∴=.∴DG″=.∴点G移动路线的长为.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
